s2Eva_IIT2011_T3 EDP Parabólica, explícito

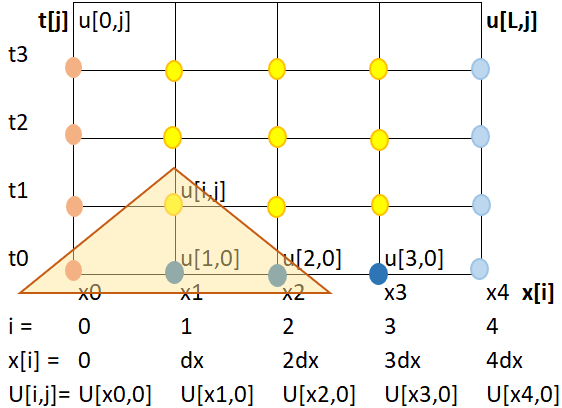
Ejercicio: 2Eva_IIT2011_T3 EDP Parabólica, explícito

La ecuación a resolver es:

\frac{\delta u}{\delta t} - \frac{\delta^2 u}{\delta x^2} =2

Como el método requerido es explícito se usan las diferencias divididas:

\frac{d^2 u}{dx^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} \frac{du}{dt} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t}

Reordenando la ecuación al modelo realizado en clase:

\frac{\delta^2 u}{\delta x^2} = \frac{\delta u}{\delta t} - 2 \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t} - 2

multiplicando cada lado por Δt

\frac{\Delta t}{(\Delta x)^2} \Big[u_{i+1,j} - 2 u_{i,j} + u_{i-1,j} \Big]= u_{i,j+1} - u_{i,j} - 2\Delta t

Se establece el valor de

\lambda = \frac{\Delta t}{(\Delta x)^2} \lambda u_{i+1,j} - 2 \lambda u_{i,j} + \lambda u_{i-1,j} = u_{i,j+1} - u_{i,j} - 2\Delta t

obteniendo la ecuación general, ordenada por índices de izquierda a derecha:

\lambda u_{i-1,j} +(1- 2 \lambda)u_{i,j} + \lambda u_{i+1,j} + 2\Delta t = u_{i,j+1}

con valores de:

λ = Δt/(Δx)2 = (0.04)/(0.25)2 = 0.64
P = λ = 0.64
Q = (1-2λ) = -0.28
R = λ = 0.64

0.64 u_{i-1,j} - 0.28 u_{i,j} + 0.64 u_{i+1,j} + 0.08 = u_{i,j+1}

Se realizan 3 iteraciones:

i= 1, j=0

u_{1,1} = 0.64 u_{0,0} -0.28u_{1,0}+0.64 u_{2,0}+0.08 u_{1,1} = 0.64 [\sin(\pi*0)+0*(1-0)]- 0.28[\sin(\pi*0.25)+0.25*(1-0.25)] +0.64[\sin(\pi*0.5)+ 0.5*(1-0.5)]+0.08

u[1,1] =0.89

i = 2, j=0

0.64 u_{1,0} - 0.28 u_{2,0} + 0.64 u_{3,0} + 0.08 = u_{2,1}

u[1,0] = 1.25

i = 3, j=0

0.64 u_{2,0} - 0.28 u_{3,0} + 0.64 u_{4,0} + 0.08 = u_{3,1}

u[3,1] = 0.89

---

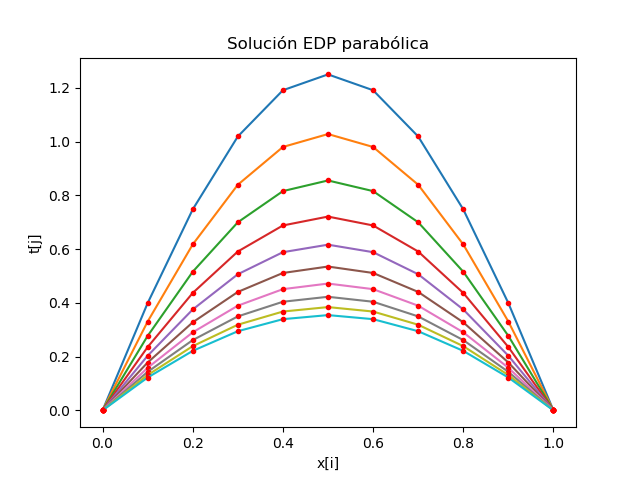
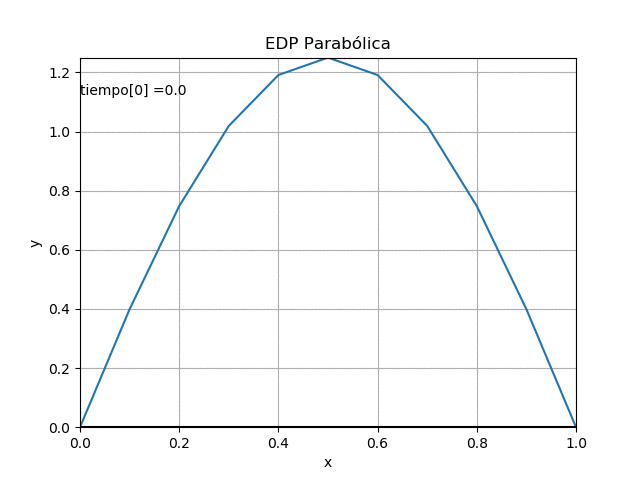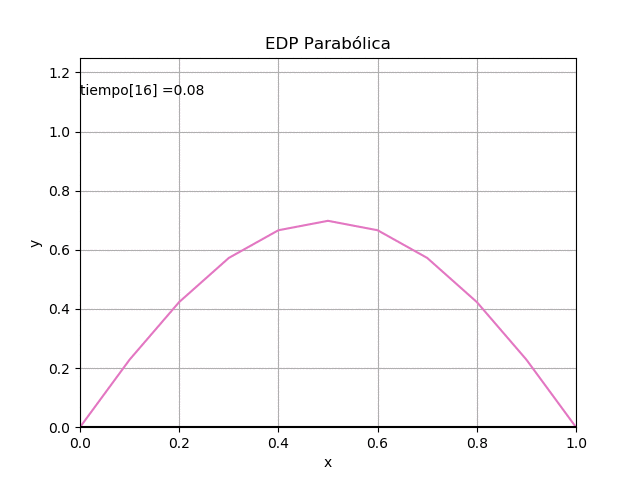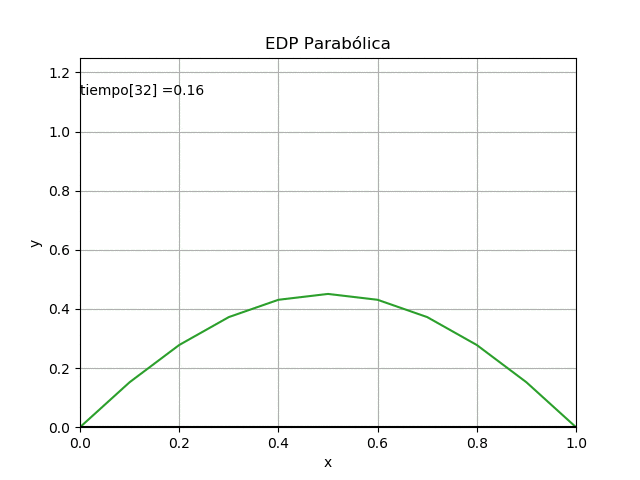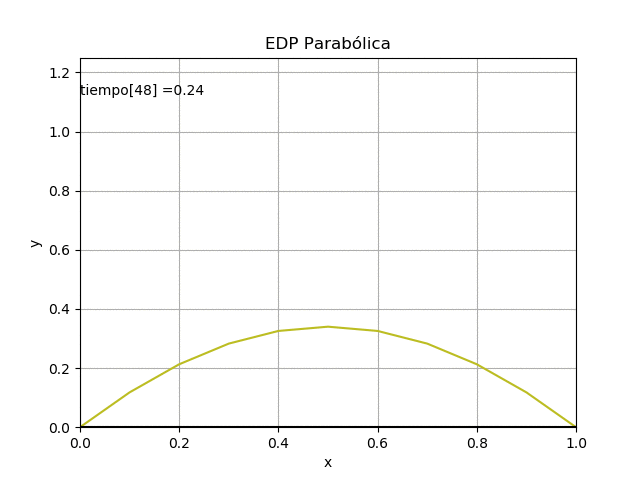
Algoritmo en Python

con los valores y ecuación del problema

# EDP parabólicas d2u/dx2  = K du/dt
# método explícito, usando diferencias finitas
# Referencia: Chapra 30.2 p.888 pdf.912
#       Rodriguez 10.2 p.406
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# Valores de frontera
Ta = 0
Tb = 0
T0 = lambda x: np.sin(np.pi*x)+x*(1-x)
# longitud en x
a = 0
b = 1
# Constante K
K = 1
# Tamaño de paso
dx = 0.1
dt = dx/10/2
# iteraciones en tiempo
n = 50

# PROCEDIMIENTO
# iteraciones en longitud
xi = np.arange(a,b+dx,dx)
m = len(xi)
ultimox = m-1

# Resultados en tabla u[x,t]
u = np.zeros(shape=(m,n), dtype=float)

# valores iniciales de u[:,j]
j=0
ultimot = n-1
u[0,j]= Ta
u[1:ultimox,j] = T0(xi[1:ultimox])
u[ultimox,j] = Tb

# factores P,Q,R
lamb = dt/(K*dx**2)
P = lamb
Q = 1 - 2*lamb
R = lamb

# Calcula U para cada tiempo + dt
j = 0
while not(j>=ultimot):
    u[0,j+1] = Ta
    for i in range(1,ultimox,1):
        u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j]+2*dt
    u[m-1,j+1] = Tb
    j=j+1

# SALIDA
print('Tabla de resultados')
np.set_printoptions(precision=2)
print(u)

# Gráfica
salto = int(n/10)
if (salto == 0):
    salto = 1
for j in range(0,n,salto):
    vector = u[:,j]
    plt.plot(xi,vector)
    plt.plot(xi,vector, '.r')
plt.xlabel('x[i]')
plt.ylabel('t[j]')
plt.title('Solución EDP parabólica')
plt.show()