Ejercicio: 3Eva_IIT2019_T2 Diferenciación, valor en frontera
La ecuación de problema de valor de frontera, con h = 1/4 = 0.25:
y'' = -(x+1)y' + 2y + (1-x^2) e^{-x}0 ≤ x ≤ 1
y(0) = -1
y(1) = 0
Se interpreta en la tabla como los valores que faltan por encontrar:
| i | 0 | 1 | 2 | 3 | 4 |
| xi | 0 | 1/4 | 1/2 | 3/4 | 1 |
| yi | -1 | 0 |
Por ejemplo, se usan las derivadas en diferencias finitas divididas centradas para segunda derivada y hacia adelante para primera derivada.
Semejante al procedimiento aplicado para métodos con EDO.
f''(x_i) = \frac{f(x_{i+1})-2f(x_{i})+f(x_{i-1})}{h^2} + O(h^2) f'(x_i) = \frac{f(x_{i+1})-f(x_i)}{h} + O(h)Se formula entonces la ecuación en forma discreta, usando solo los índices para los puntos yi:
\frac{y[i+1]-2y[i]+y[i-1]}{h^2} = -(x_i +1) \frac{y[i+1]-y[i]}{h} + 2y[i] + (1-x_i ^2) e^{-x_i}se multiplica todo por h2
y[i+1]-2y[i]+y[i-1] = -h(x_i +1)(y[i+1]-y[i]) + + 2 h^2 y[i] + h^2 (1-x_i ^2) e^{-x_i}y[i+1]-2y[i]+y[i-1] = -h(x_i +1)y[i+1] + + h(x_i +1)y[i] + 2 h^2 y[i] + h^2 (1-x_i ^2) e^{-x_i}
y[i+1](1 +h(x_i +1)) + y[i](-2 - h(x_i +1)-2 h^2)+y[i-1] = = h^2 (1-x_i ^2) e^{-x_i}
Ecuación que se aplica en cada uno de los puntos desconocidos con i =1,2,3
i = 1
y[2](1 +h(x_1 +1)) + y[1](-2 - h(x_1 +1)-2 h^2)+y[0] = = h^2 (1-x_1 ^2) e^{-x_1} y[2]\Big(1 +\frac{1}{4}\Big(\frac{1}{4} +1\Big)\Big) + y[1]\Big(-2 - \frac{1}{4}\Big(\frac{1}{4} +1\Big)-2 \Big(\frac{1}{4}\Big)^2\Big) -1 = = \Big(\frac{1}{4}\Big)^2 \Big(1-\Big(\frac{1}{4}\Big) ^2\Big) e^{-1/4} y[2]\Big(1 +\frac{5}{16} \Big) + y[1]\Big(-2 - \frac{5}{16}- \frac{2}{16}\Big) = = 1+ \frac{1}{16} \Big(1-\frac{1}{16}\Big) e^{-1/4} \frac{21}{16} y[2]- \frac{39}{16}y[1] = 1+ \frac{15}{16^2} e^{-1/4} - \frac{39}{16}y[1] + \frac{21}{16} y[2] = 1+ \frac{15}{16^2} e^{-1/4}multiplicando ambos lados de la ecuacion por 16 y reordenando
- 39 y[1] + 21 y[2] = 16+ \frac{15}{16} e^{-1/4}i = 2
y[3](1 +h(x_2 +1)) + y[2](-2 - h(x_2 +1)-2 h^2)+y[1] = = h^2 (1-x_2 ^2) e^{-x_2} y[3]\Big(1 +\frac{1}{4}\Big(\frac{1}{2} +1\Big)\Big) + y[2]\Big(-2 - \frac{1}{4}\Big(\frac{1}{2} +1\Big)-2 \Big(\frac{1}{4}\Big)^2\Big)+y[1] = = \Big(\frac{1}{4}\Big)^2 \Big(1-\Big(\frac{1}{2}\Big) ^2\Big) e^{-\frac{1}{2}} y[3]\Big(1 +\frac{3}{8}\Big) + y[2]\Big(-2 - \frac{1}{4}\Big(\frac{3}{2}\Big)- \frac{1}{8}\Big)+y[1] = = \Big(\frac{1}{16}\Big) \Big(1-\frac{1}{4}\Big) e^{-\frac{1}{2}} \frac{11}{8} y[3] - \frac{21}{8} y[2]+y[1] = \frac{1}{16} \Big(\frac{3}{4}\Big) e^{-\frac{1}{2}}multiplicando ambos lados por 8 y reordenando,
8y[1] - 21 y[2] + 11 y[3] = \frac{3}{8} e^{-\frac{1}{2}}i = 3
y[4](1 +h(x_3 +1)) + y[3](-2 - h(x_3 +1)-2 h^2)+y[2] = = h^2 (1-x_3 ^2) e^{-x_3} (0) \Big(1 +h\Big(x_3 +1\Big)\Big) + y[3]\Big(-2 - \frac{1}{4}\Big(\frac{3}{4} +1\Big)-2 \frac{1}{16}\Big)+y[2] = = \frac{1}{16}\Big (1-\Big(\frac{3}{4}\Big) ^2 \Big) e^{-3/4} y[3]\Big(-2 - \frac{7}{16} - \frac{2}{16}\Big)+y[2] = \frac{1}{16}\Big (1-\frac{9}{16}\Big) e^{-3/4}multiplicando todo por 16 y reordenando:
16 y[2] - 41 y[3] = \frac{7}{16} e^{-3/4}Con lo que se puede crear la forma matricial del sistema de ecuaciones Ax=B
\begin{bmatrix} -39 && 21 && 0\\8 && 21 && 11 \\ 0 && 16 && 41 \end{bmatrix}\begin{bmatrix} y[1]\\ y[2] \\y[3] \end{bmatrix} =\begin{bmatrix} 16+ \frac{15}{16} e^{-1/4} \\ \frac{3}{8} e^{-\frac{1}{2}} \\ \frac{7}{16} e^{-3/4} \end{bmatrix}con lo que resolviendo la matriz se obtienen los valroes para y[1], y[2], y[3]
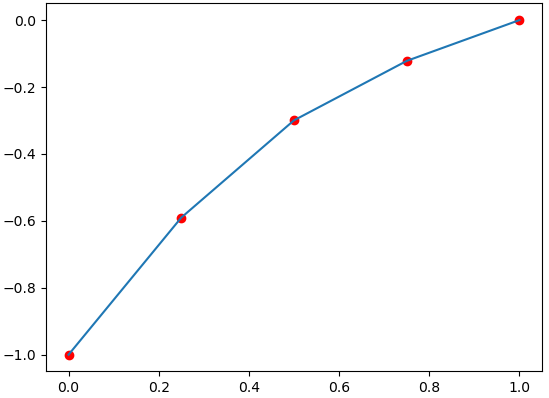
solución de matriz: [-0.59029143 -0.29958287 -0.12195088]
con lo que se completan los puntos de la tabla,
Solución de ecuación x[i] = [ 0. 0.25 0.5 0.75 1. ] y[i] = [-1. -0.59029143 -0.29958287 -0.12195088 0. ]
Algoritmo para solución de matriz con Python
tarea: modificar para cambiar el valor del tamaño de paso.
# Problema de Frontera import numpy as np import matplotlib.pyplot as plt # INGRESO h = 1/4 y0 = -1 y1 = 0 xi = np.arange(0,1+h,h) n = len(xi) yi = np.zeros(n,dtype=float) yi[0] = y0 yi[n-1] = y1 A = np.array([[-39.0, 21, 0], [ 8.0, -21, 11], [ 0.0, 16, -41]]) B = np.array([16+(15/16)*np.exp(-1/4), (3/8)*np.exp(-1/2), (7/16)*np.exp(-3/4)]) # PROCEDIMIENTO x = np.linalg.solve(A,B) for i in range(1,n-1,1): yi[i] = x[i-1] # SALIDA print('solución de matriz: ') print(x) print('Solución de ecuación') print('x[i] = ',xi) print('y[i] = ',yi) # Grafica plt.plot(xi,yi,'ro') plt.plot(xi,yi) plt.show()