Ejercicio: 3Eva_IT2019_T3 Difusión en sólidos
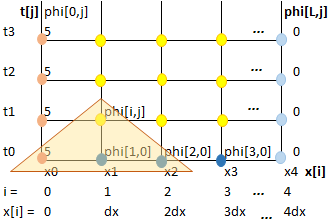
Siguiendo el procedimiento planteado en la sección EDP parabólicas, se plantea la malla del ejercicio:
Para plantear la ecuación en forma discreta:
\frac{\phi_{i,j+1}-\phi_{i,j}}{\Delta t}=D\frac{\phi_{i+1,j}-2\phi_{i,j}+\phi_{i-1,j}}{(\Delta x)^2}y resolver usando el método explícito para ecuaciones parabólicas, obteniendo el siguiente resultado:
\phi_{i,j+1}-\phi_{i,j}=D\frac{\Delta t }{\Delta x^2}(\phi_{i+1,j}-2\phi_{i,j}+\phi_{i-1,j}) \lambda = D\frac{\Delta t }{\Delta x^2} \phi_{i,j+1}-\phi_{i,j}=\lambda (\phi_{i+1,j}-2\phi_{i,j}+\phi_{i-1,j}) \phi_{i,j+1} =\lambda \phi_{i+1,j}-2\lambda\phi_{i,j}+\lambda\phi_{i-1,j}+\phi_{i,j} \phi_{i,j+1} =\lambda \phi_{i+1,j}(1-2\lambda)\phi_{i,j}+\lambda\phi_{i-1,j} \phi_{i,j+1} =P \phi_{i+1,j}+Q\phi_{i,j}+R\phi_{i-1,j}siendo:
P = λ = 0.16 (Δx/100)/Δx2 = 0.0016/Δx = 0.0016/0.02=0.08
Q = 1-2λ = 1-2*(0.08) = 0.84
R = λ =0.08
Iteración 1 en tiempo:
i=1, j=0
i=2,j=0
\phi_{2,1} =0.08 \phi_{3,0}+ 0.84\phi_{2,0}+0.08\phi_{1,0} = 0Para los proximos valores i>2, todos los resultados son 0
Iteración 2 en tiempo
i=1, j=1
\phi_{1,2} =0.08 (0)+ 0.84(0.4)+0.08(5)=0.736
i=2, j=1
i=3, j=1
\phi_{3,2} =0.08\phi_{4,1}+ 0.84\phi_{3,1}+0.08\phi_{2,1}=0Para los proximos valores i>3, todos los resultados son 0
Tarea: Desarrollar la iteración 3 en el tiempo.
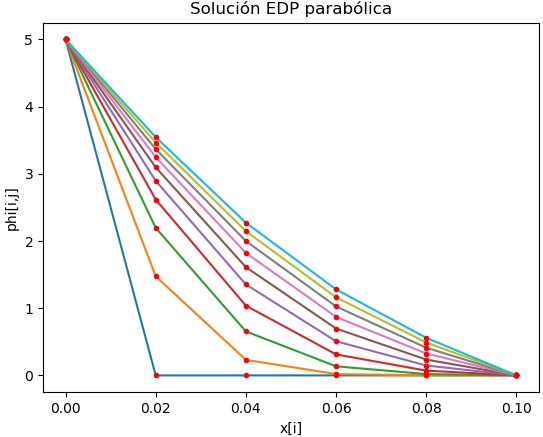
siguiendo las iteraciones se tiene la siguiente tabla:
[[5.0, 0.000, 0.000, 0.00000, 0.00000 , 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [5.0, 0.400, 0.000, 0.00000, 0.00000 , 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [5.0, 0.736, 0.032, 0.00000, 0.00000 , 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [5.0, 1.021, 0.085, 0.00256, 0.00000 , 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], [5.0, 1.264, 0.153, 0.00901, 0.00020, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0] ... ]
Con lo que se obtiene la siguiente gráfica.
El resultado se interpreta mejor con una animación: (tarea)
Tarea: Presentar el orden de error de la ecuación basado en las fórmulas de diferenciación
Algorirmo en Python
# 3Eva_IT2019_T3 Difusión en sólidos # EDP parabólicas. método explícito,usando diferencias finitas import numpy as np import matplotlib.pyplot as plt # INGRESO # Valores de frontera Ta = 5 Tb = 0 T0 = 0 # longitud en x a = 0 b = 0.1 # Constante K K = 1/(1.6e-1) # Tamaño de paso dx = 0.02 dt = dx/100 # iteraciones en tiempo n = 50 # PROCEDIMIENTO # iteraciones en longitud xi = np.arange(a,b+dx,dx) m = len(xi) ultimox = m-1 # Resultados en tabla u[x,t] u = np.zeros(shape=(m,n), dtype=float) # valores iniciales de u[:,j] j=0 ultimot = n-1 u[0,j]= Ta u[1:ultimox,j] = T0 u[ultimox,j] = Tb # factores P,Q,R lamb = dt/(K*dx**2) P = lamb Q = 1 - 2*lamb R = lamb # Calcula U para cada tiempo + dt j = 0 while not(j>=ultimot): u[0,j+1] = Ta for i in range(1,ultimox,1): u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j] u[m-1,j+1] = Tb j=j+1 # SALIDA print('Tabla de resultados') np.set_printoptions(precision=2) print(u) # Gráfica salto = int(n/10) if (salto == 0): salto = 1 for j in range(0,n,salto): vector = u[:,j] plt.plot(xi,vector) plt.plot(xi,vector, '.r') plt.xlabel('x[i]') plt.ylabel('phi[i,j]') plt.title('Solución EDP parabólica') plt.show()
La animación se complementa con lo mostrado en la sección de Unidades.