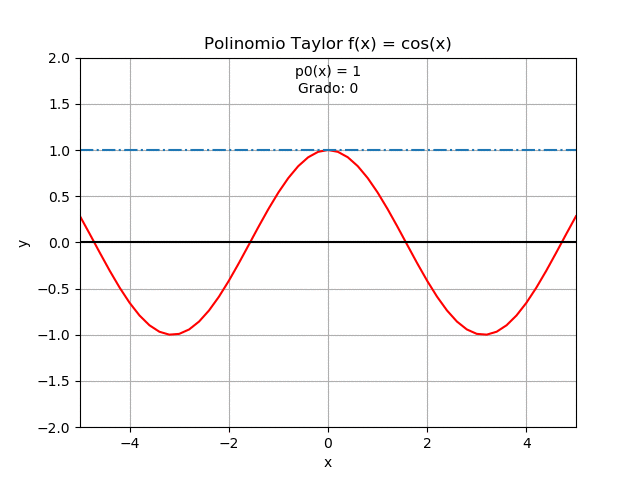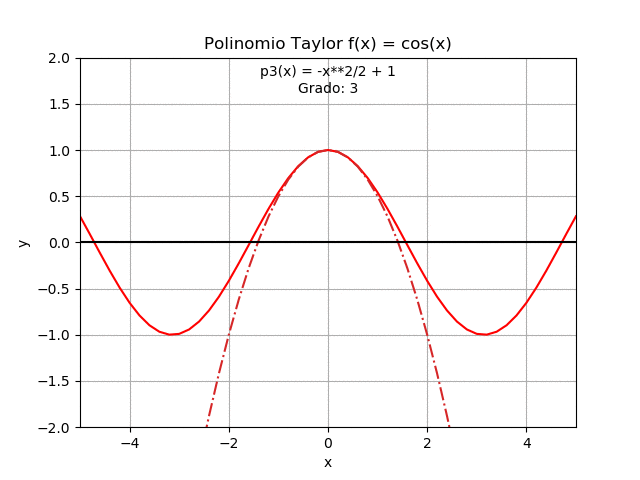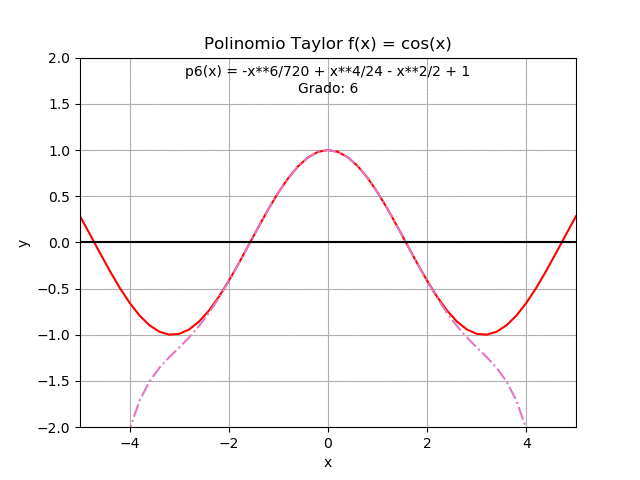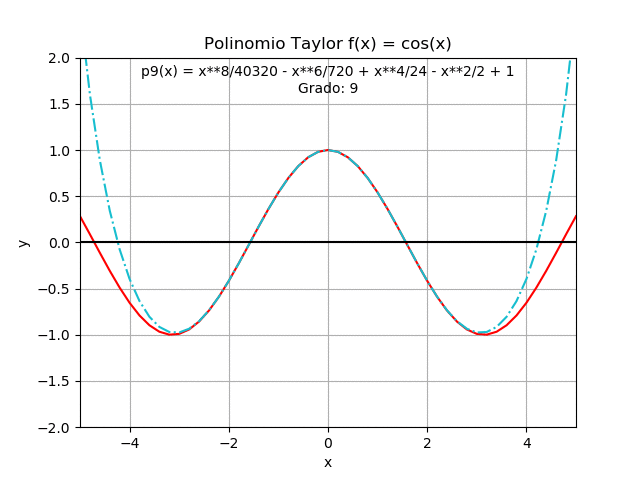
Referencia: Burden 7Ed, Cap 1.1 Ejemplo 3. p11, 10Ed p8. Chapra, 4.1 p80, Taylor Series (Wikipedia)
El ejercicio se presenta como un complemento para la sección 1.4 que permite obtener una gráfica animada.
Esta sección es complementaria y usada solo como referencia para exponer el tema. Normalmente se da una explicación breve en el laboratorio de computadoras.
la parte adicional se muestra a partir de:
# SALIDA # GRAFICA CON ANIMACION ------------
Algoritmo completo en Python
El tema en detalle se desarrolla en Movimiento circular – Una partícula, animación con matplotlib-Python del curso de Fundamentos de Programación
El algoritmo requiere disponer de la librería"pillow".
# Aproximación Polinomio de Taylor alrededor de x0 # f(x) en forma simbólica con sympy import numpy as np import math import sympy as sym def politaylor(fx,x0,n): k = 0 polinomio = 0 while (k <= n): derivada = fx.diff(x,k) derivadax0 = derivada.subs(x,x0) divisor = math.factorial(k) terminok = (derivadax0/divisor)*(x-x0)**k polinomio = polinomio + terminok k = k + 1 return(polinomio) # PROGRAMA ------------- # Capitulo 1 Ejemplo 2, Burden p11, pdf 21 # INGRESO x = sym.Symbol('x') fx = sym.cos(x) x0 = 0 n = 10 # Grado polinomio Taylor a = -5 # intervalo [a,b] b = 5 muestras = 51 # PROCEDIMIENTO # tabla polinomios px_tabla = [] for grado in range(0,n,1): polinomio = politaylor(fx,x0,grado) px_tabla.append(polinomio) # SALIDA print('grado : polinomio') for grado in range(0,n,1): px = px_tabla[grado] print(str(grado)+ ' : '+str(px)) # print('polinomio: ') # sym.pprint(px) # print() # GRAFICA - TABLA polinomios ------ xi = np.linspace(a,b,muestras) # Forma lambda, simplifica evaluación fxn = sym.utilities.lambdify(x,fx,'numpy') fi = fxn(xi) # lineas de cada grado de polinomio px_lineas = np.zeros(shape=(n,muestras), dtype =float) for grado in range(0,n,1): polinomio = px_tabla[grado] px = sym.utilities.lambdify(x,polinomio,'numpy') px_lineas[grado] = px(xi) # SALIDA # GRAFICA CON ANIMACION ------------ import matplotlib.pyplot as plt import matplotlib.animation as animation # Parametros de trama/foto narchivo = 'Taylor01' # nombre archivo retardo = 700 # milisegundos entre tramas tramas = len(px_lineas) ymax = 2*np.max(np.abs(fi)) # GRAFICA figura figura, ejes = plt.subplots() # Función Base fx_linea, = ejes.plot(xi,fi,'r') # Polinomios de tablapoli grado = 0 px_unalinea, = ejes.plot(xi, px_lineas[0], '-.', label='grado: 0') # Configura gráfica plt.xlim([a,b]) plt.ylim([-ymax,ymax]) plt.axhline(0, color='k') # horizontal en cero plt.title('Polinomio Taylor: '+'f(x) = ' + str(fx)) plt.xlabel('x') plt.ylabel('y') plt.grid() # cuadros de texto en gráfico txt_x = (b+a)/2 txt_y = ymax*(1-0.1) texto_poli = ejes.text(txt_x, txt_y*(1), 'p(x):', horizontalalignment='center') texto_grado = ejes.text(txt_x, txt_y*(1-0.1), 'grado:', horizontalalignment='center') # Nueva Trama def unatrama(i,xi,pxi): # actualiza cada linea px_unalinea.set_xdata(xi) px_unalinea.set_ydata(pxi[i]) etiquetap = 'p'+str(i)+'(x) = '+str(px_tabla[i]) px_unalinea.set_label(etiquetap) # actualiza texto texto_poli.set_text(etiquetap) texto_grado.set_text('Grado: '+str(i)) # color de la línea if (i<=9): lineacolor = 'C'+str(i) else: numerocolor = i%10 lineacolor = 'C'+str(numerocolor) px_unalinea.set_color(lineacolor) return (px_unalinea, texto_poli, texto_grado) # Limpia Trama anterior def limpiatrama(): px_unalinea.set_ydata(np.ma.array(xi, mask=True)) px_unalinea.set_label('') texto_poli.set_text('') texto_grado.set_text('') return (px_unalinea,texto_poli, texto_grado) # Trama contador i = np.arange(0,tramas,1) ani = animation.FuncAnimation(figura, unatrama, i , fargs = (xi,px_lineas), init_func = limpiatrama, interval = retardo, blit=True) # Graba Archivo GIFAnimado y video ani.save(narchivo+'_GIFanimado.gif',writer='pillow') # ani.save(narchivo+'_video.mp4') plt.draw() plt.show()