[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
…
Ejemplo 1 – Secuencia de Fibonacci
Referencia: Ejercicio 12 de 3.3.3 Tarea-Lazos
La secuencia de Fibonacci es muy reconocida en la matemática. Como introducción al tema se recomienda observar el video de «misterio de las matemáticas» que tiene una explicación interesante entre los tiempos 2:33 y 6:40, por lo que el video inicia en el minuto 2:33.
La secuencia se desarrolla a partir de dos números: 1 y 1
El siguiente término se obtiene sumando los dos anteriores:
1 1 2 3 5 8 13 21 ...
a+b=c
a+b=c
a+b=c
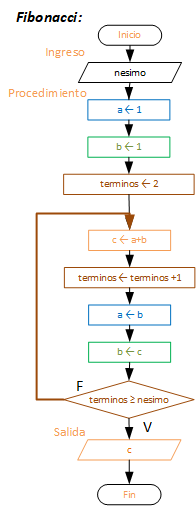
El algoritmo primero se presenta en el diagrama de flujo para facilidad visual de los pasos.
Al requerir mostrar toda la secuencia, en lugar de un solo valor, aparece la necesidad de usar un vector.
Para éste caso usamos la librería numpy para obtener los siguientes resultados:
¿cuál término?: 8 término n-ésimo: 21 secuencia: [ 1 1 2 3 5 8 13 21] >>>
Algoritmo en Python
Se modifican las instrucciones para añadir la secuencia en un vector:
# secuencia de fibonacci # usando vectores import numpy as np # INGRESO nesimo = int(input('¿cuál término?: ')) # PROCEDIMIENTO a = 1 b = 1 terminos = 2 secuencia = np.zeros(nesimo,dtype = int) secuencia[0] = 1 secuencia[1] = 1 while not(terminos>=nesimo): c = a+b secuencia[terminos] = c terminos = terminos+1 a = b b = c # SALIDA print('término n-ésimo: ',c) print('secuencia: ', secuencia)
Ejemplo 2: 1Eva_IIT2015_T3 Vector de números primos
Primero desarrolle el algoritmo para un número cualquiera «n«. 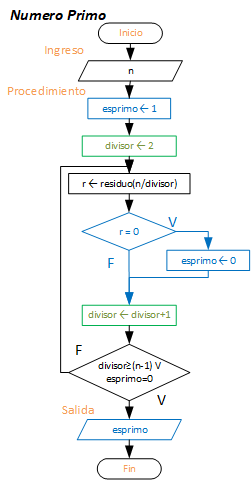
Como hipótesis, inicie considerando que el número es primo, esprimo=1, luego pruebe con cada uno de los divisores en el intervalo entre 2 y (n-1).
La divisibilidad se revisa con el residuo entre el número n y los divisiores del intervalo [2,n-1].
Primero con divisor=2. El número 1 no cuenta pues todos los números son divisibles para 1.
Si el residuo calculado tuvo resultado cero, el número n no es primo, esprimo=0. Continua las pruebas con el siguiente divisor, divisor = divisor +1
Se revisa si se han probado con todos los números inferiores a n o que el resultado ya no es primo, esprimo=0.
Se muestran los resultados.
El esquema del ejemplo se muestra en el diagrama de flujo.
Algoritmo en Python
Convirtiendo las instrucciones de diagrama de flujo a instrucciones en Python:
# 1ra Evaluación II Término 2015. Tema 3 # numeros primos # INGRESO n = int(input('primo a revisar: ')) # PROCEDIMIENTO ES PRIMO esprimo = 1 divisor = 2 while not(divisor>=(n-1) or esprimo==0): residuo = n%divisor if (residuo==0): esprimo=0 divisor = divisor+1 # SALIDA print('numero primo: ', esprimo)
Tarea
En una secuencia de números enteros, identifique cuales son números primos.
Reutilice el algoritmo anterior para almacenar cada resultado en un vector, indicando 1 si es primo y 0 si no lo es.
Luego de probar que el algoritmo funciona, realice un bloque de ingreso para la secuencia de prueba.
numeros prueba: [ 2 3 4 5 6 7 8 9 10] cumple esprimo: [ 1 1 0 1 0 1 0 0 0] >>>
# 1ra Evaluación II Término 2015 # numeros primos import numpy as np # INGRESO probar = np.array([2,3,4,5,6,7,8,9,10]) # PROCEDIMIENTO tamano = len(probar) cumple = np.ones(tamano, dtype=int) posicion = 0 while not(posicion==tamano): n = probar[posicion] # PROCEDIMIENTO ES PRIMO esprimo = 1 i = 2 while not(i>=(n-1) or esprimo==0): r = n%i if (r==0): esprimo=0 i = i+1 cumple[posicion] = esprimo posicion = posicion+1 # SALIDA print('numeros prueba: ', probar) print('cumple esprimo: ', cumple)
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
…
Ejercicios resueltos de vectores como arreglos en Python
Vectores – Arreglos unidimensionales con Python y Numpy
1Eva_IT2013_T4 Tabular atención al cliente
solución propuesta: s1Eva_IT2013_T4 Tabular atención al cliente
1Eva_IIT2002_T2 Color de placas de vehículos
solución propuesta: s1Eva_IIT2002_T2 Color de placas de vehículos
1Eva_IT2008_T2 Criba de Eratóstenes
solución propuesta: s1Eva_IT2008_T2 Criba de Eratóstenes
1Eva_IT2002_T3 Calificaciones mejores que alguien
Arreglos unidimensionales y números aleatorios
1Eva_IT2008_T3 Simular precio de petroleo
Solución literal c: s1Eva_IT2008_T3 Simular precio de petroleo
1Eva_IIT2010_T3 Juego del amigo secreto
Solución propuesta: s1Eva_IIT2010_T3 Juego del amigo secreto
1Eva_IIT2007_T2 Juego de la Ruleta
Solución propuesta: s1Eva_IIT2007_T2 Juego de la Ruleta
Arreglos, acumuladores y contadores
1Eva_IIT2010_T1 Censo de instrucción por género
Solución propuesta: s1Eva_IIT2010_T1 Censo de instrucción por género
1Eva_IT2011_T3 Calcular ventas por región
Solución propuesta: s1Eva_IT2011_T3 Calcular ventas por región
Solución propuesta: s1Eva_IT2013_T1 Primos gemelos
1Eva_IT2008_T2 Criba de Eratóstenes
Solución propuesta: s1Eva_IT2008_T2 Criba de Eratóstenes
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
Ejercicios para resolver sobre de arreglos en programación
1Eva_IT2005_T3 Arreglo aleatorio binario a decimal
1Eva_IT2001_T6 Piloto y copiloto para nave
1Eva_IIT2002_T3 Conjetura de Ullman
1Eva_IIT2008_T4 Área del polígono convexo por triángulos
[ Ejemplos ] [ Ejercicios resueltos ] [ ejercicios para resolver ]
