Ejercicio: 1Eva_IT2008_T2 Criba de Eratóstenes
Propuesta de solución en Python: py_pdf, también en versión matlab: m_pdf
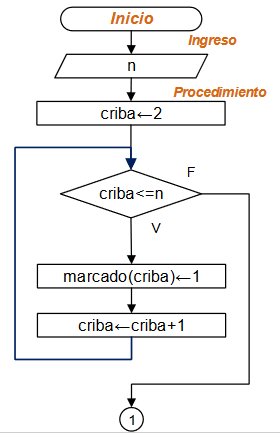
Llenar un arreglo de marcas o tachado con la hipótesis que todos son primos(1).
# PROCEDIMIENTO marcado = np.zeros((n+1),dtype=int) # hipotesis: todos son primos criba = 2 while (criba<=n): marcado[criba] = 1 criba = criba+1
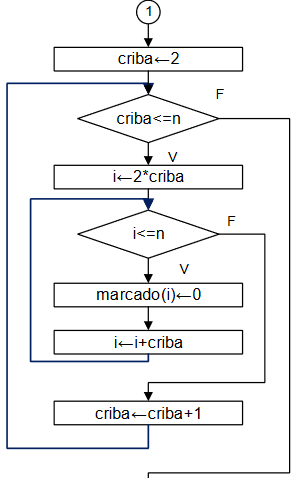
La prueba de hipótesis consiste en usar un indicador para el número de criba, y otro indicador i para anular marcando con cero (0) las posiciones de los múltiplos.
Inicie eliminando los múltiplos de 2, para luego cambiar a los múltiplos de 3, etc.
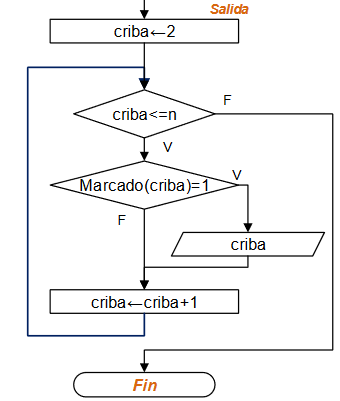
Mostrar como resultado solo aquellos números mantienen en marcas válidas (1).
Tarea: Analizar si es necesario hacer funcionar el algoritmo de la prueba de hipótesis hasta n o un número menor. Realizar la validación que n sea mayor que 1.
# ICM00794-Fundamentos de Computación - FCNM-ESPOL # 1Eva_IT2008_T2 Criba de Eratóstenes # Propuesta: edelros@espol.edu.ec import numpy as np # INGRESO n = int(input('primos menores que: ')) # PROCEDIMIENTO marcado = np.zeros((n+1),dtype=int) # hipotesis: todos son primos criba = 2 while (criba<=n): marcado[criba] = 1 criba = criba+1 # no son primos los múltiplos criba = 2 while (criba<=n): # revisa el primer múltiplo i = criba * 2 while (i<=n): marcado[i] = 0 i = i + criba criba = criba+1 # SALIDA criba = 2 while (criba<=n): if marcado[criba]==1: print(criba) criba = criba+1
resultado del algoritmo
primos menores que: 30 2 3 5 7 11 13 17 19 23 29 >>>
Otra forma de plantear el algoritmo
# 1ra Evaluación I Término 2008 # Tema 2. Criba de Eratóstenes import numpy as np # INGRESO n = int(input('cuantos numeros analiza: ')) # PROCEDIMIENTO # vector de números naturales natural = np.zeros(n, dtype=int) posicion = 0 while not(posicion>=n): natural[posicion] = posicion posicion = posicion +1 # hipotesis todos cumplen cumple = np.ones(n,dtype = int) # Tarea: analiza cada posición posicion = 2 # elimina multiplos / no cumplen contador = 2 tacha = posicion *contador while not(tacha>(n-1)): tacha = posicion *contador if tacha<(n-1): cumple[tacha] = 0 contador = contador +1 # SALIDA # solo valores de la posicion 2 en adelante print(natural[2:]) print(cumple[2:])
mostrando el siguiente resultado:
cuantos numeros analiza: 50 [ 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49] [1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1] >>>