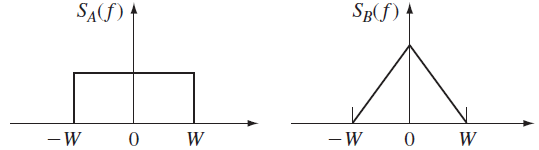
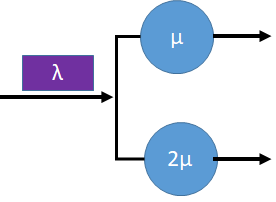
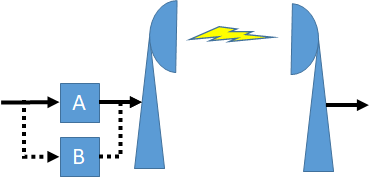
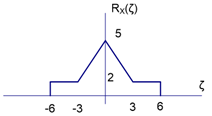
3ra Evaluación I Término 2017-2018. Septiembre 12, 2017
Tema 1 (30 puntos). En una ciudad existen 3 cadenas de supermercados (X, Y, Z) y se dispone de la movilidad de los clientes entre ellos. 
En septiembre de un total de 1 millón de clientes, la cuarta parte realiza las compras en el supermercado X, 1/3 va al supermercado Y, mientras que 5/12 adquiere productos en el supermercado Z.
En cada mes el supermercado X retiene el 90% de sus clientes y pierde el 10% que van al supermercado Y.
Se determinó que del supermercado Y solo retiene el 5% de sus clientes y el 85% se cambian a X y el resto va a Z.
El supermercado Z retiene solo el 40% de su clientela, el 50% va al supermercado X y el 10 % se cambia a Y.
a) Determine los estados del problema
b) Realice el diagrama de transición
c) Elabore la matriz de transición correspondiente
d) Clasifique los estados del problema
e) Determine el vector de probabilidad estable
f) ¿Cuál es la proporción de clientes para los supermercados al mes siguiente?
g) Suponga que observa un cliente del supermercado Y:
1. Determine la probabilidad que en el siguiente periodo sea cliente de Z.
2. Luego el cliente del numeral anterior al segundo periodo decida cambiarse a X
3. Para un cliente de Y, determine la probabilidad que luego de tres periodos no termine comprando en X.
Rúbrica: Literales a al f (4 puntos cada uno), literal g (6 puntos).