Categoría: Densidad Espectral Potencia

Referencia: Problema León García 10.10 p.636

Sean X(t) y Y(t) procesos independientes estacionarios en el sentido amplio.

Defina Z(t) = X(t) Y(t)

a) Muestre que Z(t) es estacionario en el sentido amplio (WSS).

b) Encuentre R_Z(τ) y S_Z(f)

Solución propuesta:

E[Z(t)] = E[X(t) Y(t)]

que por ser independientes,

= E[ X(t) ] E[ Y(t) ] = m_X m_Y

R_Z(τ) = E[ Z(t) Z(t+τ) ]
= E[ X(t)Y(t) X(t+τ)Y(t+τ) ]
= E[ X(t)X(t+τ) Y(t)Y(t+τ) ]
= E[ X(t)X(t+τ)] E[ Y(t)Y(t+τ) ]
= R_X(τ) R_Y(τ)

que tambien dependen solo de τ, por lo que Z(t) es WSS

S_Z(f) = F[R_Z(τ)]
= F[R_X(τ) R_Y(τ)]
= S_X(f) * S_Y(f) (convolución)

Referencia: Problema León García 10.6 p.636

Sea Z(t) = X(t) + Y(t)

¿Bajo qué condiciones S_Z(f) = S_X(f) + S_Y(f)?

Solución Propuesta:

E[ Z(t)Z(t+τ) ] = E[ [X(t) + Y(t)][X(t+τ) + Y(t+τ)] ]

= E[ X(t)X(t+τ) + Y(t) X(t+τ) + X(t)Y(t+τ) + Y(t)Y(t+τ) ]

= E[  X(t)X(t+τ) ] +E[ Y(t) X(t+τ) ] + E[ X(t)Y(t+τ) ] + E[ Y(t)Y(t+τ) ]

R_Z(τ) = R_X(τ) + R_YX(τ)  + R_XY(τ)  + R_Y(τ)

S_Z(f) = S_X(f) + S_YX(f)  + S_XY(f)  + S_Y(f)

Si X(t) y Y(t) son ortogonales, entonces:

R_XY(τ)  = R_YX(τ) = 0

S_Z(f) = S_X(f) + 0  + 0  + S_Y(f)

S_Z(f) = S_X(f) +  S_Y(f)

 

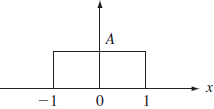
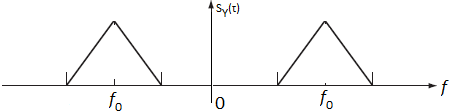Referencia: Problema León García 10.4 p.635

a) Encuentre la función de autocorrelación correspondiente a la densidad espectral de potencia de la figura.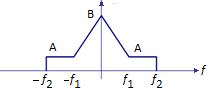

b) Encuentre el total de la potencia promedio

c) Grafique la potencia en el rango de |f| > f₀ como función de f₀>0.

Solución propuesta:

a)
$S_X(f) = A \prod \Big(\frac{f}{2f_2} \Big) + (B-A) \bigwedge \Big( \frac{f}{f_1} \Big)$

$R_X(\tau) = F^{-1}\Big[ A \prod \Big(\frac{f}{2f_2} \Big) \Big] + F^{-1} \Big[ (B-A) \bigwedge \Big( \frac{f}{f_1} \Big) \Big]$ $= 2A f_2 [Sa (2\pi f_2 \tau)] + (B-A) f_1 [Sa (\pi f_1 \tau) ]^2$

b)
$P = \int_{-\infty}^{\infty} S_X(f) \delta f$

$= A(2f_2) + (2f_1)\frac{(B-A)}{2}$ $= 2A f_2 + (B-A)f_1$

c)

la potencia en función de la frecuencia es par, por lo que se integra entre 0 y f₀ y se duplica para el rango entre [-f₀, f₀]
$2\int_{0}^{f_0} S_X(f) \delta f =$

primera sección: 0 < f₀ < f₁

$2\int_{0}^{f_0} \Big[ \Big( -\frac{B-A}{f_1} \Big)f +B\Big] \delta f$ $= 2 \Big[ \Big(-\frac{B-A}{f_1}\Big) \frac{ f^2}{2} +Bf \Big] \Big|_{0}^{f_0}$ $= \Big(-\frac{B-A}{f_1}\Big) f_0^2 +2Bf_0$ $= 2Bf_0 -\frac{B-A}{f_1} f_0^2$

segunda sección: f₁ < f₀ < f₂
$= 2[ \frac{B-A}{2}f_1 + A(f_0 - f_1) \Big]$

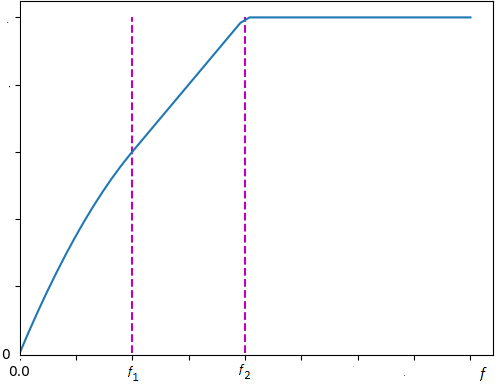
# leon- garcia 10.4
# literal c
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
A = 1
B = 2
f1 = 1
f2 = 2

n = 50
final = 4
# PROCEDIMIENTO
f = np.linspace(0,final,n)
P = np.zeros(n,dtype=float)
for i in range(0,n,1):
    if f[i]= f1 and f[i]f2:
        P[i] = 2*(((B+A)/2)*f1 + A*(f2-f1))

# SALIDA Grafica
plt.plot(f,P)
plt.vlines(f1,0,2.5*B, color='m', linestyle='dashed')
plt.vlines(f2,0,2.5*B, color='m', linestyle='dashed')
plt.show()

Referencia: Problema León García 10.3 p.635

a) Encuentre la densidad espectral de potencia S_Y(f) de un proceso aleatorio con función de autocorrelación R_X(τ) cos(2π f₀ τ), donde R_X(τ) es también una función de autocorrelación.

b) Grafique S_Y(f) si R_X(τ) como en el problema 10.1a.

Solución propuesta:

$R_Y(\tau) = R_X(\tau) \cos(2\pi f_0 \tau)$ $S_Y(f) = F\Big[ R_X(\tau) \cos(2\pi f_0 \tau) \Big]$ $= F\Big[ R_X(\tau) \frac {e^{j2\pi f_0 \tau} + e^{-j2\pi f_0 \tau}}{2} \Big]$ $= \frac{1}{2} F\Big[ R_X(\tau) e^{j2\pi f_0 \tau} \Big] + \frac{1}{2} F\Big[ R_X(\tau) e^{-j2\pi f_0 \tau} \Big]$ $= \frac{1}{2} S_X(f-f_0) + \frac{1}{2} S_X(f+f_0)$

donde S_X (f) = F[R_X(τ)]

Referencia: Problema León García 10.2 p.635

Sea p(x) una función rectangular. ¿ R_X(τ) = p(τ/T) es una función de autocorrelación?

Solución propuesta:

T=2, es función rectangular es el ancho de la base.

$S_Y(f) = F\Big[ \prod \Big(\frac{\tau}{T} \Big) \Big]$ $= 2AT \frac {Sen(2\pi f \tau)}{2\pi fT}$ $= AT Sa (\pi f\tau)$

La función S_X(f) es negativa para algunos rangos de f. Dado que la densidad espectral de potencia es no negativa, la función rectangilar en el tiempo no es una función de autocorrelacón válida.

 

Referencia: Problema León García 10.1 p.635

Sea g(x) una función triangular.

amplitud = A
T = 1 , en triangulares T es la mitad de la base del triángulo.

a) Encuentre la densidad espectral de potencia correspondiente a R_X(τ) = g(τ/T)

b) Encuentre la autocorrelación correspondiente a la densidad espectral de potencia S_X(f) = g(f/W)

Solución propuesta:
a)
$S_x(f) = F\Big[ g \Big(\frac{\tau}{T} \Big) \Big]$

$= AT \Big(\frac{sin\frac{\omega T}{2}}{\frac{\omega T}{2}} \Big)^2$ $= AT \big[Sa(\pi f T) \big]^2$

b)

$S_x(f) = F\Big[ g \Big(\frac{f}{W} \Big) \Big]$ $R_X (\tau) = AW \Big(\frac{sin\frac{W \tau}{2}}{\frac{W \tau}{2}} \Big)^2$ $= AW \big[Sa(\pi f \tau) \big]^2$