Referencia: Leon-García p.99, Gubner p.67
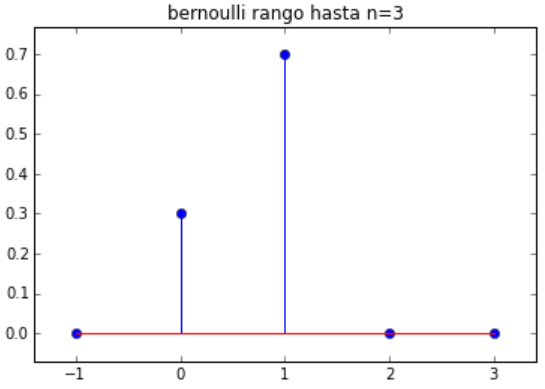
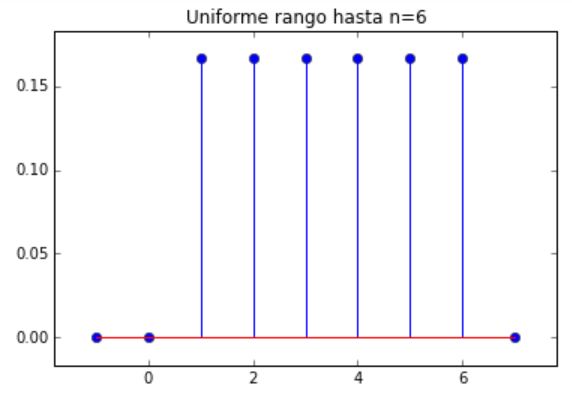
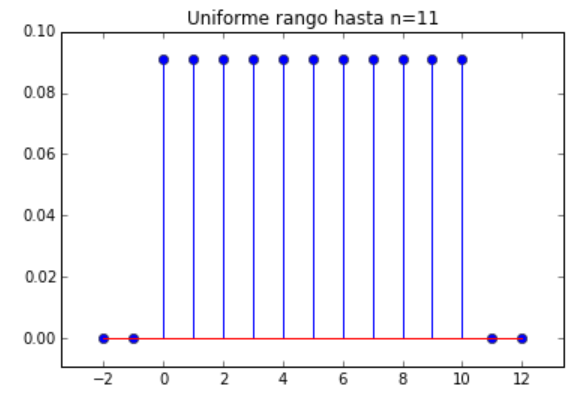
Variables Aleatorias discretas – Distribución de Probabilidad PMF
Una variable aleatoria discreta X se define como una variable que toma valores de un espacio muestral
Sx = {x1, x2, x3, …}.
Una variable aleatoria discreta finita tiene un espacio muestral finito, es decir:
Sx = {x1, x2, x3, …, xn}.
Si el interes es encontrar las probabilidades de un evento
Ak = {w: X(w) = xk}
La Distribución de probabilidad (Probability mass function pmf) de una variable aleatoria discreta X se define como:
px = P[X = x] = P{w: X(w) = x} para un x real
La distribución de probabilidad (pmf) de px(x) satisface las tres propiedades que se requieren para calcular las probabilidades de los eventos de una variable discreta X:
1. p_x(x) \geq 0 \text{, para todo x}
2. \sum \limits_{x\in S_x}p_x(x) = \sum \limits_{k}p_x(x_k) = \sum \limits_{k}P(A_k) = 1
3. P[X \in B] = \sum \limits_{x\in B} p_x(x) \text{, donde } B \subset S_x
Ejemplo
Gubner 2.5 número de caras en tres lanzamientos de una moneda
Encuentre la distribución de probabilidad (pmf) de X, suponiendo que los lados de la moneda son igualmente probables.
Solución: Del ejemplo desarrollado antes, se obtuvo que:
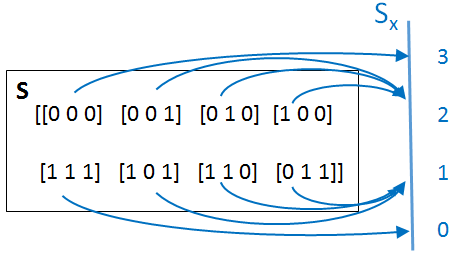
Sx: [0 1 2 3]
evento, X(evento)
[0 0 0] 3
[0 0 1] 2
[0 1 0] 2
[0 1 1] 1
[1 0 0] 2
[1 0 1] 1
[1 1 0] 1
[1 1 1] 0
Para calcular px(0) = P(X=0), e indentificando los resultados w que pertenecen al evento {w:X(w)=0} ={111}.
Entonces :
px(0) = P(X=0) = P({111}) = |{111}|/|S| = 1/8
siguiendo el mismo procedimiento:
px(1) = P(X=1) = P({011, 101, 110}) = 3/8
px(2) = P(X=2) = P({001,010,001}) = 3/8
px(3) = P(X=3) = P({000}) = 1/8
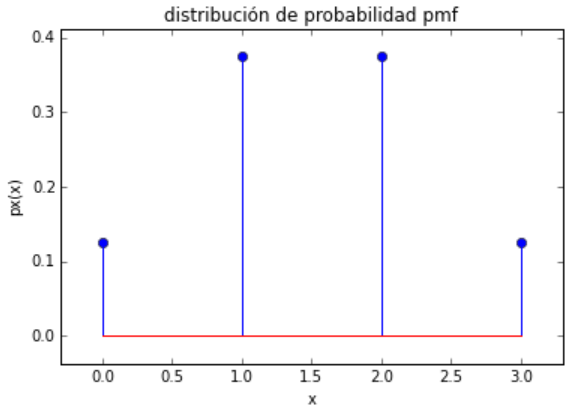
lo que permite graficar la distribución de probabilidad
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
# del ejercicio de tres lanzamientos de moneda
X = [3,2,2,1,2,1,1,0]
# PROCEDIMIENTO
[unicos, cuenta] = np.unique(X, return_counts=True)
frelativa = cuenta/len(X)
# SALIDA
print('x: ', unicos)
print('px: ', frelativa)
# grafica
plt.stem(unicos,frelativa)
plt.title('distribución de probabilidad pmf')
plt.xlabel('x')
plt.ylabel('px(x)')
plt.margins(0.1)
plt.show()
x: [0 1 2 3]
px: [ 0.125 0.375 0.375 0.125]
suponga ahora que la probabilidad de salida de una cara es p, y que la cara contraria es (1-p), con lo que se procederia como:
px(0) = P(X=0) = P({111}) = (1-p)3
px(1) = P(X=1) = P({011, 101, 110}) = 3(1-p)2p
px(2) = P(X=2) = P({001,010,001}) = 3(1-p)p2
px(3) = P(X=3) = P({000}) = p3
Distribución de probabilidad del juego de apuestas
León-García E3.6 p.101
Un jugador recibe $1 si el número de caras en tres lanzamientos de una moneda es 2, $8 si el número de caras es 3, pero nada en otro caso. Encuentre la pmf de lo que gana Y.
siguiendo con el ejemplo anterior
dinero = np.arange(8+1)
pgana = np.zeros(len(dinero),dtype=float)
pgana[8] = frelativa[3]
pgana[1] = frelativa[2]
pgana[0] = np.sum(frelativa[0:2])
# SALIDA
print('Y: ', dinero)
print('py: ', pgana)
# grafica
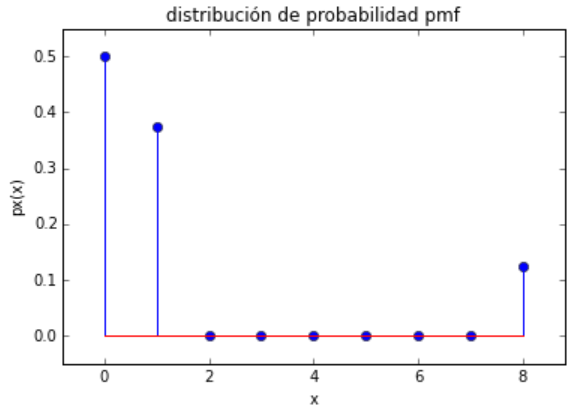
plt.stem(dinero,pgana)
plt.title('distribución de probabilidad pmf')
plt.xlabel('x')
plt.ylabel('px(x)')
plt.margins(0.1)
plt.show()
Y: [ 0 1 2 3 4 5 6 7 8 ]
py: [ 0.5 0.375 0. 0. 0. 0. 0. 0. 0.125]