Categoría: Procesos Aleatorios – Introducción

Ejemplo: Caminata de pasos aleatorios o Random Step Process

Referencia: Leon-García. E9.14 p.500

Un contador «up-down» o «sube-baja» genera pulsos +1 ó -1. La entrada del contador está dada por D_n = 2 I_n-1, donde I_n es un proceso aleatorio tipo Bernoulli.

$D_n = \begin{cases} +1 & \quad \text{, } I_n = 1\\ -1 & \quad \text{, } I_n = 0 \end{cases}$

Por ejemplo D_n representaría el cambio en la posición de una partícula que se mueve a lo largo de una linea recta, y cambia entre ±1 cada unidad de tiempo. Ej: n=20, p=0.5

La media de D_n es:

mD(n) = E[Dn] 
    = E[ 2In -1] = 2E[In]-1
    = 2p - 1

La varianza de D_n se encuentra como:

VAR[Dn] = VAR[2In - 1]
    = 22 VAR[In]
    = 4p(1 - p)

Las probabilidades de los eventos de D_n se calculan como en el ejemplo del tema de la Binomial.

---

Instrucciones en Python

# Proceso caminata de pasos aleatorios
# Leon-Garcia E 9.14 p.500
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
# n=int(input('cuantos aleatorios: '))
# p=float(input('probabilidad p: '))
n = 20
p = 0.5

# PROCEDIMIENTO

# inicializa vectores
pasos  = np.zeros(n, dtype=int)
camina = np.zeros(n, dtype=int)
ejex   = np.zeros(n, dtype=int)

s = 0 
for i in range(0,n):
    # genera aleatorio con binomial
    pasos[i] = 2*(stats.binom.rvs(1,p))-1
    s = s+pasos[i]
    camina[i] = s
    ejex[i]   = i

# SALIDA
# grafica pasos 
plt.subplot(211)
plt.stem(ejex,pasos)
plt.ylabel('Pasos Dn')
plt.margins(0.05)

# grafica caminata aleatoria
plt.subplot(212)
plt.stem(ejex,camina)
plt.ylabel('Caminata Sn')
plt.margins(0.05)
plt.xlabel('n')

plt.show()

Referencia: León-García 9.14 p.500-501

La forma mas simple de un proceso aleatorio – independiente, con secuencias identicamente distribuidas (iid).

Procesos aleatorios iid

La secuencia X_n de un proceso aleatorio iid consiste en una secuencia de variables independientes, identicamente distribuidas con cdf F_x(x), media m y varianza σ² .

mX(n) = E[Xn] = m     para todo n

lo que indica que su media es constante.

La función de autocovarianza , si n₁ ≠ n₂ :

Cx(n1, n2) = E[(Xn1 - m)(Xn2 - m)] =
= E[(Xn1 - m)] E[(Xn2 - m)] = 0       

dado que X_n1 y X_n2 son variables independientes y si n₁ = n₂ = n:

Cx(n1, n2) = E[(Xn - m)2] = σ2 

lo que permite expresarla como:

Cx(n1, n2) = σ2 δn1n2

donde δ_n1n2 = 1 si n₁ = n₂ y 0 para cualquier otro caso, que también expresa que su autocovarianza es cero en cualquier lugar exceptuando n₁ = n₂.

La función de autocorrelación de un proceso iid es:

Rx(n1, n2) = Cx(n1, n2) + m2

Ejemplo: Proceso aleatorio Bernoulli

Leon-García E9.13 pdf/p.499

La secuencia I_n es una secuencia de variable aleatoria independiente tipo Bernoulli.
Una ejecución se muestra en a figura. Se puede interpretar como el evento que un foco falle y se reemplace en un dia n.

tiene media y varianza:

m1 = p     VAR[In] = p(1-p)

permite realizar cálculos de forma muy sencilla, por ejemplo, la probabilidad que los primeros cuatro bits tengan la secuencia 1001

p[I1=1,I2=0,I3=0,I4=1] = 
= p[I1=1]p[I2=0]P[I3=0]P[I4=1]=
= p2(1-p)2

o que la probabilidad de que el segundo bit sea 0 y el septimo sea 1

P[I2=0, I7=1] = P[I2=0]P[I7=1] = p(1-p)

El código python para generar el proceso bernoulli usado es:

% matplotlib inline
# Generar numeros aleatorios con distribución bernoulli
# Leon-Garcia E9.13 Proceso aleatorioBernoulli 
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
# n=int(input('cuantos aleatorios: '))
# p=float(input('probabilidad p: '))
n=20
p=0.5

# Procedimiento
pasos=np.zeros(n, dtype=int)
camina=np.zeros(n, dtype=int)

# procesa los datos
s=0
for i in range(0,n):
    pasos[i]=stats.binom.rvs(1,p)
    s=s+pasos[i]
    camina[i]=s

# SALIDA
plt.subplot(211)
plt.stem(pasos)
plt.ylabel('bernoulli In')
plt.margins(0.05)

plt.subplot(212)
plt.stem(camina)
plt.ylabel('Sn')
plt.margins(0.05)
plt.show()

Distribuciones conjuntas de muestras en el tiempo

Sean [X₁, X₂, … , X_k ] las k variables aleatorias obtenidas del muestreo de un proceso X(t,ω) en los tiempos: [t₁, t₂, … , t_k] se describen como:

X₁ = X(t₁,ω),
X₂ = X(t₂,ω),
… ,
X_k = X(t_k,ω),

mostrada en la figura:

El comportamiento conjunto del proceso aleatorio a estos k instantes de tiempo se da por la distribución acumulada conjunta del vector de las variables aleatorias :
X₁, X₂, … , X_k

Las probabilidades de cualquiera de los eventos del proceso aleatorio para todos o solo algunos de los instantes de tiempo, se pueden calcular por medio de la distribucion acumulada (cdf) con los metodos para vectores de variables aleatorias.

Por lo que un proceso aleatorio o estocástico se especifica por la colección de k-ésimo orden de las funciones de distribución acumuladas conjuntas :

$F_{x_1, ... , x_k}(x_1, x_2, ... , x_k)=P[X_1 ≤ x_1, X_2 ≤ x_2, ... , X_k≤ x_k]$

para cualquier k y cualquier selección de instantes de tiempo t₁, t₂, … , t_k.

Si el proceso estocástico es de valores contínuos, entonces las funciones de densidad de probabilidad a usar serán:

$f_{x_1, ... , x_k}(x_1, x_2, ... , x_k) dx_1 ... dx_n =$ $P[x_1 < X_1 ≤ x_1+dx_1, x_2 < X_2 ≤ x_2+dx_2, ... , x_k < X_k ≤ x_k+dx_1]$

Si el proceso estocastico es de tipo discreto, entonces la colección de funciones de probabilidad de masa para especificar el proceso estocastico será:

$p_{x_1, ... , x_k}(x_1, x_2, ... , x_k) =$ $P[ X(t_1) = x_1, X(t_2) = x_2, ... , X(t_k) = x_k ]$

---

Ejemplo: Variable aleatoria Bernoulli iid

Referencia: León García E9.5 pdf/p.492

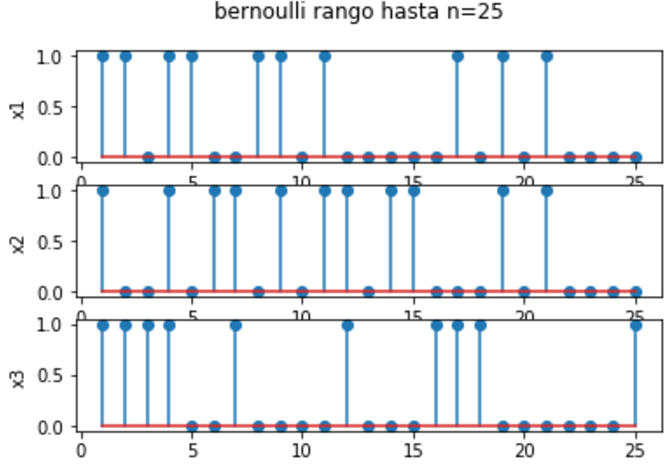
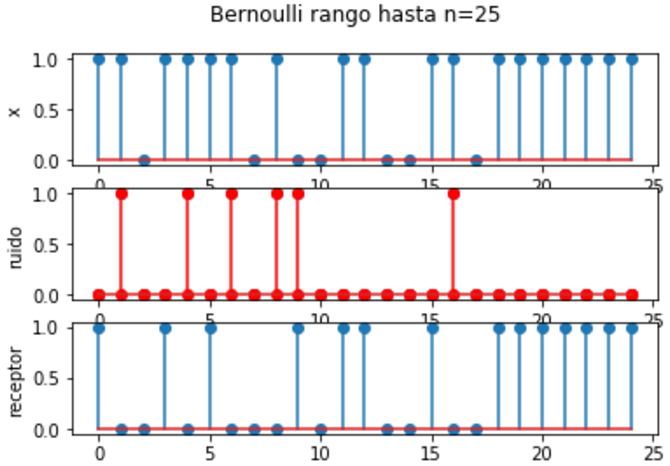
Sea X_n una secuencia de una variable aleatoria independiente e identicamente distribuida(i.i.d), tipo Bernoulli con p=1/2.
La pmf conjunta para cualquier k muestras de tiempo es entonces:

P[ X₁ = x₁, X₂ = x₂, … , X_k = x_k ] =
= P[ X₁ = x₁] P[X₂ = x₂], … , P[X_k = x_k ]
= (1/2)^k

donde x_i ∈ {0,1] para todo i.

Ejemplo: Variable aleatoria Gausiana iid

Referencia: León García E9.6 pdf/p.493

Sea X_n una secuencia de una variable aleatoria independiente e identicamente distribuida (i.i.d.), tipo Gausiana con media μ=0 y varianza σ²_x. La función de densidad de probabilidad (pdf) conjunta para cualquier muestra de tiempo k es entonces:

$f_{x_1,x2, ...,x_k}(x_1,x2, ...,x_k)=$ $= \frac{1}{(2\pi \sigma^2)^{k/2}}e^{-(x_1^2+x_2^2+ ... + x_k^2)/2\sigma^2}$

Ejemplo: Proceso Binomial de conteo

Referencia: León García E9.7 pdf/p.493

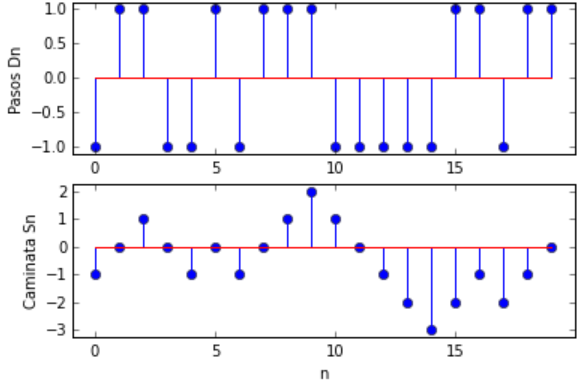
Sea X_n una secuencia de una variable aleatoria independiente e identicamente distribuida, tipo Bernoulli con p=1/2. Sea S_n el número de 1’s en los primeros n intentos:

S_n = X₁ + X₂ + … + X_n para n=0,1,…

S_n es una función de n valores enteros crecientes que aumenta en valores unitarios siguiendo intervalos de tiempo aleatorios.

---

Instrucciones en Python

para Distribuciones conjuntas de muestras en el tiempo

# Realizaciones de un proceso aleatorio
# León-García Fig 9.1
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
n = 50 # muestras
A = 10 # amplitud
k = 10 # una muestra k<n

# PROCEDIMIENTO
t = np.arange(0,n,1)
# genera variables aleatorias continuas uniformes
x1 = stats.uniform.rvs(loc=-A, scale=2*A ,size=n)
x2 = stats.uniform.rvs(loc=-A, scale=2*A ,size=n)
x3 = stats.uniform.rvs(loc=-A, scale=2*A ,size=n)

# SALIDA
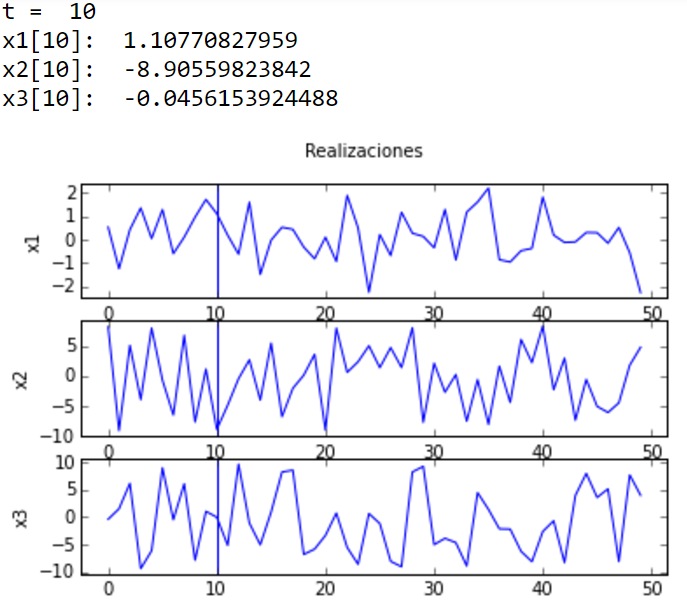
print('t = ',k)
print('x1['+str(k)+']: ', x1[k])
print('x2['+str(k)+']: ', x2[k])
print('x3['+str(k)+']: ', x3[k])

# GRAFICAS
plt.suptitle('Realizaciones')

# grafica X1
plt.subplot(311)
plt.plot(t,x1)
plt.axvline(10)
plt.ylabel('x1')
plt.margins(0.05)

# grafica X2
plt.subplot(312)
plt.plot(t,x2)
plt.axvline(10)
plt.ylabel('x2')
plt.margins(0.05)

# grafica X3
plt.subplot(313)
plt.plot(t,x3)
plt.axvline(10)
plt.ylabel('x3')
plt.margins(0.05)

plt.show()

Referencia: León-García 9.1 pdf/p.492

Un proceso aleatorio o proceso estocástico es una familia de variables aleatorias.

Por ejemplo, al enviar una secuencia de bits sobre un canal inalámbrico, no existe un grupo predeterminado de bits a transmitir, que para modelar se usa una secuencia infinita de variables aleatorias.

Tres realizaciones de X₁, X₂, … se obtienen como:

Instrucciones en Python

# secuencia de bits (trama)
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# ingreso
n = 25 
p = 0.5

# PROCEDIMIENTO
# indice k
k  = np.arange(1, n+1)

# genera muestras de variable aleatoria con bernoulli
x1 = stats.bernoulli.rvs(p, size=n)
x2 = stats.bernoulli.rvs(p, size=n)
x3 = stats.bernoulli.rvs(p, size=n)

# SALIDA
plt.suptitle('bernoulli rango hasta n='+str(n))

# grafica X1
plt.subplot(311)
plt.stem(k,x1)
plt.ylabel('x1')
plt.margins(0.05)

# grafica X2
plt.subplot(312)
plt.stem(k,x2)
plt.ylabel('x2')
plt.margins(0.05)

# grafica X3
plt.subplot(313)
plt.stem(k,x3)
plt.ylabel('x3')
plt.margins(0.05)

plt.xlabel('k')
plt.show()

---

Procesos discretos en el tiempo

Un proceso aleatorio discreto en el tiempo es una familia de variables aleatorias {X_n}, donde a partir de n se define en un subgrupo de enteros.

Por ejemplo:

{X_n, n=1, 2, …}

{X_n, n=0, 1, 2, …}

{X_n, n=0, ± 1 , ± 2 …}

Recordando que las variables aleatorias son funciones definidas en un espacio muestral S, se puede pensar en X_n(ω) en dos formas:

• • Para n fijos, X_n(ω) es función de ω y por lo tanto una variable aleatoria.
  • Para ω fija, se obtiene una secuencia de números X₁(ω), X₂(ω), X₃(ω), … . Secuencia que se denomina una realización, camino muestral, o función muestral del proceso aleatorio.

Ejemplo: Envío de bits sobre un canal con ruido

Referencia: Gubner 10.1 pdf/p.383

Enviar una secuencia de bits sobre un canal con ruido , los bits se invierten de forma independiente con probabilidad p.

Sea:

• • • • X_n(ω)=1 si se invierte el n-ésimo bit y
      • X_n(ω)=0 de otra forma.

entonces {X_n(ω), n= 1, 2, …} es una secuencia Bernoulli(p) i.i.d .

Tres realizaciones del ruido se reprerentan en la gráfica del ejercicio anterior. Sin embargo, el resultado de la señal X_n afectada por el Ruido_n como se vería en el receptor se muestra a continuación.

# Ejercicio: Envío de bits sobre un canal con ruido
# Gubner 10.1 
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
n = 25 
pcanal = 0.5
p = 0.2 # error o inversión de bit

# PROCEDIMIENTO
# muestras k
k  = np.arange(1, n+1)

# transmisor
x     = stats.bernoulli.rvs(pcanal, size=n)
# ruido del canal
ruido = stats.bernoulli.rvs(p, size=n)

# En el receptor
receptor = np.zeros(len(x), dtype = int)
for i in range(0,len(x)):
    if (ruido[i] == 0):
        receptor[i] = x[i]
    if (ruido[i] == 1):
        # invierte el bit
        if (x[i] == 1):
            receptor[i] = 0
        if (x[i] == 0):
            receptor[i] = 1

# SALIDA
plt.suptitle('Bernoulli rango hasta n='+str(n))

# trama de bits en transmisor
plt.subplot(311)
plt.stem(k,x)
plt.ylabel('x')
plt.margins(0.05)

# ruido del canal
plt.subplot(312)
plt.stem(k,ruido,markerfmt='or')
plt.ylabel('ruido')
plt.margins(0.05)

# Señal recibida en receptor
plt.subplot(313)
plt.stem(k,receptor)
plt.ylabel('receptor')
plt.margins(0.05)

plt.xlabel('k')
plt.show()

---

Procesos contínuos en el tiempo

Un proceso aleatorio contínuo en el tiempo es una familia de variables aleatorias {X_t} donde t esta definido en un intervalo de tiempo.

{X_t, t ≥ 0}
{X_t, 0 ≤ t ≤ T}
{X_t, -∞ ≤ t ≤ ∞}

Ejemplo: Portadora con fase aleatoria

Referencia: Gubner 10.5 pdf/p.386

En radio comunicación, una señal portadora se modela como una sinusoide con fase aleatoria. La razón para usar una fase aleatoria es que en receptor no se conoce cuando se encendió el transmisor o la distancia entre el transmisor y receptor, que son factores que afectan a la fase.

El modelo matemático para éste caso es el proceso aleatorio contínuo en el tiempo, definido por:

x_t = cos(2πft + θ)

donde f es la frecuencia de la portadora y θ es una variable aleatoria uniforme [-π, π].

Tres realizaciones del proceso que dan tres valrores dirferenctes de θ y su efecto en la portadora se obtienen como:

# Gubner 10.5 Portadora con fase aleatoria
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# ingreso
n = 5
f = 1

# PROCEDIMIENTO
# muestras ti
t = np.arange(0,n,0.1)

# genera muestras aleatorias con f: uniforme
theta = stats.uniform.rvs(loc=-np.pi, scale=2*np.pi ,size=3)

# selales desfasadas
xt0 = np.cos(2*np.pi*f*t + theta[0])
xt1 = np.cos(2*np.pi*f*t + theta[1])
xt2 = np.cos(2*np.pi*f*t + theta[2])

# SALIDA
print('theta: ',theta)

# grafica
plt.suptitle('Portadora')
# grafica x0
plt.subplot(311)
plt.plot(t,xt0)
plt.ylabel('x0')
plt.margins(0.05)

# grafica x1
plt.subplot(312)
plt.plot(t,xt1)
plt.ylabel('x1')
plt.margins(0.05)

# grafica x2
plt.subplot(313)
plt.plot(t,xt2)
plt.ylabel('x2')
plt.margins(0.05)

plt.xlabel('k')
plt.show()

Referencia: Gubner 10 pdf/p.383, León-García 9.1 pdf/p.488