Proyectos realizados o en desarrollo sobre tecnologías inalámbricas, plataformas tecnológicas.

Grupo de Investigación de Redes de iNformación Inalámbricas
Proyectos realizados o en desarrollo sobre tecnologías inalámbricas, plataformas tecnológicas.
Una revisión del modelo de propagación encontrado con los puntos de entrenamiento se puede realizar con puntos de prueba. Las lecturas de los puntos de prueba se realizaron dos semanas después de los puntos de entrenamiento.
Los puntos de prueba tienen una lectura a cada baliza, a diferencia de al menos cien de los puntos de entrenamiento.
En la revisión se encuentra que los puntos de prueba se encuentran en el rango de las mediciones del modelo, sin embargo los puntos se encuentran distribuidos en la gráfica desplazados hacia arriba del modelo, indicando que es necesario incorporar más variables para ajustar el modelo, por ejemplo la temperatura del entorno u otra variable que se determinaría en una siguiente fase del experimento.
Para cuantificar el desplazamiento Δrssi, se calcula el error entre cada punto y la ecuación modelo. Bajo el concepto que los errores se distribuyen equitativamente sobre y debajo la ecuación, se obtiene el valor de la mediana que indica el desplazamiento más optimo como ajuste al modelo bajo las nuevas condiciones.
Revisando la aplicabilidad del modelo, se obtiene el coeficiente de correlación para los puntos de prueba clasificados en gtwFIEC, que es de -0.88 que permite estimar que se puede aplicar relación lineal con pendiente negativa en el intervalo.
gtwFIEC s0 r0 error_mediana: 5.99 correlacion: -0.88 gtwFIEC s0 r1 error_mediana: 7.14 correlacion: -0.68 gtwFIEC s0 r2 error_mediana: 1.98 correlacion: -0.76
Se puede proseguir con los otros puntos de prueba para las otras balizas, encontrando que en la baliza gtwRECT los mejores valores de correlación con los datos disponibles tan dado en el área de vegetación sin sombra. El modelo estimado en vegetación para la zona con sombra debe ser revisados pues hay un valores cercanos a cero en correlación, por lo que la linealización con los datos puede ser insuficiente para estimar que hay una relación lineal entre las dos variables. Se requiere en ese caso expandir la toma de muestra y revisar con mas datos el modelo.
Desplazamientos de puntos de prueba respecto al modelo: [baliza,sector,intervalo,drssi] gtwRECT s0 r0 error_mediana: 7.8 correlacion: -0.54 gtwRECT s0 r1 error_mediana: 5.55 correlacion: -0.13 gtwRECT s0 r2 error_mediana: 9.3 correlacion: -0.47 gtwRECT s1 r0 error_mediana: 3.7 correlacion: 0.13 gtwRECT s1 r1 error_mediana: 3.7 correlacion: 0.13 gtwFIEC s0 r0 error_mediana: 5.99 correlacion: -0.88 gtwFIEC s0 r1 error_mediana: 7.14 correlacion: -0.68 gtwFIEC s0 r2 error_mediana: 1.98 correlacion: -0.76 gtwFCNM s0 r0 error_mediana: 8.56 correlacion: -0.76 gtwFCNM s0 r1 error_mediana: 6.59 correlacion: -0.75 gtwFCNM s0 r2 error_mediana: 9.98 correlacion: -0.29
Se adjunta el algoritmo correspondiente:
# LoRa-Multipunto, Revisa grafica Rssi vs distancia # con puntos de prueba 'CIRC' # linealización Rssi vs log10(distancia) por mínimos cuadrados # Graficas 2D y 3D # Girni 2020-01-30 propuesta: edelros@espol.edu.ec import numpy as np import pandas as pd import json import matplotlib.pyplot as plt import girni_lora_libreria as girni # INGRESO # archivos de entrada modo = 'rx' medida = 'rssi' descriptor = 'mean' arch_ecuaciones = 'rsmP07_ecuacionSector01.json' arch_medidaubica = 'rsmP06_'+medida+'UbicaCirc01.txt' # archivos de salida arch_ecuaciones2 = 'rsmP07_ecuacionSector02.json' baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} # Parámetros de grafica tipograf = '2D' # '2D','3D' escala = 'log' # 'normal','log' escalabase = 10 # 10, np.exp() casicero = 1e-4 precision = 2 intersectar = 0 # 0:Falso, 1: Verdadero # Referencias de gráfica grupo = ['FIEC' ,'FCNM' ,'RECT','CIRC'] colores = ['green','orange','grey','magenta'] tipo = ['punto','1m' ,'gtw','dispositivo'] marcas = [ 'o','D' ,'D' ,'*' ] mostrargrpeti = ['FIEC','FCNM','RECT'] mostrartipeti = ['1m','gtw'] # PROCEDIMIENTO # leer datos with open(arch_ecuaciones) as json_file: ecuacion = json.load(json_file) tabla = pd.read_csv(arch_medidaubica, index_col='etiqueta') tabla = pd.DataFrame(tabla) baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) eq_graf = {} # Revisa un sector_estimado for cualbaliza in baliza: sector_baliza = 'sector_'+cualbaliza tabla[sector_baliza] = 0 for cadapunto in tabla.index: for cualbaliza in baliza: # evalua en sector sector_baliza = 'sector_'+cualbaliza donde = baliza_key.index(cualbaliza) # coordenadas baliza para identificar ángulo b_este = tabla['c_este'][baliza[cualbaliza]] b_norte = tabla['c_norte'][baliza[cualbaliza]] # coordenadas del punto p_este = tabla['c_este'][cadapunto] p_norte = tabla['c_norte'][cadapunto] dx = p_este-b_este dy = p_norte-b_norte theta = np.arctan2(dy,dx) if theta<0: theta = theta + 2*np.pi sectores = ecuacion[baliza[cualbaliza]]['sector_rad'] nsectores = len(sectores) otrosector = '' for i in range(0,nsectores-1,1): a = sectores[i] b = sectores[i+1] if theta>=a and theta<b: otrosector = i+1 if otrosector !='': tabla.loc[cadapunto,'sector_'+cualbaliza] = otrosector # analiza datos hacia una baliza for unabaliza in ecuacion: donde = baliza_val.index(unabaliza) cualbaliza = baliza_key[donde] eq_graf[unabaliza] = {} for unsector in list(ecuacion[unabaliza].keys()): if unsector != 'sector_rad': eq_graf[unabaliza][unsector] = {} for i_eq in list(ecuacion[unabaliza][unsector].keys()): eq_graf[unabaliza][unsector][i_eq] = {} # puntos de tabla for unsector in list(ecuacion[unabaliza].keys()): if unsector != 'sector_rad': xi_p = [] ; yi_p = [] xi = [] ; yi = [] ; etiqueta = [] columna = medida+'_'+modo+'_'+cualbaliza for cadapunto in tabla.index: p_rssi = np.round(tabla[columna][cadapunto], precision) dist = np.round(tabla['dist_'+cualbaliza][cadapunto], precision) ensector = 's'+str(tabla['sector_'+cualbaliza][cadapunto]) LOS = tabla['LOS_'+cualbaliza][cadapunto] if not(np.isnan(p_rssi)) and dist>1 and LOS==1 and unsector==ensector: yi_p.append(p_rssi) xi_p.append(dist) etiqueta.append(cadapunto) if not(dist in xi): xi.append(dist) yi.append(p_rssi) xi_p = np.array(xi_p) yi_p = np.array(yi_p) ordenar = np.argsort(xi_p) xi_p = list(xi_p[ordenar]) yi_p = list(yi_p[ordenar]) etiqueta = np.array(etiqueta) etiqueta = etiqueta[ordenar] xi = np.array(xi) yi = np.array(yi) ordenar = np.argsort(xi) xi = xi[ordenar] yi = yi[ordenar] i_eq = 'r0' # todos los puntos eq_graf[unabaliza][unsector][i_eq]['xi'] = xi_p.copy() eq_graf[unabaliza][unsector][i_eq]['yi'] = yi_p.copy() eq_graf[unabaliza][unsector][i_eq]['etiqueta'] = etiqueta.copy() # ecuacion linealizada for i_eq in list(ecuacion[unabaliza][unsector].keys()): a = ecuacion[unabaliza][unsector][i_eq]['intervalox'][0] b = ecuacion[unabaliza][unsector][i_eq]['intervalox'][1] alpha = ecuacion[unabaliza][unsector][i_eq]['alpha'] beta = ecuacion[unabaliza][unsector][i_eq]['beta'] std = ecuacion[unabaliza][unsector][i_eq]['error_std'] fdist = lambda d: -10*alpha*(np.log10(d))+beta subintervalo = (xi >= a) & (xi <= b) xi_s = xi[subintervalo] yi_s = yi[subintervalo] # correlacion de los puntos correlacion = np.corrcoef(xi_s,yi_s)[0,1] # dibujar la línea en intervalo xi_sub = xi[subintervalo] if not(a in xi_sub): xi_sub = np.concatenate(([a],xi_sub),axis=0) if not(b in xi_sub): xi_sub = np.concatenate((xi_sub,[b]),axis=0) yi_sub = fdist(xi_sub) eq_graf[unabaliza][unsector][i_eq]['xi_graf'] = xi_sub.copy() eq_graf[unabaliza][unsector][i_eq]['yi_graf'] = yi_sub.copy() # Errores en subintervalo mediana = 0 if intersectar == 0: yie_s = yi_s - fdist(xi_s) mediana = np.median(yie_s) else: if i_eq=='r0': yie_s = yi_s - fdist(xi_s) mediana = np.median(yie_s) else: mediana = ecuacion[unabaliza][unsector]['r0']['desplaza'] eq_graf[unabaliza][unsector][i_eq]['desplaza'] = mediana eq_graf[unabaliza][unsector][i_eq]['correlacion'] = correlacion ecuacion[unabaliza][unsector][i_eq]['desplaza'] = mediana # SALIDA print('Desplazamientos de puntos de prueba') print(' respecto al modelo:') print('[baliza,sector,intervalo,drssi]') for unabaliza in ecuacion: for unsector in list(ecuacion[unabaliza].keys()): if unsector != 'sector_rad': for i_eq in list(ecuacion[unabaliza][unsector].keys()): mediana = ecuacion[unabaliza][unsector][i_eq]['desplaza'] mediana = np.round(mediana,precision) correlacion = eq_graf[unabaliza][unsector][i_eq]['correlacion'] correlacion = np.round(correlacion,precision) texto = unabaliza + ' '+unsector + ' ' + i_eq + ' ' texto = texto + ' error_mediana: '+ str(mediana) texto = texto + ' correlacion: '+str(correlacion) print(texto) # salida hacia archivo with open(arch_ecuaciones2, 'w') as outfile: json.dump(ecuacion, outfile) # GRAFICA # Referencias para gráfica grupo = ['FIEC' ,'FCNM' ,'RECT','CIRC'] colores = ['green','orange','grey','magenta'] tipo = ['punto','1m' ,'gtw','dispositivo'] marcas = [ 'o','D' ,'D' ,'*' ] mostrargrpeti = ['FIEC','FCNM','RECT'] mostrartipeti = ['1m','gtw'] if tipograf=='2D': for unabaliza in eq_graf: for unsector in eq_graf[unabaliza]: figura,grafica = plt.subplots() if escala == 'log': grafica.set_xscale(escala,base=escalabase) eq_graf2 = {} # todos los puntos unintervalo = 'r0' xi_p = eq_graf[unabaliza][unsector][unintervalo]['xi'] yi_p = eq_graf[unabaliza][unsector][unintervalo]['yi'] etiqueta = eq_graf[unabaliza][unsector][unintervalo]['etiqueta'] grafica.scatter(xi_p,yi_p,marker='.') m = len(xi_p) for i in range(0,m,1): grafica.annotate(etiqueta[i], (xi_p[i],yi_p[i])) # linea con todos los puntos for i_eq in list(eq_graf[unabaliza][unsector].keys()): fdtxt = ecuacion[unabaliza][unsector][i_eq]['eq_latex'] xi_graf = eq_graf[unabaliza][unsector][i_eq]['xi_graf'] yi_graf = eq_graf[unabaliza][unsector][i_eq]['yi_graf'] a = np.round(ecuacion[unabaliza][unsector][i_eq]['intervalox'][0],precision) b = np.round(ecuacion[unabaliza][unsector][i_eq]['intervalox'][1],precision) desplaza = eq_graf[unabaliza][unsector][i_eq]['desplaza'] desplaza = np.round(desplaza,precision) estilo = 'solid' if i_eq =='r0': estilo = 'dashed' eq_texto = i_eq+': '+fdtxt+' ; ['+str(a)+','+str(b)+']' grafica.plot(xi_graf,yi_graf, label = eq_texto, linestyle = estilo) # para linea desplazada eq_graf2[i_eq] = {'xi':xi_graf, 'yi':yi_graf + desplaza, 'desplaza': desplaza} # lineas de frontera grafica.axvline(a, color='lightblue') valor_frontera = str(np.round(a,precision)) grafica.annotate(valor_frontera, (a,np.max(yi_p)), color='lightblue') grafica.axvline(b, color='lightblue') valor_frontera = str(np.round(b,precision)) grafica.annotate(valor_frontera, (b,np.max(yi_p)), color='lightblue') for i_eq in list(ecuacion[unabaliza][unsector].keys()): estilo = 'solid' if i_eq =='r0': estilo = 'dashed' xi = eq_graf2[i_eq]['xi'] yi = eq_graf2[i_eq]['yi'] desplaza = eq_graf2[i_eq]['desplaza'] texto = i_eq + ' + $\Delta $Rssi' texto = texto + ' ; $ \Delta rssi$= '+ str(desplaza) grafica.plot(xi,yi, label = texto, linestyle = estilo) # etiquetas y títulos grafica.legend() grafica.set_ylabel(medida+'_'+modo) grafica.set_xlabel('distancia') grafica.grid(True,linestyle='dotted', axis='x', which='both') untitulo = unabaliza+' '+unsector+': Puntos de prueba desplazados' grafica.set_title(untitulo) plt.show()
El comportamiento de la señal de cada baliza hacia un punto en particular se observa al calcular algunos valores de estadística.
El valor principal para el modelo de localización usado es el promedio de rssi de cada baliza en el punto.
Otro valor comprementario la desviación estándar (std, σ) que es una medida de dispersión alrededor de la media. Estas variaciones estan asociadas a múltiples factores que depende de las características del entorno.

Si hay valores de promedios de un punto que son atípicos a la tendencia entre Rssi y la distancia se puede recurrir a ésta sección para observar el punto.
Con el algoritmo se obtienen los siguientes valores para el punto del ejemplo:
baliza: d1 gtwRECT muestras: 137 tramo: 17 count mean std min 25% 50% 75% max 0 118.0 -128.211864 1.960515 -132.0 -130.0 -128.5 -127.0 -123.0 baliza: d2 gtwFIEC muestras: 144 tramo: 15 count mean std min 25% 50% 75% max 0 118.0 -128.211864 1.960515 -132.0 -130.0 -128.5 -127.0 -123.0 baliza: d3 gtwFCNM muestras: 118 tramo: 9 count mean std min 25% 50% 75% max 0 118.0 -128.211864 1.960515 -132.0 -130.0 -128.5 -127.0 -123.0
El primer valor que se requiere es el nombre del punto, ejemplo 'FIEC102', luego el modo de lectura (rx,tx') y la medida (rssi, snr).
Los datos se toman del archivo que integra en una tbala los datos del punto, en formato json del proceso anterior.
Se usa el diccionario que identifica a las balizas para realizar la tabulación de los descriptores.
# INGRESO cadapunto = 'FIEC102' modo = 'rx' medida = 'rssi' descriptor = 'mean' # Archivos de datos arch_detalles = 'rsmP02_tabla_puntosdatos01.json' # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} tolera = 1e-8
Los resultados se complementan con la gráfica que muestra la distribución de probabilidad para cada baliza, marcando también el valor de promedio y la suma de promedio mas desvición estándar.
El análisis del comportamiento de la señal de cada punto tiene relación con el entorno del punto dominado por edificios o vegetación.
# Revisar un punto, descriptores estadísticos # requiere un punto, modo, medida # nombre del archivo de la tabla detalle # Girni 2020-10-07 edelros@espol.edu.ec import numpy as np import pandas as pd import json import matplotlib.pyplot as plt # INGRESO cadapunto = 'FIEC102' modo = 'rx' medida = 'rssi' descriptor = 'mean' # Archivos de datos arch_detalles = 'rsmP02_tabla_puntosdatos01.json' # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} tolera = 1e-8 # PROCEDIMIENTO baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) # leer datos with open(arch_detalles) as json_file: puntodato = json.load(json_file) punto = {} for cadabaliza in baliza: punto[cadabaliza] = {} # revisa un punto unpunto = puntodato[modo][cadapunto][cadabaliza][medida+'_'+modo] unpunto = np.array(unpunto) ordenar = np.argsort(unpunto) unpunto = unpunto[ordenar] puntopd = pd.DataFrame(unpunto) describe = puntopd.describe() describe = describe.T pmin = describe['min'][0] pmax = describe['max'][0] tramo = int(pmax-pmin) conteo = np.zeros(tramo+1,dtype=int) posicion = np.arange(pmin,pmax+1,1) posicion = list(posicion) conteo = list(conteo) for valor in unpunto: donde = posicion.index(valor) conteo[donde] = conteo[donde] + 1 punto[cadabaliza] = {'muestras': len(unpunto), 'tramo': tramo, 'posicion': posicion.copy(), 'conteo': conteo.copy(), 'describe': describe} # SALIDA for cadabaliza in baliza: print('baliza:', cadabaliza, baliza[cadabaliza]) print('muestras: ', punto[cadabaliza]['muestras'], 'tramo: ' , punto[cadabaliza]['tramo']) print(describe) # grafica precision = 2 figura,grafica = plt.subplots() n_baliza = len(baliza) for cadabaliza in baliza: p_media = np.round(punto[cadabaliza]['describe']['mean'][0],precision) p_std = np.round(punto[cadabaliza]['describe']['std'][0],precision) muestras = punto[cadabaliza]['muestras'] posicion = punto[cadabaliza]['posicion'] conteo = np.array(punto[cadabaliza]['conteo'])/muestras conteomax = np.max(conteo) #grafica.plot(posicion,conteo,'o',label = cadabaliza) grafica.plot(posicion,conteo,'-',label = cadabaliza) grafica.axvline(p_media, color = 'green', linestyle = 'dashed') texto = cadabaliza + ': ' + str(p_media) grafica.annotate(cadabaliza+': '+str(p_media),(p_media,conteomax), color='green') grafica.axvline(p_media+ p_std, color ='orange', linestyle = 'dotted') texto = texto + '+' + str(p_std) grafica.annotate(texto,(p_media+p_std,conteomax-0.015), color='orange') grafica.axvline(p_media- p_std, color ='orange', linestyle = 'dotted') grafica.axvline(p_media+ 2*p_std, color ='yellow', linestyle = 'dotted') grafica.axvline(p_media- 2*p_std, color ='yellow', linestyle = 'dotted') grafica.set_xlabel('rssi') grafica.set_ylabel('pmf') texto = 'Distribución de probabilidad: '+cadapunto+' '+medida grafica.set_title(texto) grafica.grid(True,linestyle='dotted', axis='y', which='both') grafica.legend() plt.show()
Para revisar los resultados de un solo punto, de todos los resultados anteriores, se realiza una gráfica que muestre los círculos de cada baliza con los radios de las distancias estimadas.
La gráfica permite observar los detalles de trilateración para ese punto en particular.
Resultados: baricentro: [ 614804.97 9762762.46] bar_error: 72.84 poligono x: [614760.66 614776.52 614877.73] poligono y: [9762742.69 9762778.91 9762765.77]
Por ejemplo para el caso del punto 'FIEC130' del que no se registró señal desde 'gtwFCNM' se tiene:
# trilaterando - gráfica de un punto # Girni 2020-10-07 propuesta: edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import pandas as pd import girni_lora_libreria as girni # INGRESO cadapunto = 'FIEC111' modo = 'rx' medida = 'rssi' arch_trilatera = 'rsmP07_'+medida+'trilateraSector01.txt' # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} tolera = 1e-8 # PROCEDIMIENTO baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) # leer datos tabla = pd.read_csv(arch_trilatera, index_col='etiqueta') tabla = pd.DataFrame(tabla) # Revisa indices existe = 0 if cadapunto in tabla.index: # coordenadas de baliza coordbaliza = {} for cadabaliza in baliza: cualbaliza = baliza[cadabaliza] coordbaliza[cadabaliza] = [tabla['c_este'][cualbaliza]] coordbaliza[cadabaliza].append(tabla['c_norte'][cualbaliza]) existe = 1 # coordenadas GPS del punto c_este = tabla['c_este'][cadapunto] c_norte = tabla['c_norte'][cadapunto] # coordenadas por trilateración punto = {} ubicados = np.zeros(4,dtype=int) for i in range(0,3,1): punto[i] = {} cuenta = 0 for unabaliza in baliza: punto[i][unabaliza] = tabla['dist'+str(i)+'_'+unabaliza][cadapunto] # si existe distancia if not(np.isnan(punto[i][unabaliza])): cuenta = cuenta + 1 if cuenta>0: ubicados[3]= ubicados[3] + 1 encontrado = tabla['encontrado'][cadapunto] if not(np.isnan(encontrado)): encontrado = int(encontrado) else: encontrado = 0 # trilatera el punto raiztodas = girni.intersectacirculos(punto[encontrado],coordbaliza,tolera) todasx = raiztodas[0] todasy = raiztodas[1] if len(todasx)>0: resultado = girni.trilatera(punto[encontrado],coordbaliza,tolera) # SALIDA precision=2 np.set_printoptions(precision) if existe ==1: if len(todasx)>0: print('intersectados: ') print(np.array(todasx)) print(np.array(todasy)) print('\nResultados: ') print('baricentro: ',np.array(resultado['baricentro'])) print('bar_error: ',np.round(resultado['barerror'],precision)) print('poligono x: ',np.array(resultado['poligono'][0])) print('poligono y: ',np.array(resultado['poligono'][1])) else: print('El punto indicado no existe') # Grafica if existe ==1: figura = plt.figure() grafica = figura.add_subplot(111) grafica.set_aspect('equal', adjustable='box') # punto con GPS texto = '['+str(np.round(c_este,2))+', '+str(np.round(c_norte,2))+']' grafica.scatter(c_este,c_norte, marker='D', color = 'grey', label = texto) grafica.annotate('gps',(c_este,c_norte), color ='grey') # cotas de gráfica unalista = list(coordbaliza.values()) unalista = np.array(unalista) cotax = [np.min(unalista[:,0]), np.max(unalista[:,0])] cotay = [np.min(unalista[:,1]), np.max(unalista[:,1])] cotadx = 0.15*(cotax[1]-cotax[0]) cotady = 0.15*(cotay[1]-cotay[0]) grafica.set_xlim(cotax[0]-cotadx,cotax[1]+cotadx) grafica.set_ylim(cotay[0]-cotady,cotay[1]+cotady) # raices k = len(todasx) if k>0: grafica.scatter(todasx,todasy, marker='+', color = 'magenta') poligono = resultado['poligono'] p = len(poligono[0]) for j in range(0,p,1): grafica.scatter(poligono[0][j],poligono[1][j], marker='*', color = 'blue') # coodenada con trilatera baricentro = resultado['baricentro'] sumabaricentro = np.sum(baricentro) if not(np.isnan(sumabaricentro)): texto = '['+str(np.round(baricentro[0],2)) texto = texto +', '+str(np.round(baricentro[1],2))+']' grafica.scatter(baricentro[0],baricentro[1], marker='D', color = 'red', label = texto) grafica.annotate('trilatera', (baricentro[0],baricentro[1]), color ='red') uncirculo = plt.Circle((baricentro[0],baricentro[1]), resultado['barerror'], ec = 'red', fc='None', linestyle ='dashed') grafica.add_artist(uncirculo) # circulos colores = ['blue','orange','lightgreen','grey'] j = 0 for fila in coordbaliza: xc = coordbaliza[fila][0] yc = coordbaliza[fila][1] r = punto[encontrado][fila] uncolor = colores[j] grafica.scatter(xc,yc, marker = '+', color = uncolor) grafica.annotate(fila,(xc,yc)) uncirculo = plt.Circle((xc,yc),r, ec = uncolor, fc='None', linestyle ='dotted') grafica.add_artist(uncirculo) j = j + 1 plt.title('Trilatera: ' + cadapunto) plt.legend() plt.xlabel('coordenada este') plt.ylabel('coordenada norte') plt.show()
Los sectores en una baliza se incorporan en el algoritmo como la estimación de ubicación del punto usando las otras balizas. 
Para un punto de ejemplo, dado que baliza 'gtwRECT' tiene sectores, se usan las otras balizas 'gtwFIEC' y 'gtwFCNM' para estimar la ubicación y el ángulo que permite aproximar el sector donde se ubicaría el punto.
Este sector se usa para aplicar la ecuación que corresponde al 'gtwFIEC'.
El desarrollo continua desde la sección anterior con solo intervalos y se incorpora el concepto.
# Localización por trilateración # Ubicación de puntos en el mapa # Girni 2020-10-07 propuesta: edelros@espol.edu.ec import numpy as np import sympy as sym import matplotlib.pyplot as plt import pandas as pd import json import girni_lora_libreria as girni # INGRESO # revisar parametros al inicio modo = 'rx' medida = 'rssi' # archivos de entrada arch_medUbAtrib = 'rsmP06_'+medida+'UbicaUsarSector01.txt' arch_ecuaciones = 'rsmP06_ecuacionSector01.json' # archivos de salida arch_trilatera = 'rsmP07_'+medida+'trilateraSector01.txt' # Parametros de grafica mostrargrp = ['FIEC'] #['FIEC','FCNM','RECT','CIRC'] mostrartip = ['punto'] mostrarfuera = [0,1] #[0,1] tolera_error = 2 # decimales en error # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} # Parámetros de grafica tipograf = '2D' # '2D','' sin grafica # PROCEDIMIENTO baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) # leer datos with open(arch_ecuaciones) as json_file: ecuacion = json.load(json_file) tabla = pd.read_csv(arch_medUbAtrib, index_col='etiqueta') tabla = pd.DataFrame(tabla) # coordenadas de baliza coordbaliza = {} for cadabaliza in baliza: cualbaliza = baliza[cadabaliza] coordbaliza[cadabaliza] = [tabla['c_este'][cualbaliza]] coordbaliza[cadabaliza].append(tabla['c_norte'][cualbaliza]) # inicializa ubicados,encontrados, intervalos fuera, errores # ubicados tiene [distancia, distancia+1s, distancia +2s,total] ubicados = np.zeros(shape=(3,4),dtype=int) tabla['interv_fuera'] = '' tabla['encontrado'] = np.nan tabla['ensector'] = '' # suma de errores sumatrilat = np.zeros(shape=(2,4),dtype=float) sumagps = np.zeros(shape=(2,4),dtype=float) sumagpsdx = np.zeros(shape=(2,4),dtype=float) sumagpsdy = np.zeros(shape=(2,4),dtype=float) # distancias y errores a cada baliza for unabaliza in baliza_val: donde = baliza_val.index(unabaliza) cualbaliza = baliza_key[donde] columna = medida+'_'+modo+'_'+cualbaliza tabla['dist0_'+cualbaliza] = np.nan tabla['dist1_'+cualbaliza] = np.nan tabla['dist2_'+cualbaliza] = np.nan # distancia estimada por punto for cadapunto in tabla.index: p_rssi = tabla[columna][cadapunto] esgrupo = tabla['grupo'][cadapunto] estipo = tabla['tipo'][cadapunto] unsector = 's0' if not(np.isnan(p_rssi)): ecuacion_rssi = ecuacion[unabaliza][unsector] if (esgrupo in mostrargrp) and (estipo in mostrartip): ubicados[2,donde] = ubicados[2,donde] + 1 dist = girni.dist_rssi(p_rssi,ecuacion_rssi) [distancia,e_mean,e_1std,e_2std,interv_fuera] = dist dist1 = distancia + e_1std dist2 = distancia + e_2std tabla.loc[cadapunto,'dist0_'+cualbaliza] = distancia tabla.loc[cadapunto,'dist1_'+cualbaliza] = dist1 tabla.loc[cadapunto,'dist2_'+cualbaliza] = dist2 if interv_fuera>0: if len(tabla['interv_fuera'][cadapunto])==0: separador='' else: separador=',' tabla.loc[cadapunto,'interv_fuera'] = tabla['interv_fuera'][cadapunto]+separador+cualbaliza procesados = np.max(ubicados[2,:]) # Revisa un sector_estimado columnas = list(tabla.keys()) for cadapunto in tabla.index: for cualbaliza in baliza: sector_baliza = 'sector_'+cualbaliza unsector = 0 if sector_baliza in columnas: unsector = tabla['sector_'+cualbaliza][cadapunto] if unsector!=0: # evalua en sector donde = baliza_key.index(cualbaliza) otrasbalizas = baliza_key.copy() otrasbalizas.pop(donde) # coordenadas de baliza coord_otrasbalizas = {} for cadaotrabaliza in otrasbalizas: cualotrabaliza = baliza[cadaotrabaliza] coord_otrasbalizas[cadaotrabaliza] = [tabla['c_este'][cualotrabaliza]] coord_otrasbalizas[cadaotrabaliza].append(tabla['c_norte'][cualotrabaliza]) # cada punto a i*std punto = {} sumabaricentro = np.nan for i in range(0,3,1): punto[i] = {} cuenta = 0 for cadaotrabaliza in otrasbalizas: punto[i][cadaotrabaliza] = tabla['dist'+str(i)+'_'+cadaotrabaliza][cadapunto] # si existe distancia if not(np.isnan(punto[i][cadaotrabaliza])): cuenta = cuenta + 1 # Hay 3 mediciones a baliza if cuenta==2: localiza = girni.trilatera(punto[i], coord_otrasbalizas, tolera = 10e-4) baricentro = localiza['baricentro'] barerror = localiza['barerror'] poligono = localiza['poligono'] sumabaricentro = np.sum(baricentro) if not(np.isnan(sumabaricentro)): break if not(np.isnan(sumabaricentro)): # coordenadas baliza para identificar ángulo b_este = tabla['c_este'][baliza[cualbaliza]] b_norte = tabla['c_norte'][baliza[cualbaliza]] # coordenadas del punto entre otras balizas p_este = baricentro[0] p_norte = baricentro[1] dx = p_este-b_este dy = p_norte-b_norte theta = np.arctan2(dy,dx) if theta<0: theta = theta + 2*np.pi sectores = ecuacion[baliza[cualbaliza]]['sector_rad'] nsectores = len(sectores) otrosector = '' for i in range(0,nsectores-1,1): a = sectores[i] b = sectores[i+1] if theta>=a and theta<b: otrosector = i+1 if otrosector !='': tabla.loc[cadapunto,'sector_'+cualbaliza] = otrosector # recalcula distancia con sector columna = medida+'_'+modo+'_'+cualbaliza p_rssi = tabla[columna][cadapunto] ecuacion_rssi = ecuacion[baliza[cualbaliza]]['s'+str(otrosector)] dist = girni.dist_rssi(p_rssi,ecuacion_rssi) [distancia,e_mean,e_1std,e_2std,interv_fuera] = dist dist1 = distancia + e_1std dist2 = distancia + e_2std tabla.loc[cadapunto,'dist0_'+cualbaliza] = distancia tabla.loc[cadapunto,'dist1_'+cualbaliza] = dist1 tabla.loc[cadapunto,'dist2_'+cualbaliza] = dist2 # trilateración. localiza cada punto # cada punto a i*std for i in range(0,3,1): tabla['trilat_este_'+str(i)] = np.nan tabla['trilat_norte_'+str(i)] = np.nan tabla['trilat_error_'+str(i)] = np.nan tabla['ubicado_'+str(i)] = np.nan tabla['trilat_gps_error_'+str(i)] = np.nan tabla['trilat_gps_dx_'+str(i)] = np.nan tabla['trilat_gps_dy_'+str(i)] = np.nan # procesa cada punto for cadapunto in tabla.index: esgrupo = tabla['grupo'][cadapunto] # coordenadas GPS del punto c_este = tabla['c_este'][cadapunto] c_norte = tabla['c_norte'][cadapunto] if esgrupo in mostrargrp: # cada punto a i*std punto = {} for i in range(0,3,1): punto[i] = {} cuenta = 0 for unabaliza in baliza: punto[i][unabaliza] = tabla['dist'+str(i)+'_'+unabaliza][cadapunto] # si existe distancia if not(np.isnan(punto[i][unabaliza])): cuenta = cuenta + 1 # Hay 3 mediciones a baliza if cuenta==3: localiza = girni.trilatera(punto[i], coordbaliza, tolera = 10e-4) baricentro = localiza['baricentro'] barerror = localiza['barerror'] poligono = localiza['poligono'] sumabaricentro = np.sum(baricentro) # Hay coordenadas de baricentro if not(np.isnan(sumabaricentro)): tabla.loc[cadapunto,'trilat_este_'+str(i)] = baricentro[0] tabla.loc[cadapunto,'trilat_norte_'+str(i)] = baricentro[1] tabla.loc[cadapunto,'trilat_error_'+str(i)] = np.round(barerror,tolera_error) # error trilatera hacia gps dx = baricentro[0] - c_este dy = baricentro[1] - c_norte error_gps = np.sqrt(dx**2+dy**2) tabla.loc[cadapunto,'trilat_gps_error_'+str(i)] = np.round(error_gps,tolera_error) tabla.loc[cadapunto,'trilat_gps_dx_'+str(i)] = np.round(dx,tolera_error) tabla.loc[cadapunto,'trilat_gps_dy_'+str(i)] = np.round(dy,tolera_error) # cuenta error si encuentra primera vez cond1 = np.isnan(tabla['encontrado'][cadapunto]) cond2 = len(tabla['interv_fuera'][cadapunto])>0 k = int(cond2) #intervalo extendido if cond1: tabla.loc[cadapunto,'encontrado'] = i ubicados[k,i] = ubicados[k,i]+1 sumatrilat[k,i] = sumatrilat[k,i] + np.round(barerror,tolera_error) sumagps[k,i] = sumagps[k,i] + np.round(error_gps,tolera_error) sumagpsdx[k,i] = sumagpsdx[k,i] + np.round(np.abs(dx),tolera_error) sumagpsdy[k,i] = sumagpsdy[k,i] + np.round(np.abs(dy),tolera_error) # contabiliza errores de localizados ubicasuma = np.zeros(2) ubicasumporc = np.zeros(2) ubicaporc = np.zeros(shape=(2,3)) for k in range(0,2,1): ubicados[k,3] = int(np.sum(ubicados[k,0:3])) ubicasuma[k] = np.sum(ubicados[k,0:3]) ubicasumporc[k] = np.round(100*ubicasuma[k]/ubicados[k,3],1) for i in range(0,3,1): ubicaporc[k,i] = np.round(100*ubicados[k,i]/ubicasuma[k],1) if ubicados[k,i]>0: sumatrilat[k,i] = np.round(sumatrilat[k,i]/ubicados[k,i],1) sumagps[k,i] = np.round(sumagps[k,i]/ubicados[k,i],1) sumagpsdx[k,i] = np.round(sumagpsdx[k,i]/ubicados[k,i],1) sumagpsdy[k,i] = np.round(sumagpsdy[k,i]/ubicados[k,i],1) # SALIDA print('Errores localizacion') import prettytable as ptt print('Errores estimado: Cota-Trilatera-polígono y Trilatera_vs_GPS') mostrar = ptt.PrettyTable(['punto','i*std','fuera','trilat', 'gps','gps_dx','gps_dy','sect_d1','sect_d2','sect_d3']) for cadapunto in tabla.index: # selecciona puntos a mostrar encontrado = tabla['encontrado'][cadapunto] esgrupo = tabla['grupo'][cadapunto] interv_fuera = int(len(tabla['interv_fuera'][cadapunto])!=0) cond1 = not(np.isnan(encontrado)) cond2 = esgrupo in mostrargrp cond3 = interv_fuera in mostrarfuera if cond1 and cond2 and cond3: encontrado = int(encontrado) mostrar.add_row([cadapunto, str(int(tabla['encontrado'][cadapunto])), tabla['interv_fuera'][cadapunto], str(tabla['trilat_error_'+str(encontrado)][cadapunto]), str(tabla['trilat_gps_error_'+str(encontrado)][cadapunto]), str(tabla['trilat_gps_dx_'+str(encontrado)][cadapunto]), str(tabla['trilat_gps_dy_'+str(encontrado)][cadapunto]), tabla['sector_d1'][cadapunto], tabla['sector_d2'][cadapunto], tabla['sector_d3'][cadapunto] ]) print(mostrar) print('puntos con medidas: ',procesados) loc_alg = np.round(100*np.sum(ubicados[:,3])/procesados,1) print('localizados con algoritmo: ', np.sum(ubicados[:,3]), ' , '+str(loc_alg)+'%' ) print('Errores Promedio:') resumen = ptt.PrettyTable(['error+i*std','cant','%','trilat', 'gps','gps_dx','gps_dy']) for k in range(0,2,1): if k == 0: texto = 'dentro' if k == 1: texto = 'fuera' resumen.add_row(['interv_'+texto,ubicados[k,3],'', '','','','']) for i in range(0,3,1): resumen.add_row(['error_'+str(i),ubicados[k,i], str(ubicaporc[k,i])+'%', sumatrilat[k,i],sumagps[k,i], sumagpsdx[k,i],sumagpsdy[k,i], ]) print(resumen) # salida hacia archivo tabla.to_csv(arch_trilatera) # Grafica ubicados ------------ # Referencias para gráfica grupo = ['FIEC' ,'FCNM' ,'RECT','CIRC'] colores = ['green','orange','grey','magenta'] tipo = ['punto','1m' ,'gtw','dispositivo'] marcas = [ 'o','D' ,'D' ,'*' ] colorstd = ['lightblue', 'lightgreen','orange'] colorlin = ['lightblue', 'lightgreen','orange'] if tipograf == '2D': figura,grafica = plt.subplots() # balizas for unabaliza in coordbaliza: g_este = coordbaliza[unabaliza][0] g_norte = coordbaliza[unabaliza][1] grafica.scatter(g_este,g_norte, color = 'red', marker = 'D', label = cadapunto) grafica.annotate(unabaliza, (g_este,g_norte)) # Puntos for cadapunto in tabla.index: g_este = tabla['c_este'][cadapunto] g_norte = tabla['c_norte'][cadapunto] # selecciona puntos a mostrar encontrado = tabla['encontrado'][cadapunto] esgrupo = tabla['grupo'][cadapunto] interv_fuera = int(len(tabla['interv_fuera'][cadapunto])!=0) cond1 = not(np.isnan(encontrado)) cond2 = esgrupo in mostrargrp cond3 = interv_fuera in mostrarfuera if cond1 and cond2 and cond3: encontrado = int(encontrado) p_este = tabla['trilat_este_'+str(encontrado)][cadapunto] p_norte = tabla['trilat_norte_'+str(encontrado)][cadapunto] grafica.scatter(p_este,p_norte, color = colorstd[encontrado], label = cadapunto) grafica.plot([p_este,g_este], [p_norte,g_norte], color = colorstd[encontrado], linestyle='dotted') grafica.scatter(g_este,g_norte, color = 'blue', label = cadapunto) grafica.annotate(cadapunto,(g_este,g_norte), color='blue') grafica.set_xlabel('UTM_este') grafica.set_ylabel('UTM_norte') grafica.grid() grafica.set_title('Puntos Ubicados') plt.show()
Al incorporar en los algoritmos el uso de sectores, se obtienen resultados con menores errores de localización, estimados por trilateración y respecto a las coordenadas del gps.
Se realiza un enfoque para el área de vegetación, 'FIEC', para comparar resultados
Los resultados numéricos resumen obtenidos son:
puntos con medidas: 21 localizados con algoritmo: 20 , 95.2% Errores Promedio: +---------------+------+--------+--------+------+--------+--------+ | error+i*std | cant | % | trilat | gps | gps_dx | gps_dy | +---------------+------+--------+--------+------+--------+--------+ | interv_dentro | 19 | | | | | | | error_0 | 8 | 42.1% | 53.5 | 34.7 | 27.9 | 17.5 | | error_1 | 8 | 42.1% | 55.8 | 46.4 | 37.7 | 22.9 | | error_2 | 3 | 15.8% | 72.2 | 51.6 | 30.4 | 34.0 | | interv_fuera | 1 | | | | | | | error_0 | 0 | 0.0% | 0.0 | 0.0 | 0.0 | 0.0 | | error_1 | 1 | 100.0% | 24.1 | 27.0 | 27.0 | 1.6 | | error_2 | 0 | 0.0% | 0.0 | 0.0 | 0.0 | 0.0 | +---------------+------+--------+--------+------+--------+--------+
Se observa que se tienen casi todos los puntos del área de vegetación ubicados. 'FIEC130' no se incorpora a la lista, pues no disponde de valores de Rssi para 'gtwFCNM'.
El detalle de los errores de localización de cada punto son:
Errores localizacion Errores estimado: Cota-Trilatera-polígono y Trilatera_vs_GPS +---------+-------+-------+--------+-------+--------+--------+---------+---------+---------+ | punto | i*std | fuera | trilat | gps | gps_dx | gps_dy | sect_d1 | sect_d2 | sect_d3 | +---------+-------+-------+--------+-------+--------+--------+---------+---------+---------+ | FIEC101 | 1 | d2 | 24.13 | 27.01 | -26.96 | -1.61 | 0 | 0 | 0 | | FIEC102 | 1 | | 58.51 | 39.76 | 19.4 | -34.71 | 0 | 0 | 1 | | FIEC103 | 1 | | 30.16 | 59.15 | 50.75 | -30.38 | 0 | 0 | 1 | | FIEC104 | 2 | | 85.75 | 71.3 | -14.25 | -69.86 | 0 | 0 | 0 | | FIEC105 | 0 | | 2.92 | 22.87 | -22.11 | 5.83 | 0 | 0 | 0 | | FIEC106 | 0 | | 59.12 | 23.54 | -14.24 | -18.74 | 0 | 0 | 0 | | FIEC107 | 1 | | 26.94 | 15.29 | -5.65 | 14.21 | 0 | 0 | 0 | | FIEC108 | 1 | | 70.86 | 30.08 | -22.52 | 19.94 | 0 | 0 | 1 | | FIEC109 | 1 | | 61.94 | 21.15 | 16.68 | 13.0 | 0 | 0 | 1 | | FIEC110 | 0 | | 40.85 | 26.49 | -20.07 | 17.29 | 0 | 0 | 0 | | FIEC111 | 0 | | 72.84 | 17.7 | 1.5 | -17.63 | 0 | 0 | 1 | | FIEC112 | 0 | | 51.21 | 36.32 | 34.6 | 11.06 | 0 | 0 | 1 | | FIEC115 | 2 | | 78.12 | 10.24 | -9.45 | 3.96 | 1 | 0 | 0 | | FIEC116 | 1 | | 57.3 | 91.81 | 90.07 | 17.76 | 1 | 0 | 1 | | FIEC117 | 2 | | 52.61 | 73.24 | 67.54 | 28.33 | 1 | 0 | 1 | | FIEC120 | 0 | | 120.27 | 40.98 | -40.4 | -6.86 | 1 | 0 | 0 | | FIEC121 | 0 | | 49.52 | 50.94 | 40.54 | 30.84 | 1 | 0 | 0 | | FIEC122 | 1 | | 66.97 | 56.82 | 41.11 | 39.23 | 1 | 0 | 1 | | FIEC123 | 0 | | 30.95 | 58.98 | 49.64 | 31.85 | 1 | 0 | 0 | | FIEC124 | 1 | | 73.54 | 57.4 | 55.58 | -14.33 | 1 | 0 | 0 | +---------+-------+-------+--------+-------+--------+--------+---------+---------+---------+
En el detalle se observa que solo para 'FIEC101' se usó un intervalo extendido de la ecuación hacia 'd2' que es 'gtwFIEC' estimando que es por encontrarse en los límites de la sección de vegetación.
El efecto "sombra" añade el parámetro sector a la ecuación que se incorpora al resultado de la linealización en cada baliza.
La ecuación de una baliza se compone entonces de dos parámetros de selección: sector e intervalo. 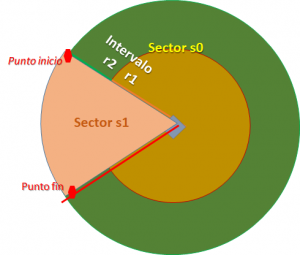
Como ilustración se muestra la figura que tiene tres partes o ecuaciones:
ecuacion['s0']['r1']
ecuacion['s0']['r2']
ecuacion['s1']['r0']
El primer parámetro para seleccionar la ecuación es el sector, 's0' y 's1', que en caso que sea un solo círculo se identifica como 's0'.
Dentro de cada sector, se mantiene el concepto de intervalos de distancia o radio. Se mantiene el concepto de la sección anterior, donde 'r0' corresponde a la linealización de todos los puntos en el sector. Cuando exiten sub-intervalos se usa 'r1', 'r2', etc para cada intervalo.
El número de ecuaciones corresponde al número de balizas y sectores establecidos para el análisis.
Se realizan cambios menores a la función pares_usar() de la librería girni para incorporar el parámetro sector, que al ser vacío '' funciona como fué descrito en las secciones anteriores.
pares_usar(tabla,baliza, analiza,unabaliza, unsector ='', medida = 'rssi', modo = 'rx')
También se actualizaron los nombres de los archivos de entrada y salida para diferenciar de los resultados anteriores y disponer de los archivos para comparar con los resultados del método que solo usa intervalos.
# LoRa-Multipunto, Rssi vs distancia con mínimos cuadrados # linealización Rssi vs log10(distancia) # por Sectores e intervalos , Graficas '2D' # Girni 2020-10-07 propuesta: edelros@espol.edu.ec import numpy as np import pandas as pd import json import matplotlib.pyplot as plt import girni_lora_libreria as girni # INGRESO # archivos de entrada modo = 'rx' medida = 'rssi' arch_medidaubica = 'rsmP06_'+medida+'Ubica01sector1.txt' # archivos de salida arch_ecuaciones = 'rsmP07_ecuacionSector01.json' arch_medUbAtrib = 'rsmP07_'+medida+'UbicaUsarSector01.txt' # Analizar por segmentos analiza = {'gtwRECT':{'analizar' : 1, 'sector_ref' : ['FIEC112','FCNM110'], 's0':{'atipico_std' : 1, 'frontera' : [300], 'atipInterv_std': [2,2], 'p_amplia': 2, 'grp' : ['RECT','FIEC'], 'tip' : ['punto'], 'LOS' : [1] }, 's1':{'atipico_std' : 1, 'frontera' : [], 'atipInterv_std': [2], 'p_amplia': 2, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [1,0] } }, 'gtwFIEC':{'analizar' : 1, 'sector_ref' : [], 's0':{'atipico_std' : 1, 'frontera' : [190], 'atipInterv_std': [1,1], 'p_amplia': 4, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [0,1] } }, 'gtwFCNM':{'analizar' : 1, 'sector_ref' : [], 's0':{'atipico_std' : 1, 'frontera' : [235.0], 'atipInterv_std': [2,2], 'p_amplia': 4, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [1,0] } } } baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} # Parámetros de grafica tipograf = '2D' # '2D','' sin grafica escala = 'log' # 'normal','log' escalabase = 10 # 10 casicero = 1e-4 precision = 2 intersectar = 1 # 0:Falso, 1: Verdadero # PROCEDIMIENTO # leer datos tabla = pd.read_csv(arch_medidaubica, index_col='etiqueta') tabla = pd.DataFrame(tabla) baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) # Resultados de análisis ecuacion = {} eq_graf = {} # analiza datos hacia una baliza for unabaliza in analiza: donde = baliza_val.index(unabaliza) cualbaliza = baliza_key[donde] # Parámetros analizar = analiza[unabaliza]['analizar'] if analizar: # Crea ecuacion por baliza ecuacion[unabaliza] = {'sector_rad':[]} eq_graf[unabaliza] = {} # sectores sectores = [] sector_ref = analiza[unabaliza]['sector_ref'] tabla['sector_'+cualbaliza] = 0 # 'todos' predeterminado # coordenadas baliza para identificar ángulo b_este = tabla['c_este'][unabaliza] b_norte = tabla['c_norte'][unabaliza] # sectores por puntos de referencia if len(sector_ref)>0: for cadapunto in sector_ref: p_este = tabla['c_este'][cadapunto] p_norte = tabla['c_norte'][cadapunto] dx = p_este - b_este dy = p_norte - b_norte theta = np.arctan2(dy,dx) if theta<0 and dx<0: theta = theta + 2*np.pi sectores.append(theta) sectores = np.array(sectores) ordenar = np.argsort(sectores) sectores = list(sectores[ordenar]) nsectores = len(sectores) # clasifica puntos por sector particular for cadapunto in tabla.index: dentrosector = 0 p_este = tabla['c_este'][cadapunto] p_norte = tabla['c_norte'][cadapunto] dx = p_este-b_este dy = p_norte-b_norte theta = np.arctan2(dy,dx) if theta<0 and dx<0: theta = theta + 2*np.pi for j in range(0,nsectores-1,1): if theta>sectores[j] and theta<sectores[j+1]: dentrosector = j+1 tabla.loc[cadapunto,'sector_'+cualbaliza] = dentrosector # ecuacion por baliza y sector ecuacion[unabaliza]['sector_rad'] = sectores nsectores = len(sectores) if nsectores == 0: nsectores = 1 for cadasector in range(0,nsectores,1): unsector = 's'+str(cadasector) ecuacion[unabaliza][unsector] = {} eq_graf[unabaliza][unsector] = {} # ecuación con todos los puntos como referencia [pares,par_etiqueta] = girni.pares_usar(tabla,baliza,analiza, unabaliza,unsector, medida,modo) xi = pares[:,0] yi = pares[:,1] n_xi = len(xi) # coeficiente de correlación correlacion = np.corrcoef(xi,yi)[0,1] # minimos cuadrados ecuacion0 = girni.linealiza_lstsq(xi,yi) # selecciona atipicos de todos los puntos atipico_std = analiza[unabaliza][unsector]['atipico_std'] alpha = ecuacion0['alpha'] beta = ecuacion0['beta'] fdist0 = lambda d: -10*alpha*(np.log10(d))+beta yi0 = fdist0(xi) dyi0std = ecuacion0['error_std'] dyi0 = yi - yi0 atipicos = np.abs(dyi0) >= dyi0std*atipico_std xi0_e = xi[atipicos] yi0_e = yi[atipicos] etiq0_e = par_etiqueta[atipicos] unintervalo = 'r0' # todos # para exportar hacia archivo o gráfica ecuacion[unabaliza][unsector] = {unintervalo: ecuacion0 } ecuacion[unabaliza][unsector][unintervalo]['correlacion'] = correlacion eq_graf[unabaliza][unsector] = {unintervalo: {'xi_graf' : xi, 'yi_graf' : yi, 'etiqueta' : par_etiqueta, 'linea' : yi0, 'atipicos' : [xi0_e,yi0_e], 'atip_etiq': etiq0_e} } # Intervalos radiales en sector intervalo = [np.min(xi),np.max(xi)] frontera = analiza[unabaliza][unsector]['frontera'] if len(frontera)>0: # revisar si frontera esta dentro intervalo frontera = np.array(frontera, dtype=float) revisar = (frontera>=np.min(xi)) & (frontera<=np.max(xi)) enintervalo = list(frontera[revisar]) intervalo.extend(enintervalo) intervalo = np.array(intervalo) ordenar = np.argsort(intervalo) intervalo = intervalo[ordenar] n_intervalo = len(intervalo) # analizar cada subintervalo p_inicio = 0 p_desde = 0 p_amplia = analiza[unabaliza][unsector]['p_amplia'] atipIntv_std = analiza[unabaliza][unsector]['atipInterv_std'] for i in range(0,n_intervalo-1,1): i_eq = 'r' + str(i+1) # puntos en subintervalo [a,b] a = intervalo[i] b = intervalo[i+1] subintervalo = (xi >= a) & (xi <= b) xi_sub = xi[subintervalo] yi_sub = yi[subintervalo] n_sub = len(xi_sub) etiq_sub = par_etiqueta[p_inicio:p_inicio + n_sub] # amplia sub-intervalo, mejora intersecta rectas detras = p_inicio retrocede = detras if detras > p_amplia: retrocede = p_amplia delante = n_xi - (p_inicio+n_sub)# -1) avanza = delante if delante >= p_amplia: avanza = p_amplia p_desde = p_inicio - retrocede p_hasta = p_inicio + (n_sub) + avanza p_inicio = p_inicio + (n_sub-1) # subintervalo, amplia puntos xi_a = xi[p_desde:p_hasta] yi_a = yi[p_desde:p_hasta] etiq_a = par_etiqueta[p_desde:p_hasta] # coeficiente de correlación correlacion1 = np.corrcoef(xi_a,yi_a)[0,1] # analiza subintervalo ecuacion1 = girni.linealiza_lstsq(xi_a,yi_a) ecuacion[unabaliza][unsector][i_eq] = ecuacion1 ecuacion[unabaliza][unsector][i_eq]['correlacion'] = correlacion1 # atipicos del subintervalo extendido alpha = ecuacion1['alpha'] beta = ecuacion1['beta'] fdist1 = lambda d: -10*alpha*(np.log10(d))+beta yi1 = fdist1(xi_a) dyi1std = ecuacion1['error_std'] atipicos = np.zeros(len(xi_a),dtype=bool) atipico_std = analiza[unabaliza][unsector]['atipInterv_std'][i] dyi1 = yi_a - yi1 if np.abs(dyi1std) > casicero: atipicos = np.abs(dyi1) >= dyi1std*atipico_std xi1_e = xi_a[atipicos] yi1_e = yi_a[atipicos] etiq1_e = etiq_a[atipicos] # para gráfica, atipicos sin extender puntos atipicos_sub = (xi1_e >= a) & (xi1_e<=b) xi_sub1_e = xi1_e[atipicos_sub] yi_sub1_e = yi1_e[atipicos_sub] etiq_sub1e = etiq1_e[atipicos_sub] eq_graf[unabaliza][unsector][i_eq] = {'atipicos': [xi_sub1_e,yi_sub1_e], 'atip_etiq':etiq_sub1e} # subintervalo sin atipicos if len(xi1_e)>0: atipicoNo = np.abs(dyi1) <= dyi1std*atipico_std xi2 = xi_a[atipicoNo] yi2 = yi_a[atipicoNo] etiq2 = etiq_a[atipicoNo] # coeficiente de correlación correlacion2 = np.corrcoef(xi2,yi2)[0,1] ecuacion2 = girni.linealiza_lstsq(xi2,yi2) # actualiza ecuación sin atipicos intervaloy intervalox = ecuacion1['intervalox'] ecuacion2['intervalox'] = intervalox.copy() alpha = ecuacion2['alpha'] beta = ecuacion2['beta'] fdist = lambda d: -10*alpha*(np.log10(d))+beta intervaloy = fdist(intervalox) ordenar = np.argsort(intervaloy) intervaloy = list(intervaloy[ordenar]) ecuacion2['intervaloy'] = intervaloy ecuacion[unabaliza][unsector][i_eq] = ecuacion2 ecuacion[unabaliza][unsector][i_eq]['correlacion'] = correlacion2 # Revisar frontera entre subintervalos, # calcula intersección de rectas como nueva frontera interv_calc = np.copy(intervalo) if len(intervalo) >2 and intersectar==1 : for i in range(0,n_intervalo-2,1): ai = 'r' + str(i+1) bi = 'r' + str(i+2) ma = ecuacion[unabaliza][unsector][ai]['alpha'] ba = ecuacion[unabaliza][unsector][ai]['beta'] mb = ecuacion[unabaliza][unsector][bi]['alpha'] bb = ecuacion[unabaliza][unsector][bi]['beta'] # punto de intersección o cruce cruzanx = 10**((bb-ba)/(10*(mb-ma))) dfrontera = frontera - cruzanx # cruce dentro de intervalo de ecuacion if cruzanx > intervalo[-1]: cruzanx = intervalo[-1] if cruzanx < intervalo[0]: cruzanx = intervalo[0] interv_calc[i+1] = cruzanx # para grafica evalua cada subintervalo sin atipicos n_interv_calc = len(interv_calc) for i in range(0,n_interv_calc-1,1): i_eq = 'r'+str(i+1) a = interv_calc[i] b = interv_calc[i+1] subintervalo = (xi >= a) & (xi <= b) xi_sub = xi[subintervalo] yi_sub = yi[subintervalo] xi_graf = np.copy(xi[subintervalo]) if not(a in xi_graf): xi_graf = np.concatenate(([a],xi_graf),axis=0) if not(b in xi_graf): xi_graf = np.concatenate((xi_graf,[b]),axis=0) # Evalua subintervalo con la ecuacion sin atipicos alpha = ecuacion[unabaliza][unsector][i_eq]['alpha'] beta = ecuacion[unabaliza][unsector][i_eq]['beta'] fdist = lambda d: -10*alpha*(np.log10(d))+beta yi1_sub = fdist(xi_sub) yi_graf = fdist(xi_graf) eq_graf[unabaliza][unsector][i_eq]['xi_graf'] = xi_graf eq_graf[unabaliza][unsector][i_eq]['yi_graf'] = yi_graf a = np.round(np.min([xi_graf]),precision) b = np.round(np.max([xi_graf]),precision) ecuacion[unabaliza][unsector][i_eq]['intervalox'] = [a,b] ay = np.round(np.min([yi_graf]),precision) by = np.round(np.max([yi_graf]),precision) ecuacion[unabaliza][unsector][i_eq]['intervaloy'] = [ay,by] # SALIDA for unabaliza in ecuacion: for unsector in ecuacion[unabaliza]: if unsector == 'sector_rad': print('baliza: ',unabaliza) print(' sectores radianes: ',ecuacion[unabaliza]['sector_rad']) if unsector != 'sector_rad': for i_eq in ecuacion[unabaliza][unsector]: unintervalo = ecuacion[unabaliza][unsector][i_eq]['intervalox'] unintervaloy = ecuacion[unabaliza][unsector][i_eq]['intervaloy'] error_medio = ecuacion[unabaliza][unsector][i_eq]['error_medio'] error_std = ecuacion[unabaliza][unsector][i_eq]['error_std'] eq_latex = ecuacion[unabaliza][unsector][i_eq]['eq_latex'] errorx_medio = ecuacion[unabaliza][unsector][i_eq]['errorx_medio'] errorx_std = ecuacion[unabaliza][unsector][i_eq]['errorx_std'] correlacion = ecuacion[unabaliza][unsector][i_eq]['correlacion'] print(' [sector][intervalo]: ',unsector,',',i_eq) print(' ' + eq_latex) print(' ','intervalox: ',np.round(unintervalo,precision)) print(' ','intervaloy: ',np.round(unintervaloy,precision)) print(' correlación: ',np.round(correlacion,precision)) print(' |error_rssi| promedio: ',np.round(error_medio,precision), ' , std:',np.round(error_std,precision)) print(' |error_dist| promedio: ',np.round(errorx_medio,precision), ' , std:',np.round(errorx_std,precision)) print() # salida hacia archivo with open(arch_ecuaciones, 'w') as outfile: json.dump(ecuacion, outfile) tabla.to_csv(arch_medUbAtrib) # GRAFICA # Referencias para gráfica grupo = ['FIEC' ,'FCNM' ,'RECT','CIRC'] colores = ['green','orange','grey','magenta'] tipo = ['punto','1m' ,'gtw','dispositivo'] marcas = [ 'o','D' ,'D' ,'*' ] if tipograf=='2D': for unabaliza in ecuacion: for unsector in ecuacion[unabaliza]: if not(unsector=='sector_rad'): figura,grafica = plt.subplots() if escala == 'log': grafica.set_xscale(escala,base=escalabase) # todos los puntos unintervalo = 'r0' xi = eq_graf[unabaliza][unsector][unintervalo]['xi_graf'] yi = eq_graf[unabaliza][unsector][unintervalo]['yi_graf'] etiqueta = eq_graf[unabaliza][unsector][unintervalo]['etiqueta'] grafica.scatter(xi,yi,marker='.') m = len(xi) for i in range(0,m,1): grafica.annotate(etiqueta[i],(xi[i],yi[i])) # linealizado con todos los puntos fdtxt = ecuacion[unabaliza][unsector][unintervalo]['eq_latex'] yi0 = eq_graf[unabaliza][unsector][unintervalo]['linea'] a = np.round(np.min([xi]),precision) b = np.round(np.max([xi]),precision) eq_texto = fdtxt +' ; ['+ str(a) +','+ str(b)+']' grafica.plot(xi,yi0,label=eq_texto,linestyle='dotted') # linealizado por subintervalo eq_interv = list(ecuacion[unabaliza][unsector].keys()) eq_interv.pop(0) n_intervalo = len(eq_interv) for i_eq in eq_interv: fdtxt = ecuacion[unabaliza][unsector][i_eq]['eq_latex'] grtxt = ecuacion[unabaliza][unsector][i_eq]['eqg_latex'] xi_graf = eq_graf[unabaliza][unsector][i_eq]['xi_graf'] yi_graf = eq_graf[unabaliza][unsector][i_eq]['yi_graf'] a = np.round(np.min([xi_graf]),precision) b = np.round(np.max([xi_graf]),precision) eq_texto = fdtxt+' ; ['+str(a)+','+str(b)+']' grafica.plot(xi_graf,yi_graf, label=eq_texto) # atipicos marcados en subintervalo [xi1_e,yi1_e] = eq_graf[unabaliza][unsector][i_eq]['atipicos'] etiq1_e = eq_graf[unabaliza][unsector][i_eq]['atip_etiq'] grafica.scatter(xi1_e,yi1_e, color='red') m = len(etiq1_e) for i in range(0,m,1): grafica.annotate(etiq1_e[i], (xi1_e[i],yi1_e[i]), color='red') # lineas de frontera grafica.axvline(a, color='lightblue') valor_frontera = str(np.round(a,precision)) grafica.annotate(valor_frontera, (a,np.max([yi,yi0])), color='lightblue') grafica.axvline(b, color='lightblue') valor_frontera = str(np.round(b,precision)) grafica.annotate(valor_frontera, (b,np.max([yi,yi0])), color='lightblue') # etiquetas y títulos grafica.legend() grafica.set_ylabel(medida+'_'+modo) grafica.set_xlabel('distancia') grafica.grid(True,linestyle='dotted', axis='x', which='both') untitulo = unabaliza+'_'+unsector+': ' untitulo = untitulo+medida+'_'+modo+' vs distancia' grafica.set_title(untitulo) plt.show()
Para la baliza de Rectorado, hacia el área de estudio se encuentra el edificio Biblioteca que es suficientemente grande para bloquear parcialmente la señal y genera un efecto "sombra".

En la vista superior del área de mediciones, a la derecha se ubica el rectorado en la cima del cerro, la Biblioteca en una parte intermedia, y el área de vegetacion FIEC se ubica en la parte baja del cerro hacia la izquierda de la imagen.
La "sombra" en la parte de vegetación se delimita en el sector formado por el ángulo formado entre las líneas de baliza y punto de referencia.
En la imagen se identifica como sector 's0' al círculo completo, como si no hubiese sectorización, para luego realizar cortes para el sector 's1' de la "sombra".
El sector 's1', del ejemplo, usa los puntos de referencia de inicio y fin en el sentido de las manecillas del reloj:
- 'FIEC112' usado como inicio, pues la línea entre Rectorado y el punto FIEC112 pasa por el borde del edificio de Biblioteca.
- 'FCNM110' es usado punto final del sector al delimitar el área de vegetación bajo estudio entre FIEC y FCNM desde RECTorado.
En cada sector, se usan también intervalos por distancia desde la baliza descrita en la sección anterior.
El asunto con sectores se presenta principalmente con la baliza 'gtwRECT', siendo el caso referencia para el desarrollo del algoritmo. El sector añade una variable y nivel al diccionario de la ecuación.
Para el primer sector 's0' sin "somlbra" del edificion biblioteca, también se aplica un subintervalo con frontera buscada desde los 300 m y determinada con las fórmulas en un radio de 359 m.
Para el siguiente sector 's1' se observa el efecto de "sombra" del edificio Biblioteca, se presenta una recuperación de señal al alejar de la baliza de RECTorado y el edificio Biblioteca.
En la gráfica, la baliza de RECTorado se encuentra a la izquierda, pues el eje distancia aumenta de valor hacia la derecha.
La variable 'sector_ref' contiene los puntos de referencia para un nuevo sector 's1'. Si 'sector_ref' no contiene valores [] se asume que una formula aplica todo el círculo predeterminada como sector 's0'.
Los puntos de referencia se convierten a su equivalente en radianes usando las coordenadas utm este y norte, valores en radianes que pasan a formar parte de diccionario de ecuaciones como 'sector_rad' usados luego para evaluar la ecuación.
# Analizar por segmentos analiza = {'gtwRECT':{'analizar' : 1, 'sector_ref' : ['FIEC112','FCNM110'], 's0':{'atipico_std' : 1, 'frontera' : [300], 'atipInterv_std': [2,2], 'p_amplia': 2, 'grp' : ['RECT','FIEC'], 'tip' : ['punto'], 'LOS' : [1] }, 's1':{'atipico_std' : 1, 'frontera' : [], 'atipInterv_std': [2], 'p_amplia': 2, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [1,0] } }, 'gtwFIEC':{'analizar' : 1, 'sector_ref' : [], 's0':{'atipico_std' : 1, 'frontera' : [190], 'atipInterv_std': [1,1], 'p_amplia': 4, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [0,1] } }, 'gtwFCNM':{'analizar' : 1, 'sector_ref' : [], 's0':{'atipico_std' : 1, 'frontera' : [235.0], 'atipInterv_std': [2,2], 'p_amplia': 4, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [1,0] } } }
El caso de la baliza 'gtwFIEC' no tiene observaciones de "sombra" para el área de vegetación que sean de tamaño considerable, por lo que se mantiene solo la división por segmentos.
Los resultados no varían gtwFCNM, pues no se ha aplicado este concepto de "sombra" para estas balizas, tan solo la división por subintevalos causadas por cambios de entorno.
Los resultados del algoritmo para usar en localización :
baliza: gtwRECT
sectores radianes: [2.6552133371486635, 2.7999991438538827]
[sector][intervalo]: s0 , r0
$ rssi = -10(5.148)log_{10}(d)+(15.043) $
intervalox: [138.15 482.74]
intervaloy: [-123.1 -93.18]
correlación: -0.93
|error_rssi| promedio: 2.88 , std: 3.55
|error_dist| promedio: 39.64 , std: 44.91
[sector][intervalo]: s0 , r1
$ rssi = -10(5.001)log_{10}(d)+(11.842) $
intervalox: [138.15 359.35]
intervaloy: [-115.97 -95.2 ]
correlación: -0.9
|error_rssi| promedio: 4.18 , std: 4.75
|error_dist| promedio: 42.76 , std: 44.83
[sector][intervalo]: s0 , r2
$ rssi = -10(7.191)log_{10}(d)+(67.794) $
intervalox: [359.35 482.74]
intervaloy: [-125.18 -115.97]
correlación: -0.94
|error_rssi| promedio: 2.11 , std: 2.3
|error_dist| promedio: 25.23 , std: 28.25
[sector][intervalo]: s1 , r0
$ rssi = -10(-8.383)log_{10}(d)+(-337.543) $
intervalox: [374.66 443.48]
intervaloy: [-124.2 -113.71]
correlación: 0.66
|error_rssi| promedio: 1.79 , std: 2.2
|error_dist| promedio: 20.48 , std: 25.57
[sector][intervalo]: s1 , r1
$ rssi = -10(-8.383)log_{10}(d)+(-337.543) $
intervalox: [374.66 443.48]
intervaloy: [-121.79 -115.65]
correlación: 0.66
|error_rssi| promedio: 1.79 , std: 2.2
|error_dist| promedio: 20.48 , std: 25.57
baliza: gtwFIEC
sectores radianes: []
[sector][intervalo]: s0 , r0
$ rssi = -10(4.908)log_{10}(d)+(1.406) $
intervalox: [ 52.54 397.15]
intervaloy: [-129.13 -86.99]
correlación: -0.9
|error_rssi| promedio: 4.84 , std: 5.56
|error_dist| promedio: 41.43 , std: 54.09
[sector][intervalo]: s0 , r1
$ rssi = -10(4.263)log_{10}(d)+(-11.269) $
intervalox: [ 52.54 166.14]
intervaloy: [-105.93 -84.62]
correlación: -0.9
|error_rssi| promedio: 2.92 , std: 3.33
|error_dist| promedio: 20.19 , std: 24.67
[sector][intervalo]: s0 , r2
$ rssi = -10(6.09)log_{10}(d)+(29.295) $
intervalox: [166.14 397.15]
intervaloy: [-128.98 -105.93]
correlación: -0.92
|error_rssi| promedio: 2.71 , std: 3.17
|error_dist| promedio: 25.03 , std: 29.93
baliza: gtwFCNM
sectores radianes: []
[sector][intervalo]: s0 , r0
$ rssi = -10(5.403)log_{10}(d)+(8.423) $
intervalox: [ 27.74 364.71]
intervaloy: [-132.09 -81.62]
correlación: -0.93
|error_rssi| promedio: 4.59 , std: 5.48
|error_dist| promedio: 41.33 , std: 48.24
[sector][intervalo]: s0 , r1
$ rssi = -10(4.795)log_{10}(d)+(-3.65) $
intervalox: [ 27.74 238.81]
intervaloy: [-117.68 -72.85]
correlación: -0.91
|error_rssi| promedio: 5.96 , std: 6.51
|error_dist| promedio: 52.15 , std: 64.38
[sector][intervalo]: s0 , r2
$ rssi = -10(9.027)log_{10}(d)+(96.989) $
intervalox: [238.81 364.71]
intervaloy: [-134.28 -117.68]
correlación: -0.87
|error_rssi| promedio: 2.81 , std: 3.43
|error_dist| promedio: 20.26 , std: 25.06
>>>
# Localización por trilateración # Ubicación de puntos en el mapa # Girni 2020-10-07 propuesta: edelros@espol.edu.ec import numpy as np import sympy as sym import matplotlib.pyplot as plt import pandas as pd import json import girni_lora_libreria as girni # INGRESO # revisar parametros al inicio modo = 'rx' medida = 'rssi' # archivos de entrada arch_medUbAtrib = 'rsmP06_'+medida+'UbicaUsar01.txt' arch_ecuaciones = 'rsmP06_ecuaciones01.json' # archivos de salida arch_trilatera = 'rsmP07_'+medida+'trilatera01.txt' # grupo a procesar mostrargrp = ['FIEC'] #['FIEC','FCNM','RECT','CIRC'] mostrartip = ['punto'] mostrarfuera = [0,1] #[0,1] tolera_error = 2 # decimales en error # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} # PROCEDIMIENTO baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) # leer datos with open(arch_ecuaciones) as json_file: ecuacion = json.load(json_file) tabla = pd.read_csv(arch_medUbAtrib, index_col='etiqueta') tabla = pd.DataFrame(tabla) # coordenadas de baliza coordbaliza = {} for cadabaliza in baliza: cualbaliza = baliza[cadabaliza] coordbaliza[cadabaliza] = [tabla['c_este'][cualbaliza]] coordbaliza[cadabaliza].append(tabla['c_norte'][cualbaliza]) # inicializa ubicados, encontrados, intervalos fuera, errores # ubicados tiene [distancia, distancia+1s, distancia +2s,total] ubicados = np.zeros(shape=(3,4),dtype=int) tabla['interv_fuera'] = '' tabla['encontrado'] = np.nan # suma de errores sumatrilat = np.zeros(shape=(2,4),dtype=float) sumagps = np.zeros(shape=(2,4),dtype=float) sumagpsdx = np.zeros(shape=(2,4),dtype=float) sumagpsdy = np.zeros(shape=(2,4),dtype=float) # distancias y errores a cada baliza for unabaliza in baliza_val: donde = baliza_val.index(unabaliza) cualbaliza = baliza_key[donde] columna = medida+'_'+modo+'_'+cualbaliza tabla['dist0_'+cualbaliza] = np.nan tabla['dist1_'+cualbaliza] = np.nan tabla['dist2_'+cualbaliza] = np.nan # distancia estimada por punto for cadapunto in tabla.index: p_rssi = tabla[columna][cadapunto] esgrupo = tabla['grupo'][cadapunto] estipo = tabla['tipo'][cadapunto] # ecuacion a usar ecuacion_rssi = ecuacion[unabaliza] if not(np.isnan(p_rssi)): if (esgrupo in mostrargrp) and (estipo in mostrartip): ubicados[2,donde] = ubicados[2,donde] + 1 dist = girni.dist_rssi(p_rssi,ecuacion_rssi) [distancia,e_mean,e_1std,e_2std,interv_fuera] = dist dist1 = distancia + e_1std dist2 = distancia + e_2std tabla.loc[cadapunto,'dist0_'+cualbaliza] = distancia tabla.loc[cadapunto,'dist1_'+cualbaliza] = dist1 tabla.loc[cadapunto,'dist2_'+cualbaliza] = dist2 if interv_fuera>0: if len(tabla['interv_fuera'][cadapunto])==0: separador='' else: separador=',' tabla.loc[cadapunto,'interv_fuera'] = tabla['interv_fuera'][cadapunto]+separador+cualbaliza procesados = np.max(ubicados[2,:]) # trilateración. estima localización cada punto # inicializa cada punto a i*std for i in range(0,3,1): tabla['trilat_este_'+str(i)] = np.nan tabla['trilat_norte_'+str(i)] = np.nan tabla['trilat_error_'+str(i)] = np.nan tabla['ubicado_'+str(i)] = np.nan tabla['trilat_gps_error_'+str(i)] = np.nan tabla['trilat_gps_dx_'+str(i)] = np.nan tabla['trilat_gps_dy_'+str(i)] = np.nan # procesa cada punto for cadapunto in tabla.index: esgrupo = tabla['grupo'][cadapunto] if esgrupo in mostrargrp: # coordenadas GPS del punto c_este = tabla['c_este'][cadapunto] c_norte = tabla['c_norte'][cadapunto] # cada punto a i*std punto = {} for i in range(0,3,1): punto[i] = {} cuenta = 0 for unabaliza in baliza: punto[i][unabaliza] = tabla['dist'+str(i)+'_'+unabaliza][cadapunto] # si existe distancia if not(np.isnan(punto[i][unabaliza])): cuenta = cuenta + 1 # Hay 3 mediciones a baliza if cuenta==3: localiza = girni.trilatera(punto[i], coordbaliza, tolera = 10e-4) baricentro = localiza['baricentro'] barerror = localiza['barerror'] poligono = localiza['poligono'] sumabaricentro = np.sum(baricentro) # Hay coordenadas de baricentro if not(np.isnan(sumabaricentro)): tabla.loc[cadapunto,'trilat_este_'+str(i)] = baricentro[0] tabla.loc[cadapunto,'trilat_norte_'+str(i)] = baricentro[1] tabla.loc[cadapunto,'trilat_error_'+str(i)] = np.round(barerror,tolera_error) # error trilatera hacia gps dx = baricentro[0] - c_este dy = baricentro[1] - c_norte error_gps = np.sqrt(dx**2+dy**2) tabla.loc[cadapunto,'trilat_gps_error_'+str(i)] = np.round(error_gps,tolera_error) tabla.loc[cadapunto,'trilat_gps_dx_'+str(i)] = np.round(dx,tolera_error) tabla.loc[cadapunto,'trilat_gps_dy_'+str(i)] = np.round(dy,tolera_error) # cuenta error si encuentra primera vez cond1 = np.isnan(tabla['encontrado'][cadapunto]) cond2 = len(tabla['interv_fuera'][cadapunto])>0 k = int(cond2) # intervalo extendido if cond1: tabla.loc[cadapunto,'encontrado'] = i ubicados[k,i] = ubicados[k,i]+1 sumatrilat[k,i] = sumatrilat[k,i] + np.round(barerror,tolera_error) sumagps[k,i] = sumagps[k,i] + np.round(error_gps,tolera_error) sumagpsdx[k,i] = sumagpsdx[k,i] + np.round(np.abs(dx),tolera_error) sumagpsdy[k,i] = sumagpsdy[k,i] + np.round(np.abs(dy),tolera_error) # contabiliza errores de localizados ubicasuma = np.zeros(2) ubicasumporc = np.zeros(2) ubicaporc = np.zeros(shape=(2,3)) for k in range(0,2,1): ubicados[k,3] = int(np.sum(ubicados[k,0:3])) ubicasuma[k] = np.sum(ubicados[k,0:3]) ubicasumporc[k] = np.round(100*ubicasuma[k]/ubicados[k,3],1) for i in range(0,3,1): ubicaporc[k,i] = np.round(100*ubicados[k,i]/ubicasuma[k],1) if ubicados[k,i]>0: sumatrilat[k,i] = np.round(sumatrilat[k,i]/ubicados[k,i],1) sumagps[k,i] = np.round(sumagps[k,i]/ubicados[k,i],1) sumagpsdx[k,i] = np.round(sumagpsdx[k,i]/ubicados[k,i],1) sumagpsdy[k,i] = np.round(sumagpsdy[k,i]/ubicados[k,i],1) # SALIDA print('Errores localizacion') import prettytable as ptt print('Errores estimado: Cota-Trilatera-polígono y Trilatera_vs_GPS') mostrar = ptt.PrettyTable(['punto','i*std','fuera','trilat', 'gps','gps_dx','gps_dy', 'u_d1','u_d2','u_d3']) for cadapunto in tabla.index: # selecciona puntos a mostrar encontrado = tabla['encontrado'][cadapunto] esgrupo = tabla['grupo'][cadapunto] interv_fuera = int(len(tabla['interv_fuera'][cadapunto])!=0) cond1 = not(np.isnan(encontrado)) cond2 = esgrupo in mostrargrp cond3 = interv_fuera in mostrarfuera if cond1 and cond2 and cond3: encontrado = int(encontrado) mostrar.add_row([cadapunto, str(int(tabla['encontrado'][cadapunto])), tabla['interv_fuera'][cadapunto], str(tabla['trilat_error_'+str(encontrado)][cadapunto]), str(tabla['trilat_gps_error_'+str(encontrado)][cadapunto]), str(tabla['trilat_gps_dx_'+str(encontrado)][cadapunto]), str(tabla['trilat_gps_dy_'+str(encontrado)][cadapunto]), tabla['usar_d1'][cadapunto], tabla['usar_d2'][cadapunto], tabla['usar_d3'][cadapunto]]) print(mostrar) print('puntos con medidas: ',procesados) loc_alg = np.round(100*np.sum(ubicados[:,3])/procesados,1) print('localizados con algoritmo: ', np.sum(ubicados[:,3]), ' , '+str(loc_alg)+'%' ) print('Errores Promedio:') resumen = ptt.PrettyTable(['error+i*std','cant','%', 'trilat','gps','gps_dx', 'gps_dy']) for k in range(0,2,1): if k == 0: texto = 'dentro' if k == 1: texto = 'fuera' resumen.add_row(['interv_'+texto,ubicados[k,3],'', '','','','']) for i in range(0,3,1): resumen.add_row(['error_'+str(i),ubicados[k,i], str(ubicaporc[k,i])+'%', sumatrilat[k,i],sumagps[k,i], sumagpsdx[k,i],sumagpsdy[k,i], ]) print(resumen) # salida hacia archivo tabla.to_csv(arch_trilatera) # Grafica ubicados ------------ # Referencias para gráfica grupo = ['FIEC' ,'FCNM' ,'RECT','CIRC'] colores = ['green','orange','grey','magenta'] tipo = ['punto','1m' ,'gtw','dispositivo'] marcas = [ 'o','D' ,'D' ,'*' ] colorstd = ['lightblue', 'lightgreen','orange'] colorlin = ['lightblue', 'lightgreen','orange'] figura,grafica = plt.subplots() # balizas for unabaliza in coordbaliza: g_este = coordbaliza[unabaliza][0] g_norte = coordbaliza[unabaliza][1] grafica.scatter(g_este,g_norte, color = 'red', marker = 'D', label = cadapunto) grafica.annotate(unabaliza, (g_este,g_norte)) # Puntos for cadapunto in tabla.index: g_este = tabla['c_este'][cadapunto] g_norte = tabla['c_norte'][cadapunto] # selecciona puntos a mostrar encontrado = tabla['encontrado'][cadapunto] esgrupo = tabla['grupo'][cadapunto] interv_fuera = int(len(tabla['interv_fuera'][cadapunto])!=0) cond1 = not(np.isnan(encontrado)) cond2 = esgrupo in mostrargrp cond3 = interv_fuera in mostrarfuera if cond1 and cond2 and cond3: encontrado = int(encontrado) p_este = tabla['trilat_este_'+str(encontrado)][cadapunto] p_norte = tabla['trilat_norte_'+str(encontrado)][cadapunto] grafica.scatter(p_este,p_norte, color = colorstd[encontrado], label = cadapunto) grafica.plot([p_este,g_este], [p_norte,g_norte], color = colorstd[encontrado], linestyle='dotted') grafica.scatter(g_este,g_norte, color = 'blue', label = cadapunto) grafica.annotate(cadapunto,(g_este,g_norte), color='blue') grafica.set_xlabel('UTM_este') grafica.set_ylabel('UTM_norte') grafica.grid() grafica.set_title('Puntos Ubicados') plt.show()
Para el procesamiento de los datos se incorpora una función a girni_lora_libreria para realizar la linealización por mínimos cuadrados.
linealiza_lstsq(xi,yi,digitos = 3)
La función se encarga de convertir el eje x en log10(x), asi como construir las ecuaciones en la forma numérica lambda, latex y un diccionario con los parámetros de la ecuación.
Los datos de ingreso son xi y yi para cada eje, la variable dígitos establece los decimales a usar en la expresión en formato latex.
El resultado es un diccionario con los intervalos de los valores obtenidos para cada eje, la pendiente de la recta, el |error| promedio, la desviación estándar error_std, la ecuación en formato latex.
unaecuacion = {'alpha' : alpha,
'beta' : beta,
'eq_latex': fdtxt0,
'intervalox' : [np.min(xi),np.max(xi)],
'error_medio': dyi0mean,
'error_std' : dyi0std,
'eqg_latex' : grtxt0,
'intervaloy' : [np.min(yi),np.max(yi)],
'errorx_medio': dxi0mean,
'errorx_std' : dxi0std,
}
El resultado se puede escribir en un archivo en formato json. La ecuación se recupera desde el archivo con lo que se puede volver a construir la función en la lambda para evaluación numérica.
Se desarrolla principalmente usando la función numpy.linalg.lstsq.
La relación rssi vs distancia usa log10(xi), por lo que se incluye esta operación antes de aplicar mínimos cuadrados.
Obtenidos los parámetros, se da el formato de la expresión acorde al modelo básico de pérdidas en espacio libre en latex para mostrar como etiqueta en las gráficas.
RSSI(d) = -10 \alpha \log_{10} (d) + P_{0}La función se usa para cada baliza, y en varios segmentos, para observar los posibles resultados, también se incorporan los valores de errores,
def linealiza_lstsq(xi,yi,digitos = 3): ''' usa minimos cuadrados para entregar la ecuacion digitos: usados en expresion latex ''' unaecuacion = {} # Eje x en log10() xilog = np.log10(xi) n = len(xi) # mínimos cuadrados (least square), # distancia vs medida A = np.vstack([xilog, np.ones(n)]).T [m0, b0] = np.linalg.lstsq(A, yi, rcond=None)[0] alpha = -m0/10 beta = b0 # ecuaciones expresion rssi(d) fdist0 = lambda d: -10*alpha*(np.log10(d))+beta fdtxt0 = r'$ rssi = -10(' + str(np.round(alpha,digitos)) fdtxt0 = fdtxt0 + ')log_{10}(d)+(' fdtxt0 = fdtxt0 + str(np.round(beta,digitos))+') $' # Errores respecto a rssi(d) yi0 = fdist0(xi) dyi0 = yi - yi0 dyi0mean = np.mean(np.abs(dyi0)) dyi0std = np.std(dyi0, dtype=np.float64) # ecuaciones expresion d(rssi) grssi0 = lambda rssi: 10**((beta-rssi)/(10*alpha)) grtxt0 = r"$ d = 10^{(" + str(np.round(beta,digitos)) + ' - ' grtxt0 = grtxt0 + 'rssi)/' + '(10('+str(np.round(alpha,digitos))+'))} $' # Errores respecto a rssi(d) xi0 = grssi0(yi) dxi0 = xi - xi0 dxi0mean = np.mean(np.abs(dxi0)) dxi0std = np.std(dxi0, dtype=np.float64) unaecuacion = {'alpha' : alpha, 'beta' : beta, 'eq_latex': fdtxt0, 'intervalox' : [np.min(xi),np.max(xi)], 'error_medio': dyi0mean, 'error_std' : dyi0std, 'eqg_latex' : grtxt0, 'intervaloy' : [np.min(yi),np.max(yi)], 'errorx_medio': dxi0mean, 'errorx_std' : dxi0std, } return(unaecuacion)
Referencias:
Burden R, Faires J, Burden A, Análisis numérico, Décima Edición 8.1 p370.
Chapra C, Canale R. Métodos numéricos para ingenieros, Quinta edición 17.1.2 p469.
Numpy org. Least Square function. numpy.linalg.lstsq
Mínimos cuadrados. https://es.wikipedia.org/wiki/M%C3%ADnimos_cuadrados