El comportamiento de la señal de cada baliza hacia un punto en particular se observa al calcular algunos valores de estadística.
El valor principal para el modelo de localización usado es el promedio de rssi de cada baliza en el punto.
Otro valor comprementario la desviación estándar (std, σ) que es una medida de dispersión alrededor de la media. Estas variaciones estan asociadas a múltiples factores que depende de las características del entorno.

Si hay valores de promedios de un punto que son atípicos a la tendencia entre Rssi y la distancia se puede recurrir a ésta sección para observar el punto.
Con el algoritmo se obtienen los siguientes valores para el punto del ejemplo:
baliza: d1 gtwRECT muestras: 137 tramo: 17 count mean std min 25% 50% 75% max 0 118.0 -128.211864 1.960515 -132.0 -130.0 -128.5 -127.0 -123.0 baliza: d2 gtwFIEC muestras: 144 tramo: 15 count mean std min 25% 50% 75% max 0 118.0 -128.211864 1.960515 -132.0 -130.0 -128.5 -127.0 -123.0 baliza: d3 gtwFCNM muestras: 118 tramo: 9 count mean std min 25% 50% 75% max 0 118.0 -128.211864 1.960515 -132.0 -130.0 -128.5 -127.0 -123.0
Datos de ingreso
El primer valor que se requiere es el nombre del punto, ejemplo 'FIEC102', luego el modo de lectura (rx,tx') y la medida (rssi, snr).
Los datos se toman del archivo que integra en una tbala los datos del punto, en formato json del proceso anterior.
Se usa el diccionario que identifica a las balizas para realizar la tabulación de los descriptores.
# INGRESO cadapunto = 'FIEC102' modo = 'rx' medida = 'rssi' descriptor = 'mean' # Archivos de datos arch_detalles = 'rsmP02_tabla_puntosdatos01.json' # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} tolera = 1e-8
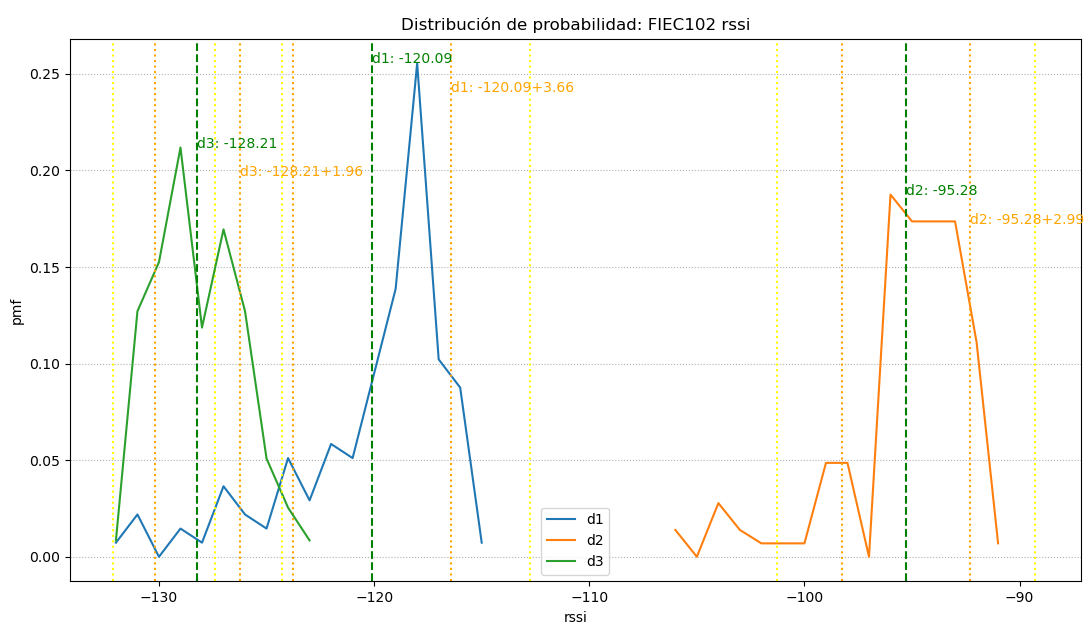
Los resultados se complementan con la gráfica que muestra la distribución de probabilidad para cada baliza, marcando también el valor de promedio y la suma de promedio mas desvición estándar.
El análisis del comportamiento de la señal de cada punto tiene relación con el entorno del punto dominado por edificios o vegetación.
Algoritmo en Python
# Revisar un punto, descriptores estadísticos # requiere un punto, modo, medida # nombre del archivo de la tabla detalle # Girni 2020-10-07 edelros@espol.edu.ec import numpy as np import pandas as pd import json import matplotlib.pyplot as plt # INGRESO cadapunto = 'FIEC102' modo = 'rx' medida = 'rssi' descriptor = 'mean' # Archivos de datos arch_detalles = 'rsmP02_tabla_puntosdatos01.json' # Referencias baliza = {'d1':'gtwRECT', 'd2':'gtwFIEC', 'd3':'gtwFCNM'} tolera = 1e-8 # PROCEDIMIENTO baliza_key = list(baliza.keys()) baliza_val = list(baliza.values()) # leer datos with open(arch_detalles) as json_file: puntodato = json.load(json_file) punto = {} for cadabaliza in baliza: punto[cadabaliza] = {} # revisa un punto unpunto = puntodato[modo][cadapunto][cadabaliza][medida+'_'+modo] unpunto = np.array(unpunto) ordenar = np.argsort(unpunto) unpunto = unpunto[ordenar] puntopd = pd.DataFrame(unpunto) describe = puntopd.describe() describe = describe.T pmin = describe['min'][0] pmax = describe['max'][0] tramo = int(pmax-pmin) conteo = np.zeros(tramo+1,dtype=int) posicion = np.arange(pmin,pmax+1,1) posicion = list(posicion) conteo = list(conteo) for valor in unpunto: donde = posicion.index(valor) conteo[donde] = conteo[donde] + 1 punto[cadabaliza] = {'muestras': len(unpunto), 'tramo': tramo, 'posicion': posicion.copy(), 'conteo': conteo.copy(), 'describe': describe} # SALIDA for cadabaliza in baliza: print('baliza:', cadabaliza, baliza[cadabaliza]) print('muestras: ', punto[cadabaliza]['muestras'], 'tramo: ' , punto[cadabaliza]['tramo']) print(describe) # grafica precision = 2 figura,grafica = plt.subplots() n_baliza = len(baliza) for cadabaliza in baliza: p_media = np.round(punto[cadabaliza]['describe']['mean'][0],precision) p_std = np.round(punto[cadabaliza]['describe']['std'][0],precision) muestras = punto[cadabaliza]['muestras'] posicion = punto[cadabaliza]['posicion'] conteo = np.array(punto[cadabaliza]['conteo'])/muestras conteomax = np.max(conteo) #grafica.plot(posicion,conteo,'o',label = cadabaliza) grafica.plot(posicion,conteo,'-',label = cadabaliza) grafica.axvline(p_media, color = 'green', linestyle = 'dashed') texto = cadabaliza + ': ' + str(p_media) grafica.annotate(cadabaliza+': '+str(p_media),(p_media,conteomax), color='green') grafica.axvline(p_media+ p_std, color ='orange', linestyle = 'dotted') texto = texto + '+' + str(p_std) grafica.annotate(texto,(p_media+p_std,conteomax-0.015), color='orange') grafica.axvline(p_media- p_std, color ='orange', linestyle = 'dotted') grafica.axvline(p_media+ 2*p_std, color ='yellow', linestyle = 'dotted') grafica.axvline(p_media- 2*p_std, color ='yellow', linestyle = 'dotted') grafica.set_xlabel('rssi') grafica.set_ylabel('pmf') texto = 'Distribución de probabilidad: '+cadapunto+' '+medida grafica.set_title(texto) grafica.grid(True,linestyle='dotted', axis='y', which='both') grafica.legend() plt.show()