Año lectivo 2024-2025 | Periodo Académico Ordinario 2
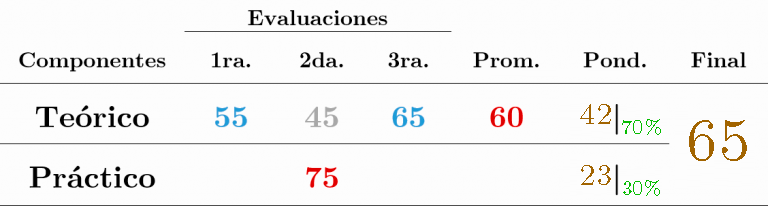
La calificación está constituida por dos componentes, uno teórico y otro práctico, con las ponderaciones que se indican a continuación.
Componente Teórico (70%)
Otras actividades: 10%
Lecciones: 40%
Evaluaciones: 50%
Los instrumentos de evaluación usados para la Evaluación del contacto con el docente (EHD) y la Evaluación del aprendizaje autónomo (EHTA), no podrán superar cada uno el 50% de la nota final sobre 100 puntos en cada parcial. La nota que se ingresa al sistema es sobre 100 y automáticamente el sistema la pondera sobre 70 puntos. (Artículo 42 – Reglamento de Grado ESPOL).
Componente Práctico (30%)
Controles de lectura:10%
Talleres formativos: 10%
Talleres sumativos: 50%
Proyecto: 30%
La Evaluación del Aprendizaje Práctico-Experimental (EHP) se evalúa a lo largo del semestre. Se ingresa al sistema al final del segundo parcial y es sobre 100 puntos, esta calificación es automáticamente ponderada a 30 puntos. La nota de la tercera evaluación puede incluir otras actividades de evaluación, excepto las que se encuentran en el componente de evaluación de horas prácticas. (Artículo 41 – Reglamento de Grado de la ESPOL)
Cabe señalar que para la primera evaluación sólo se registra en el sistema académico la nota del componente teórico. La nota del componente práctico se registra al final de la segunda evaluación en conjunto con la nota del componente teórico relacionado.
Es importante señalar que la nota de la tercera evaluación solo reemplaza (para el cómputo) la menor nota del componente teórico entre la primera y segunda evaluación; es decir, no modifica la nota del componente práctico en ningún caso.
