El algoritmo con Python se desarrolla progresivamente a partir de los ejercicios resueltos de forma analítica, usando las librerias de Sympy-Python. En caso de requerir usar el algoritmo completo, puede ir directamente al ejercicio 6 que incluye impulsos unitarios y considera el integral unilateral o completo en s.
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
..
Ejemplo 1. Transformada de Laplace de una exponencial decreciente, un solo termino
Referencia: Lathi ejemplo 4.1. p331, Oppenheim Ejemplo 9.2 p656, Hsu Ejemplo 3.1 p111 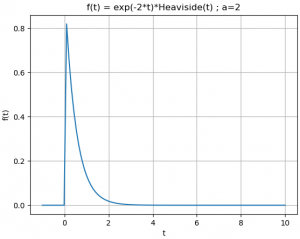
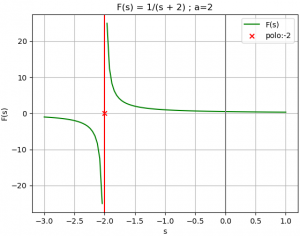
Para una señal x(t) = e-atμ(t), encuentre la transformada X(s) y su región de convergencia (ROC).
x(t) = e^{-at} μ(t)Considerando que μ(t)=0 para t<0 y μ(t)=1 para t≥0:
X(s) = \int_{0}^{\infty} e^{-at} e^{-st} \delta tSe puede observar que la región de convergencia, ROC, de X(s) es Re(s)>-a, como se muestra en la gráfica. Para otros valores de s el integral no converge.
Para el ejemplo, siendo a=2, se obtiene con el algoritmo el resultado y las gráficas presentadas.
dentro de integral f(t)*e(-st):
-t*(a + s)
e *Heaviside(t)
expresion F(s):
1
-----
a + s
{Q_polos:veces}: {-a: 1}
{P_ceros:veces}: {}
Integral de la Transformada de Laplace con Sympy-Python
Para iniciar se empieza usando una expresión simple como la del ejemplo. Semejante a los algoritmos anteriores realizados, se definen las variables tipo símbolo a usar y el escalón unitario en una expresión ‘u’ para simplificar su escritura posterior.
# INGRESO t = sym.Symbol('t', real=True) a = sym.Symbol('a', real=True) s = sym.Symbol('s') u = sym.Heaviside(t)
El desarrollo de los integrales se facilita al simplificar la expresión por términos de suma y simplificando los exponentes con la instrucción sym.powsimp().
>>> fts = ft*sym.exp(-s*t) >>> fts exp(-a*t)*exp(-s*t)*Heaviside(t) >>> fts = sym.powsimp(fts) >>> fts exp(-t*(a + s))*Heaviside(t) >>>
Las instrucciones de las operaciones para el algoritmo serán:
# PROCEDIMIENTO fts = ft*sym.exp(-s*t) # f(t,s) para integrar fts = sym.expand(fts) # expresion de sumas fts = sym.powsimp(fts) # simplifica exponentes
La integración a realizar es unilateral al considerar principalmente señales causales como se justifica en los textos, por lo que el intervalo de integración es [0,∞].
# integral Laplace unilateral
Fs_L = sym.integrate(fts,(t,0,sym.oo))
El resultado del integral se presenta por por partes o intervalos, de la forma sym.piecewise() mostrada por facilidad de lectura con sym.pprint(Fs_L).
Fs_L: / 1 pi | ----- for |arg(a + s)| < -- | a + s 2 | | oo | / < | | | -t*(a + s) | | e *Heaviside(t) dt otherwise | | |/ |0 \
La parte a usar para el desarrollo del ejercicio corresponde la primera expresión, Fs = Fs_L.args[0], que contiene expresión e intervalo. Para quedarse solo con la expresión y omitir el intervalo, se usa Fs[0]
>>> Fs = Fs_L.args[0] >>> Fs (1/(a + s), Abs(arg(a + s)) < pi/2) >>> Fs = Fs[0] >>> Fs 1/(a + s) >>>
las instrucciones para el algoritmo serán:
Fs = Fs_L.args[0] # primera ecuacion e intervalo Fs = Fs[0] # solo expresion
El comportamiento F(s), puede presentar divisiones para cero para algun valor de s llamados polos, asi como valores de s que resultan en ceros. Se usa la expresión como una fracción de polinomios P(s) y Q(s), tomando el denominador Q(s) para obtener las raíces del polinomio en Q_polos.
# polos y ceros en Fs
[P,Q] = Fs.as_numer_denom()
P = sym.poly(P,s)
Q = sym.poly(Q,s)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)
Instrucciones en Python – Ejemplo 1
# Transformada de Laplace # integral de Laplace unilateral # blog.espol.edu.ec/telg1001/ import numpy as np import matplotlib.pyplot as plt import sympy as sym # INGRESO t = sym.Symbol('t', real=True) a = sym.Symbol('a', real=True) s = sym.Symbol('s') u = sym.Heaviside(t) ft = sym.exp(-a*t)*u a_k = 2 # valor de 'a' constante # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 10 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO fts = ft*sym.exp(-s*t) # f(t,s) para integrar fts = sym.expand(fts) # expresion de sumas fts = sym.powsimp(fts) # simplifica exponentes # integral Laplace unilateral Fs_L = sym.integrate(fts,(t,0,sym.oo)) Fs = Fs_L.args[0] # primera ecuacion e intervalo Fs = Fs[0] # solo expresion # polos y ceros en Fs [P,Q] = Fs.as_numer_denom() P = sym.poly(P,s) Q = sym.poly(Q,s) P_ceros = sym.roots(P) Q_polos = sym.roots(Q) # SALIDA print(' dentro de integral f(t)*e(-st):') sym.pprint(fts) print('\n expresion F(s):') sym.pprint(Fs) print('\n {Q_polos:veces}: ',Q_polos) print(' {P_ceros:veces}: ',P_ceros)
Instrucciones para gráficar la transformada de Laplace
Se sustituye en las ecuaciones resultantes los valores de ‘a‘ con ‘a_k‘ y usando lambdify, aplicarla en en un intervalo [sa , sb] que permita mostrar una gráfica para F(s). Ejemplos de graficas se encuentran en la unidad 1.
El intervalo [sa , sb] considera los extremos de las raices o polos del denominador Q. Los polos se marcan usando puntos de dispersión con plt.scatter() y una línea vertical plt.axvline() para resaltar en la gráfica el efecto del polo.
# GRAFICA ----------- ft = ft.subs(a,a_k) # a tiene valor a_k Fs = Fs.subs(a,a_k) # f(t) # evalua en intervalo ti = np.linspace(t_a,t_b,muestras) f_t = sym.lambdify(t,ft) fti = f_t(ti) # Q polinomio denominador con valor de a # polos en s [P,Q] = Fs.as_numer_denom() Q = Q.as_poly(s) Q_polos = sym.roots(Q) # estima intervalo para s, raices reales s_a = 0 ; s_b = 0 polos = list(Q_polos.keys()) s_a = int(min(s_a,min(polos)))-1 s_b = int(max(s_b,max(polos)))+1 # F(s) # evalua en intervalo F_s = sym.lambdify(s,Fs) s_i = np.linspace(s_a,s_b,muestras) Fsi = F_s(s_i) # Revisar cuando s es complejo # grafica f(t) fig_ft, graf_ft = plt.subplots() plt.plot(ti,fti,label='f(t)') plt.xlabel('t') plt.ylabel('f(t)') plt.title('f(t) = '+str(ft)+' ; a='+str(a_k)) plt.grid() # grafica F(s) , corte en plano real fig_Fs, graf_Fs = plt.subplots() plt.plot(s_i,Fsi, color='green',label='F(s)') for raiz in Q_polos.keys(): plt.axvline(sym.re(raiz),color='red') plt.scatter(sym.re(raiz),sym.im(raiz), label='polo:'+str(raiz), marker='x',color='red') plt.axvline(0,color='gray') plt.legend() plt.xlabel('s') plt.ylabel('F(s)') plt.title('F(s) = '+str(Fs)+' ; a='+str(a_k)) plt.grid() plt.show()
Se recomienda probar con otros ejemplos desarrollados para la parte analítica y de ser necesario en cada caso mejorar el algoritmo.
Considere también que Sympy dispone de la librerías para transformadas de Laplace con instrucciones simplificadas que se usarán a lo largo de ésta unidad de estudio y que se desarrollan en la siguiente sección.
Fs_L = sym.laplace_transform(ft,t,s)
Transformada de Laplace e Inversas con Sympy-Python
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
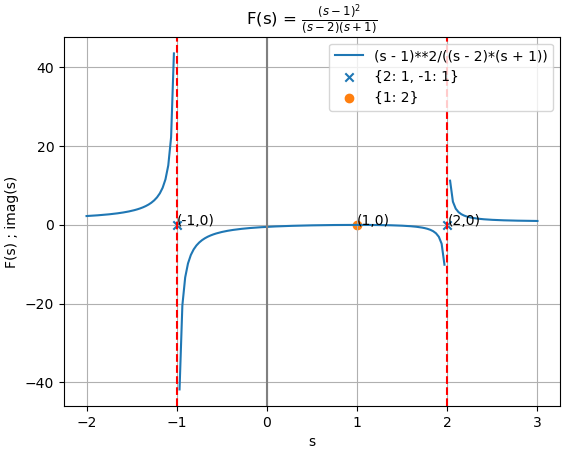
Ejemplo 2. Transformada de Laplace con suma de exponenciales
Referencia: Oppenheim Ejemplo 9.3 p658
Considere la señal que es la suma de dos exponenciales:
x(t) = 3 e^{-2t}\mu (t) - 2e^{-t}\mu (t)Del desarrollo analítico del ejercicio y usando el algoritmo se tiene que:
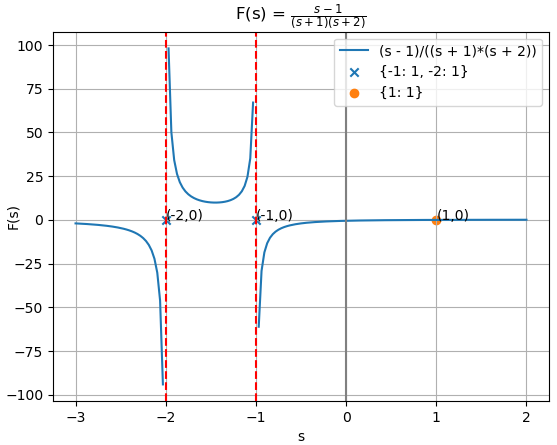
X(s) = \frac{3}{s+2}-\frac{2}{s+1}Para observar mejor los polos y ceros de X(s) se simplifica la expresión como factores en el numerador y denominador:
X(s) = \frac{s-1}{(s+2)(s+1)}La gráfica de F(s) muestra la ubicación de los polos, observando que en estos puntos la función tiende a crecer a infinito positivo o negativo,
Para el algoritmo, la función de entrada f(t) se expresa como:
u = sym.Heaviside(t) ft = 3*sym.exp(-2*t)*u - 2*sym.exp(-t)*u
Usando el algoritmo, añadiendo las partes que consideren el integral de Laplace para cada uno de los términos suma luego agrupando por factores se obtiene:
dentro de integral f(t)*e(-st):
-t*(s + 2) -t*(s + 1)
3*e *Heaviside(t) - 2*e *Heaviside(t)
expresion F(s):
s - 1
---------------
(s + 1)*(s + 2)
Q_polos{polos:veces}: {-1: 1, -2: 1}
P_ceros{polos:veces}: {1: 1}
>>>
X(s) = \frac{3}{s+2}-\frac{2}{s+1}
Considere que en la expresión X(s) no será necesario disponer de la constante ‘a‘, usada para generalizar la respuesta en el ejemplo 1. Por lo que se podría prescindir de las líneas que le hacen referencia en las instrucciones para la revisión en los polos y los títulos de las gráficas, resumidas como:
# POR COMENTAR O ELIMINAR, si no se usa constante a: # a = sym.Symbol('a', real=True) # Para graficar con s # ft = ft.subs(a,a_k) # a tiene valor a_k # Fs = Fs.subs(a,a_k) # Eliminar la 2da evaluacion de Q_polos # plt.title('f(t) = '+str(ft)) # plt.title('F(s) = '+str(Fs))
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
..
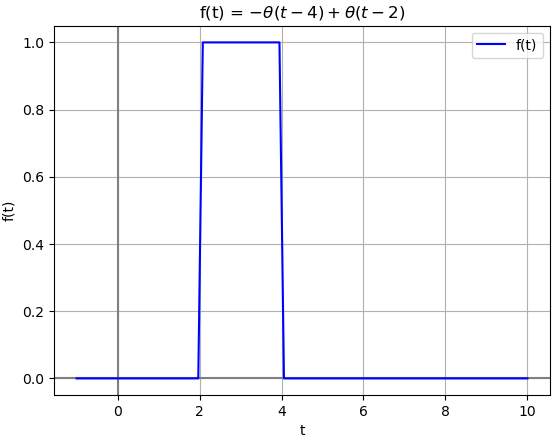
Ejemplo 3. Transformada de Laplace para suma de términos f(t) con desplazamiento, o función «gate» o compuerta
Referencia: Lathi práctica 4.1.a p337
literal a. Por integración directa, encuentra la transformada X(s) y
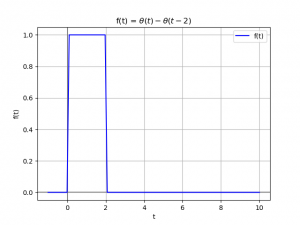 la región de convergencia para la función descrita en la imagen
la región de convergencia para la función descrita en la imagen
Analizando la expresión de la función es:
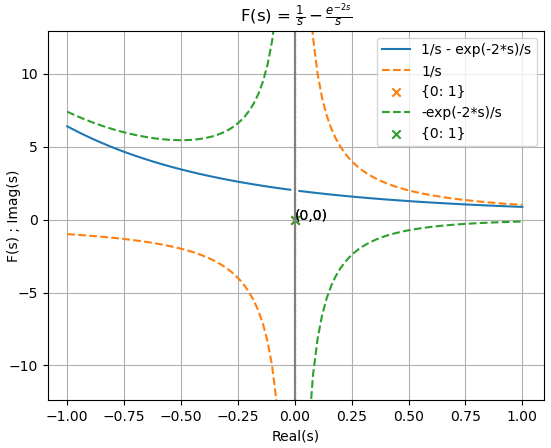
x(t) = \mu (t) - \mu (t-2)y la transformada unilateral de Laplace se expresa como:
X(s) = \frac{1}{s} - \frac{e^{-2s}}{s}La gráfica de F(s) muestra el resultado de la suma de términos o componentes. La suma de éstos términos hace que se minimice alrededor de cero el efecto creciente de cada componente.
Desarrollo con Sympy-Python
Para el caso presentado, la integral se compone de dos términos de una suma, procediendo de forma semejante al ejercicio anterior.
El bloque de ingreso se expresa como:
u = sym.Heaviside(t) ft = u - u.subs(t,t-2)
El resultado del algoritmo será:
dentro de integral f(t)*e(-st):
-s*t -s*t
e *Heaviside(t) - e *Heaviside(t - 2)
expresion F(s):
-2*s
1 e
- - -----
s s
Polos y ceros:
término: 1 * 1/s
Q_polos{polos:veces}: {0: 1}
P_ceros{polos:veces}: {}
término: exp(-2*s) * -1/s
Q_polos{polos:veces}: {0: 1}
P_ceros{polos:veces}: {}
>>>
Para el caso de polos y ceros el término con e-s no permite analizar la expresión de forma directa como un polinomio y obtener las raíces. Con la restricción descrita, el análisis se realiza agrupando los términos por cada e-s llamado componente de suma. Las veces que se repite cada polo será el mayor valor entre cada termino suma.
Instrucciones adicionales para términos con sym.exp(-a*s)
Las operaciones para obtener los polos y ceros en Sympy se realizan como polinomios sym.poly(Q,s), sin embargo ésto no considera o permite usar la expresión de F(s) con términos sym.exp(-a*s), siendo a un valor numérico.
Se obtiene una lista de todos los términos con exponencial de la forma sym.exp(-a*s), al obtener los componentes básicos de toda la expresión con Fs.atoms(sym.exp(-s)).
# separa en lista los sym.exp(-s) lista_exp = list(Fs.atoms(sym.exp(-s)))
para observar la operación se muestra el resultado de la instrucción sobre F(s)
>>> Fs
1/s - exp(-2*s)/s
>>> Fs.atoms(sym.exp(-s))
{exp(-2*s)}
>>>
Luego se agrupa F(s) por cada elemento de la lista_exp.
# agrupa por cada exp(-s) en lista_exp if len(lista_exp)>0: Fs = sym.expand(Fs,s) Fs = sym.collect(Fs,lista_exp)
Los polos y ceros se obtienen para cada grupo de lista_exp(), empezando por aquellos que no tienen sym.exp(-a*s). Los resultado parciales se almacenan en un diccionario polosceros con el objetivo de mostrar lo que sucede con cada componente y su influencia en F(s).
El análisis detallado de los polos y ceros para la expresión se desarrolla en la sección LTI CT Laplace – H(s) Polos reales y complejos con Sympy-Python . Por ahora para mantener el enfoque sobre el desarrollo del integral se usa una función fcnm.busca_polosceros(Fs) obtenida desde telg1001.py que entrega los polos y ceros para cada componente de sym.exp(-a*s).
Instrucciones con Python – Ejemplos 2, 3, 4 y 5
# Transformada de Laplace Ejemplo 2 y 3 # integral de Laplace unilateral con suma de terminos, # y desplazamientos en tiempo # blog.espol.edu.ec/telg1001/ import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) s = sym.Symbol('s') u = sym.Heaviside(t) # ft = sym.exp(-2*t)*u # ft = 3*sym.exp(-2*t)*u - 2*sym.exp(-t)*u # ft = u # ft = u.subs(t,t-2) ft = u - u.subs(t,t-2) # ft = u.subs(t,t-2) - u.subs(t,t-4) # ft = sym.exp(-2*t)*u + sym.exp(-t)*sym.cos(3*t)*u # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 10 muestras_t = 101 # 51 resolucion grafica # PROCEDIMIENTO fts = ft*sym.exp(-s*t) # f(t,s) para integrar fts = sym.expand(fts) # expresion de sumas fts = sym.powsimp(fts) # simplifica exponentes # Integral Laplace unilateral = True lim_a = 0 # unilateral if not(unilateral): lim_a = -sym.oo Fs_L = sym.integrate(fts,(t,lim_a,sym.oo)) Fs = Fs_L.args[0] # primera ecuacion e intervalo Fs = Fs[0] # solo expresion # convierte a Sympy si es solo constante Fs = sym.sympify(Fs) # separa en lista los sym.exp(-s) lista_exp = list(Fs.atoms(sym.exp(-s))) # agrupa por cada exp(-s) en lista_exp if len(lista_exp)>0: Fs = sym.expand(Fs,s) Fs = sym.collect(Fs,lista_exp) else: Fs = sym.factor(Fs,s) polosceros = fcnm.busca_polosceros(Fs) # SALIDA print(' dentro de integral f(t)*e(-st):') sym.pprint(fts) print('\n expresion F(s):') sym.pprint(Fs) print('\n {Q_polos:veces}: ',polosceros['Q_polos']) print(' {P_ceros:veces}: ',polosceros['P_ceros']) # GRAFICA ------------------ # grafica de f(t) fig_ft = fcnm.graficar_ft(ft,t_a,t_b, muestras = muestras_t, f_nombre='f') # grafica de polos y ceros fig_Fs = fcnm.graficar_Fs(Fs,polosceros['Q_polos'], polosceros['P_ceros'], solopolos=False)) plt.show()
Las instrucciones para las gráficas se pueden simplificar para f(t), usando la instrucción de la función fcnm.graficar_ft() desarrollada en la unidad 3 desde 3.2.1 LTI CT y disponible en telg1001.py.
Para analizar en un gráfico el caso de F(s) en detalle, se requiere realizar las líneas de cada componente que tiene un exp() y los polos para cada componente. Estas instrucciones se desarrollan en la sección LTI CT Laplace – H(s) Polos reales y complejos con Sympy-Python por ahora se usará la función gráfica en telg1001.py
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
..
Ejemplo 4. Transformada de Laplace para suma de términos f(t) con desplazamiento, función «gate» o compuerta causal
Referencia: Lathi práctica 4.1.b p337
literal b. Por integración directa, encuentra la transformada X(s) y la región de convergencia para la función descrita en la imagen
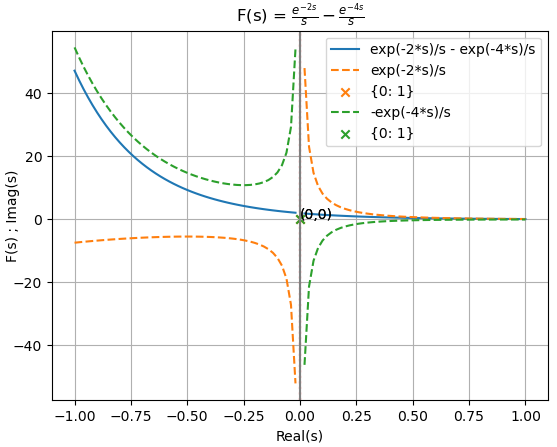
x(t) = \mu (t-2) - \mu (t-4)Con el desarrollo analítico realizado en la pagina anterior se comprueba que el resultado de X(s) es
X(s) = \frac{e^{-2s}}{s}-\frac{e^{-4s}}{s}Desarrollo con Sympy-Python
El bloque de ingreso del ejercicio se actualiza como la suma de escalón unitario μ(t) desplazados,
u = sym.Heaviside(t) ft = u.subs(t,t-2)-u.subs(t,t-4)
obteniendo con el algoritmo el resultado y gráfica correspondiente.
dentro de integral f(t)*e(-st):
-s*t -s*t
- e *Heaviside(t - 4) + e *Heaviside(t - 2)
expresion F(s):
-2*s -4*s
e e
----- - -----
s s
Polos y ceros:
término: exp(-2*s) * 1/s
Q_polos{polos:veces}: {0: 1}
P_ceros{polos:veces}: {}
término: exp(-4*s) * -1/s
Q_polos{polos:veces}: {0: 1}
P_ceros{polos:veces}: {}
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
..
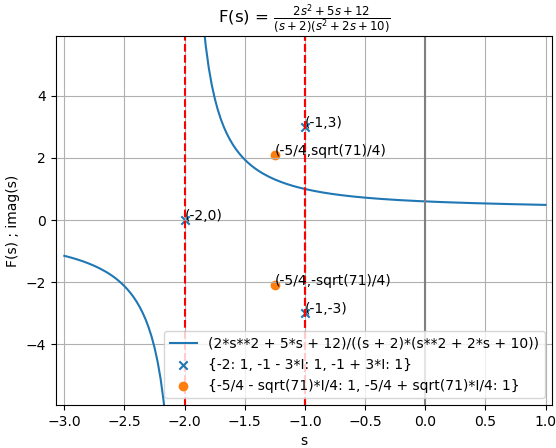
Ejemplo 5. Transformada de Laplace para cos(t)
Referencia: Oppenheim Ejemplo 9.4 p658
Encontrar la transformada de Laplace para:
x(t) = e^{-2t}\mu (t) + e^{-t} \cos (3t) \mu (t)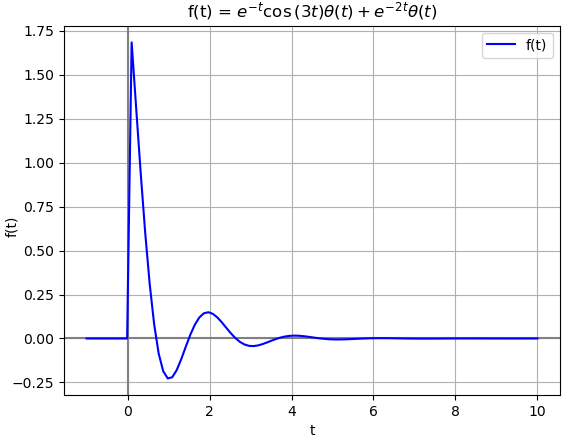
La expresión para el algoritmo de la señal de entrada es:
ft = sym.exp(-2*t)*u + sym.exp(-t)*sym.cos(3*t)*u
el resultado con el algoritmo desarrollado hasta el ejemplo es:
dentro de integral f(t)*e(-st):
-t*(s + 2) -t*(s + 1)
e *Heaviside(t) + e *cos(3*t)*Heaviside(t)
expresion F(s):
2
2*s + 5*s + 12
-----------------------
/ 2 \
(s + 2)*\s + 2*s + 10/
{Q_polos:veces}: {-2: 1, -1 - 3*I: 1, -1 + 3*I: 1}
{P_ceros:veces}: {-5/4 - sqrt(71)*I/4: 1, -5/4 + sqrt(71)*I/4: 1}
La expresión F(s) de factores, también puede expresarse como la suma de fracciones parciales con la instrucción sym.apart() que aplica solo a polinomios. En el caso de tener términos con exp(), la instrucción sym.apart() se puede aplicar por cada grupo.
expresion F(s):
s + 1 1
------------ + -----
2 s + 2
(s + 1) + 9
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
..
Ejemplo 6. Transformada de Laplace con Impulso unitario δ(t) y suma de exponenciales
Referencia: Oppenheim ejemplo 9.5 p661
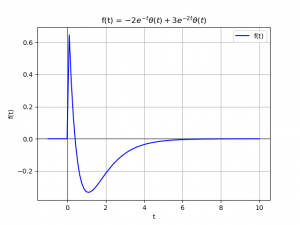
x(t) = \delta(t) -\frac{4}{3} e^{-t} \mu (t) + \frac{1}{3} e^{2t} \mu (t)Los resultados de la parte analítica y con algoritmo del ejercicio se muestran en la gráfica.
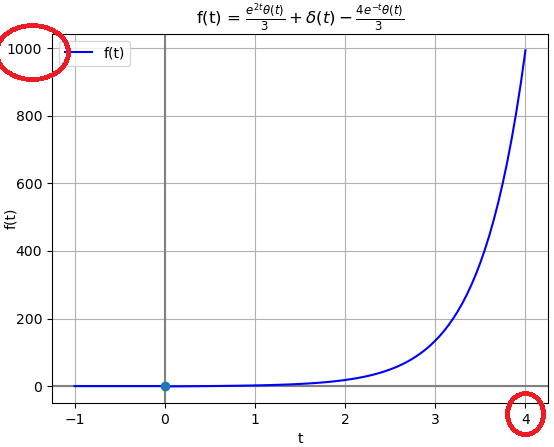
La introducción de un impulso d(t) en el integral de varios componentes ya comienza a generar algun trabajo adicional en la instrucción simbólica sym.integrate(), por lo que es preferible facilitar el desarrollo por cada componente de términos suma. Al entregar a sym.integrate() términos más simples, la función no tiene que analizar varias formas de integración de la expresión, el proceso se acelera y se minimizan errores.
Desarrollo y ajustes en el Algoritmo
Inicialmente considere usar como f(t) = δ(t) y revisar el resultado Fs_L, encontrando que es solo una constante, el resultado de F(s) no es por partes (sym.Piecewise()) como se había realizado hasta ahora en el algoritmo.
Si Fs_L aún es por partes, se puede verificar con la instrucción Fs_L.is_Piecewise que indica True o False para aplicar o no Fs_L[0].
Debe considerar también que el integral unilateral de Laplace presenta el resultado 1/2, en lugar de 1. Revisar las definiciones sobre la función impulso δ(t) en el enlace DiracDelta en Sympy. Para mantener concordancia con lo desarrollado en los textos, se corrige el resultado a 1.
ft = sym.DiracDelta(t)
dentro de integral f(t)*e(-st):
-s*t
e *DiracDelta(t)
expresion F(s):
1/2
{polos:veces}: {}
Para la convención usada en los libros del curso, se revisará si el término al que se aplica el integral de Laplace tiene un impulso para proceder a multiplicarlo por 2. Si el integral fuese de [-∞,∞] el integral tendria resultado 1, pero en lo realizado es solo unilateral (t≥0) por lo que Sympy se ha aplicado básicamente solo la mitad. Discusiones sobre aquello las puede revisar en el sitio web de Sympy.
unilateral = True # Integral del impulso en cero es 1 if fts.has(sym.DiracDelta): donde = fcnm.busca_impulso(fts) if (0 in donde) and unilateral: # (integral unilateral) x 2 fts = fts.subs(d,2*d) fts = sym.powsimp(fts) # simplifica exponentes
con la variable unilateral también se establece el valor del límite inferior del integral:
# Integral Laplace de sumas lim_a = 0 # unilateral if not(unilateral): lim_a = -sym.oo
con lo que se actualiza el resultado anterior a:
ft = sym.DiracDelta(t)
dentro de integral f(t)*e(-st):
-s*t
e *DiracDelta(t)
expresion F(s):
1
{polos:veces}: {}
Nota: Sympy hasta la versión 1.11.1, las operaciones en el dominio ‘s’ para la Transformadas Inversas de Laplace se encuentran implementadas para manejar principalmente números enteros y fracciones. Los resultados de expresiones combinadas con coeficientes enteros y coeficientes reales no necesariamente se simplifican entre si, pues se manejan diferentes dominios ‘ZZ’ o ‘QQ’. (Revisión 2022-Nov)
Para optimizar la simplificación de expresiones con coeficientes entre enteros y reales, los números reales se convierten a su aproximación racional con la instrucción sym.Rational(0.333333).limit_denominator(100).
Convirtiendo los coeficientes a racionales como:
k1 = sym.Rational(1/3).limit_denominator(100) k2 = sym.Rational(4/3).limit_denominator(100) ft = d - k2*sym.exp(-t)*u + k1*sym.exp(2*t)*u
Uniendo las observaciones, el algoritmo más general se muestra a continuación
Instrucciones en Python Ejercicio 6. Transformada de Laplace con impulso δ(t) y suma de exponenciales
# Transformada de Laplace Ejemplo 6 # integral de Laplace unilateral con suma de terminos, # y desplazamientos en tiempo # blog.espol.edu.ec/telg1001/ import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) s = sym.Symbol('s') u = sym.Heaviside(t) d = sym.DiracDelta(t) # ft = u # ft = u.subs(t,t-2) # ft = u - u.subs(t,t-2) # ft = 3*sym.exp(-2*t)*u-2*sym.exp(-t)*u # ft = u.subs(t,t-2) - u.subs(t,t-4) # ft = sym.exp(-2*t)*u + sym.exp(-t)*sym.cos(3*t)*u # ft = d # coeficientes como racional en dominio 'ZZ' enteros k1 = sym.Rational(1/3).limit_denominator(100) k2 = sym.Rational(4/3).limit_denominator(100) ft = d - k2*sym.exp(-t)*u + k1*sym.exp(2*t)*u #ft = u.subs(t,t+1) # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 4 muestras_t = 101 # 51 resolucion grafica # PROCEDIMIENTO def laplace_integral_sumas(ft,unilateral=True): ''' integral de transformada de laplace considera impulsos d(t), escalon u(t) desplazados ''' fts = ft*sym.exp(-s*t) # f(t,s) para integrar fts = sym.expand(fts) # expresion de sumas fts = sym.powsimp(fts) # simplifica exponentes # Integral del impulso en cero es 1 if fts.has(sym.DiracDelta): donde = fcnm.busca_impulso(fts) if (0 in donde) and unilateral: # (integral unilateral) x 2 fts = fts.subs(d,2*d) fts = sym.powsimp(fts) # simplifica exponentes # Integral Laplace de sumas lim_a = 0 # unilateral if not(unilateral): lim_a = -sym.oo Fs = 0*s term_suma = sym.Add.make_args(fts) for term_k in term_suma: # integral Laplace unilateral Fs_L = sym.integrate(term_k,(t,lim_a,sym.oo)) if Fs_L.is_Piecewise: # Fs_L es por partes Fsk = Fs_L.args[0] # primera ecuacion e intervalo Fsk = Fsk[0] # solo expresion else: # una sola expresión Fsk = Fs_L Fs = Fs + Fsk # convierte a Sympy si es solo constante Fs = sym.sympify(Fs) Fs = sym.expand_power_exp(Fs) # lista los sym.exp(-s) lista_exp = list(Fs.atoms(sym.exp(-s))) # agrupa por cada exp(-s) en lista_exp if len(lista_exp)>0: Fs = sym.expand(Fs,s) Fs = sym.collect(Fs,lista_exp) else: Fs = sym.factor(Fs,s) return(Fs) Fs = laplace_integral_sumas(ft, unilateral=True) polosceros = fcnm.busca_polosceros(Fs) # SALIDA print('\n expresion F(s):') sym.pprint(Fs) print('\n {Q_polos:veces}: ',polosceros['Q_polos']) print(' {P_ceros:veces}: ',polosceros['P_ceros'])
La sección de gráficas ya incorpora desde la unidad 3 el caso que f(t) contiene impulsos unitarios, por lo que las instrucciones se mantienen.
# GRAFICA ------------------ #grafica de f(t) fig_ft = fcnm.graficar_ft(ft,t_a,t_b, muestras = muestras_t, f_nombre='f') # grafica de polos y ceros fig_Fs = fcnm.graficar_Fs(Fs,polosceros['Q_polos'], polosceros['P_ceros'], solopolos=False) plt.show()
Presentando así, un algoritmo general para desarrollar integrales de Laplace.
Desde luego existe la forma mas simple de usar con las instrucciones Fs_L = sym.laplace_transform(ft,t,s) mencionadas al inicio de la página. El algoritmo es un ejercicio didáctico de cómo realizar la tabla de pares de transformadas.
En la siguiente sección el algoritmo se simplifica y se muestra el uso de las transformadas de Laplace usando las librerías de Sympy.
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]
Ejemplo 7. Transformada de Laplace de Impulsos unitarios desplazados
Referencia: Lathi Ej 4.9c p355
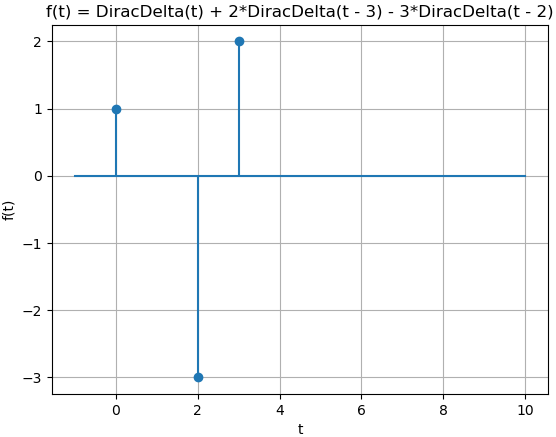
Considera la entrada x(t) como una suma de impulsos desplazados en tiempo y de diferente magnitud.
x(t) = \delta (t) - 3 \delta (t-2) + 2 \delta (t-3)para el algoritmo del ejercicio 6, se modifica la línea de ingreso a:
ft = d - 3*d.subs(t,t-2) + 2*d.subs(t,t-3)
obteniendo como resultado del algoritmo anterior:
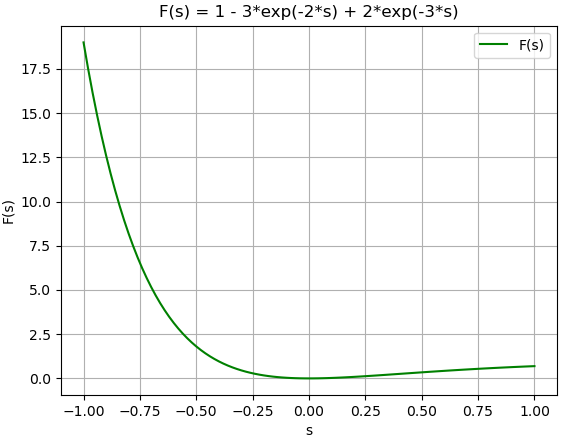
X(s) = 1 - 3 e^{-2s} + 2 e^{-3s} dentro de integral f(t)*e(-st):
-s*t -s*t -s*t
e *DiracDelta(t) + 2*e *DiracDelta(t - 3) - 3*e *DiracDelta(t - 2)
expresion F(s):
-2*s -3*s
1 - 3*e + 2*e
{Q_polos:veces}: {}
con las siguientes gráficas:
y para F(s):
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 suma de términos ] [ ej3 escalón desplazado ] [ ej4 desplazados ] [ ej5 coseno ] [ ej6 impulso ] [ ej7 impulsos desplazados ]