Se desarrolla el integral de convolución con Sympy con los criterios indicados en el desarrollo analítico. Para determinar los límites del integral se requiere revisar la Causalidad de h(t) descrita con la función es_causal(ft). Los pasos para los resultados se completan con la función desarrollada en la sección anterior para Integral de convolución.
..
Ejemplo 1. Convolución con x(t) causal y h(t) causal
Referencia: Lathi ejemplo 2.9 p175, Lathi ejemplo 2.6 p166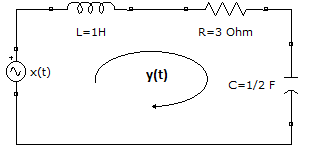
En la entrada de sistema se aplica:
x(t) = 10 e^{-3t} \mu (t)El sistema tiene respuesta a impulso:
h(t) = \big( 2e^{-2t} -e^{-t}\big)\mu (t)El ejemplo es la continuación de lo realizado en respuesta a entrada cero, que tiene la ecuación:
(D^2 + 3D +2)y(t) = Dx(t)La respuesta del sistema y(t) para un LTIC se determina como:
y(t) = x(t) \circledast h(t) = \int_{-\infty}^{+\infty} x(\tau)h(t-\tau) \delta \tauSi la entrada x(t) y el sistema h(t) son causales, la respuesta también será causal. Teniendo como límites del integral τa = 0 y τb = t
y(t)=\begin{cases}\int_{0^{-}}^{t} x(\tau)h(t-\tau) \delta \tau , & t\ge 0\\ 0, & t<0 \end{cases}El límite inferior del integral se usa como 0–, implica aunque se escriba solo 0 se pretende evitar la dificultad cuando x(t) tiene un impulso en el origen.
Para iniciar el algoritmo se definen las variables t y tau, simplificando la expresión del escalón unitario o Heaviside con u.
# INGRESO t = sym.Symbol('t',real=True) tau = sym.Symbol('tau',real=True) u = sym.Heaviside(t)
Se definen las señales de entrada x(t) y respuesta al impulso h(t) usando las expresiones en Sympy. Para seleccionar los límites del integral de convolución se indica si x(t) y h(t) son causales.
# entrada x(t), respuesta impulso h(t)
x = 10*sym.exp(-3*t)*u
h = (2*sym.exp(-2*t)-sym.exp(-t))*u
Se realiza la comprobación de causalidad revisando cada término de la función, que contenga un escalón o un impulso, tomando como referencia la forma en que se construye h(t) con el impulso y los modos caraterísticos.
xcausal = fcnm.es_causal(x) hcausal = fcnm.es_causal(h)
En el procedimiento se definen los límites del integral de convolución, la expresión dentro del integral xh(t) y con el resultado se aplica la instrucción expand() para obtener términos suma mas sencillos.
En el caso que la respuesta al impulso h(t) no sea causal y la entrada x(t) es causal, se intercambian las funciones para mantener la simplicidad del integral con límite superior t en lugar de infinito. Se aplica la propiedad conmutativa de la convolución.
# intercambia si h(t) no es_causal # con x(t) es_causal por propiedad conmutativa intercambia = False if hcausal==False and xcausal==True: temporal = h h = x x = temporal xcausal = False hcausal = True intercambia = True # limites de integral de convolución tau_a = -sym.oo ; tau_b = sym.oo if hcausal==True: tau_b = t if (xcausal and hcausal)==True: tau_a = 0
Se añaden las instrucciones al algoritmo del ejercicio para la convolución de la sección anterior y convierte a una función respuesta_ZSR(x,h) .
Con los resultados del algoritmo, queda añadir las instrucciones para mostrar las ecuaciones y las gráficas como los siguientes:
Resultados con Python
xh :
-t -2*tau
- 10*e *e *Heaviside(tau)*Heaviside(t - tau) +
-2*t -tau
+ 20*e *e *Heaviside(tau)*Heaviside(t - tau)
xcausal : True
hcausal : True
[tau_a,tau_b] : [0, t]
intercambia : False
cond_graf : True
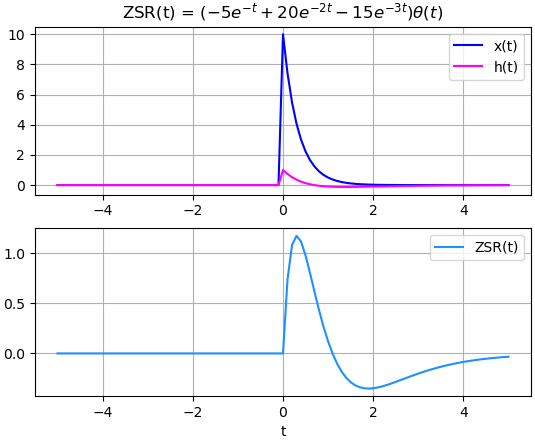
ZSR :
/ -t -2*t -3*t\
\- 5*e + 20*e - 15*e /*Heaviside(t)
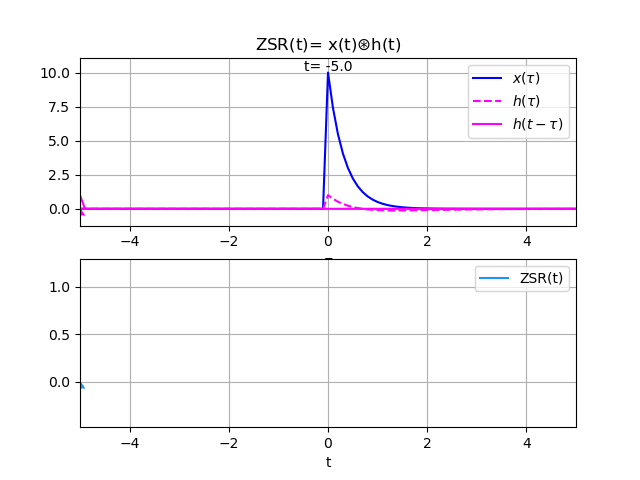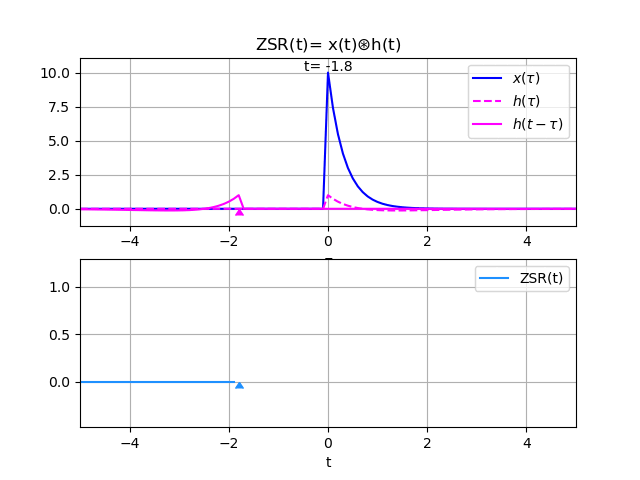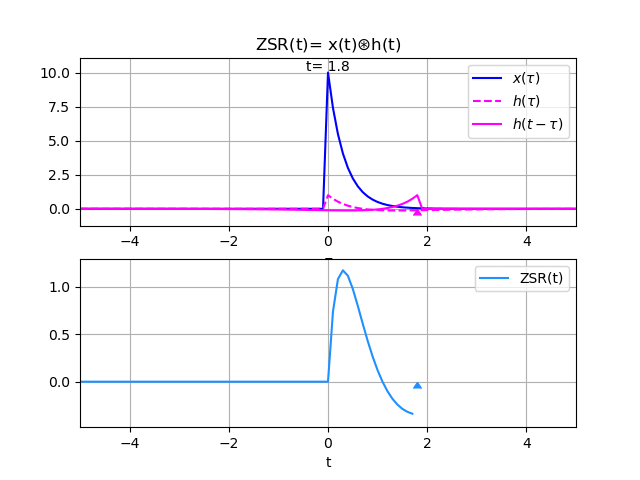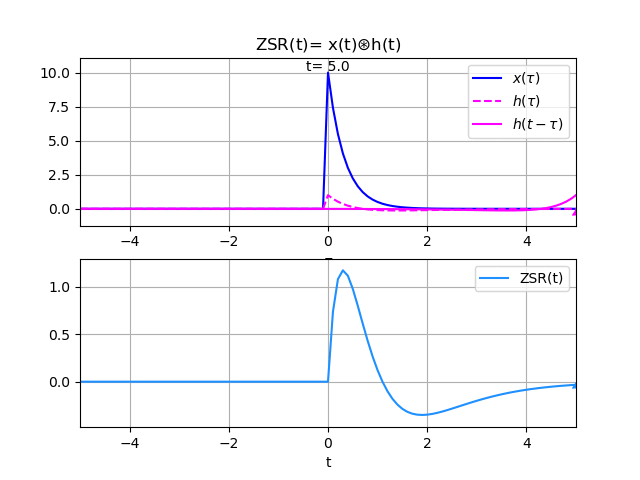
Grafica animada de la convolución
Instrucciones en Python
# Respuesta estado cero ZSR con x(t) y h(t) # Integral de convolucion con Sympy # http://blog.espol.edu.ec/telg1001/lti-ct-respuesta-a-estado-cero-con-sympy-python/ import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) tau = sym.Symbol('tau',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t), respuesta impulso h(t) x = 10*sym.exp(-3*t)*u h = (2*sym.exp(-2*t)-sym.exp(-t))*u # grafica intervalo [t_a,t_b] plano simétrico t_b = 5 ; t_a = -t_b muestras = 101 # PROCEDIMIENTO def respuesta_ZSR(x,h): '''Respuesta a estado cero x(t) y h(t) ''' # revisa causalidad de señales xcausal = fcnm.es_causal(x) hcausal = fcnm.es_causal(h) # intercambia si h(t) no es_causal # con x(t) es_causal por propiedad conmutativa intercambia = False if hcausal==False and xcausal==True: temporal = h h = x x = temporal xcausal = False hcausal = True intercambia = True # limites de integral de convolución tau_a = -sym.oo ; tau_b = sym.oo if hcausal==True: tau_b = t if (xcausal and hcausal)==True: tau_a = 0 # integral de convolución x(t)*h(t) xh = x.subs(t,tau)*h.subs(t,t-tau) xh = sym.expand(xh,t) ZSR = sym.integrate(xh,(tau,tau_a,tau_b)) ZSR = sym.expand(ZSR,t) if not(ZSR.has(sym.Integral)): ZSR = fcnm.simplifica_escalon(ZSR) lista_escalon = ZSR.atoms(sym.Heaviside) ZSR = sym.expand(ZSR,t) # terminos suma ZSR = sym.collect(ZSR,lista_escalon) if intercambia == True: xcausal = True hcausal = False # graficar si no tiene Integral o error cond_graf = ZSR.has(sym.Integral) cond_graf = cond_graf or ZSR.has(sym.oo) cond_graf = cond_graf or ZSR.has(sym.nan) cond_graf = not(cond_graf) sol_ZSR = {'xh' : xh, 'xcausal' : xcausal, 'hcausal' : hcausal, '[tau_a,tau_b]': [tau_a,tau_b], 'intercambia' : intercambia, 'cond_graf' : cond_graf, 'ZSR' : ZSR,} return(sol_ZSR) sol_ZSR = respuesta_ZSR(x,h) ZSR = sol_ZSR['ZSR'] # SALIDA fcnm.print_resultado_dict(sol_ZSR) if sol_ZSR['hcausal']==False: print('revisar causalidad de h(t)') if sol_ZSR['xcausal']==False: print('revisar causalidad de x(t)') if sol_ZSR['intercambia']: print('considere intercambiar h(t)con x(t)') if not(sol_ZSR['cond_graf']): print('revisar acortar x(t) o h(t) para BIBO') # GRAFICA if sol_ZSR['cond_graf']: fig_xh_y = fcnm.graficar_xh_y(x,h,ZSR,t_a,t_b, muestras,y_nombre='ZSR') #plt.show() # grafica animada de convolución n_archivo = '' # sin crear archivo gif animado # n_archivo = 'LTIC_ZSR_Ej01' # requiere 'imagemagick' if sol_ZSR['cond_graf']: figura_animada = fcnm.graf_animada_xh_y(x,h,ZSR,t_a,t_b, muestras, reprod_x = 4,y_nombre='ZSR', archivo_nombre = n_archivo) plt.show()
[ ejemplo 1. x(t) y h(t) causal ] [ ejemplo 2. h(t) causal ] [ ejemplo 3. x(t) y h(t) causal]
..
Ejemplo 2. Respuesta entrada cero ZSR entre exponencial y escalón unitario
Referencia: Oppenheim Ej 2.6 p98
Sea la y(t) la respuesta a entrada cero entre las siguientes señales:
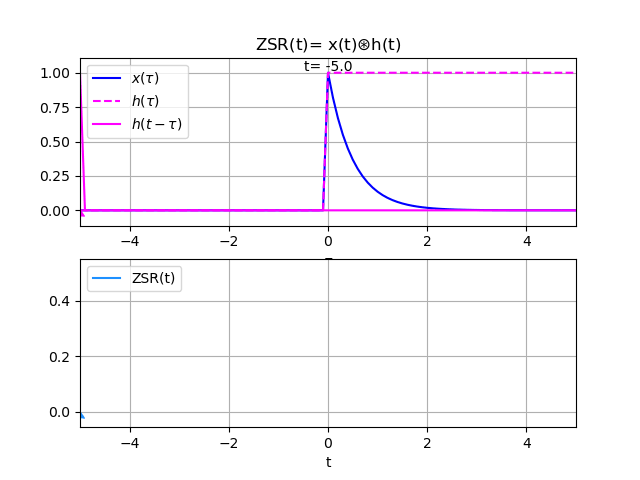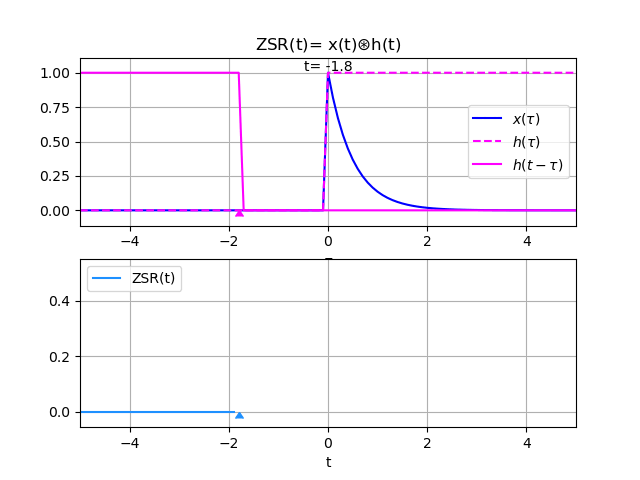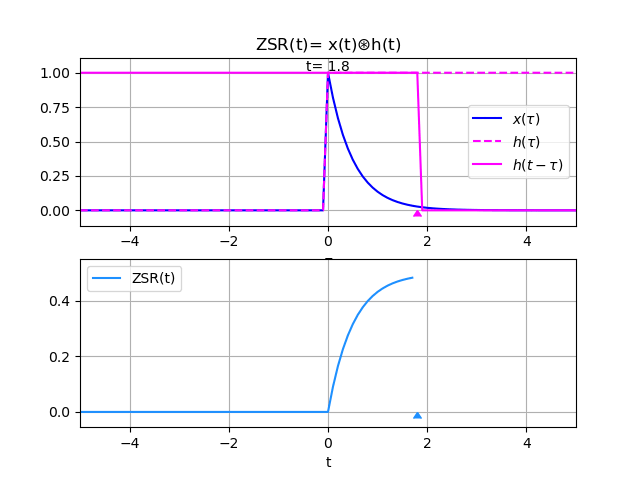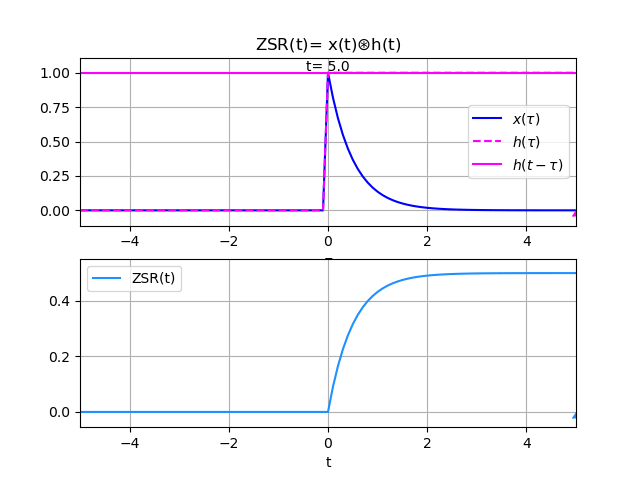
x(t) = e^{-2t} \mu (t) h(t) = \mu (t)Para interpretar el integral de convolución en el ejercicio aa desarrollar se adjunta la animación siguiente:
Las funciones para el algoritmo se describen como:
# entrada x(t), respuesta impulso h(t)
x = sym.exp(-2*t)*u
h = u
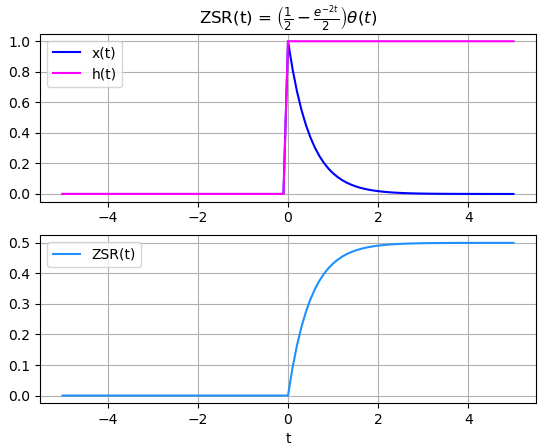
Teniendo como resultado:
xh : -2*tau e *Heaviside(tau)*Heaviside(t - tau) xcausal : True hcausal : True [tau_a,tau_b] : [0, t] intercambia : False cond_graf : True ZSR : / -2*t\ |1 e | |- - -----|*Heaviside(t) \2 2 /
Gráfica de algoritmo
[ ejemplo 1. x(t) y h(t) causal ] [ ejemplo 2. h(t) causal ] [ ejemplo 3. x(t) y h(t) causal]
..
Ejemplo 3. Ejercicio con Filtros
Tarea: Lathi 2.6-4 filtros p207
Para pruebas de algoritmo
[ ejemplo 1. x(t) y h(t) causal ] [ ejemplo 2. h(t) causal ] [ ejemplo 3. x(t) y h(t) causal]