Para encontrar la Respuesta a entrada cero del sistema lineal del Modelo entrada-salida,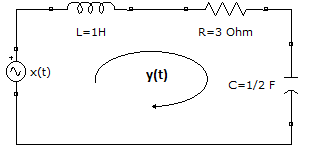 
representado por un circuito, se plantea la ecuación diferencial lineal escrita desde el termino de mayor orden. Por ejemplo:
Luego se se simplifica haciendo x(t)=0, obteniendo ecuación complementaria relacionada a la forma homogénea de la ecuación diferencial.
\frac{d^2}{dt^2}y(t) +3\frac{d}{dt}y(t) + 2y(t) = 0
.. ..
Ejemplo 1. Respuesta a entrada cero ZIR para un sistema LTI CT – Desarrollo analítico con Sympy
Referencia: Lathi Ejemplo 2.1.a p155, Oppenheim 2.4.1 p117, ejemplo 1 de Modelo entrada-salida, Sympy ODE solver
E
l circuito que representa la respuesta a entrada cero tiene x(t)=0 como se muestra en la figura.
La ecuación diferencial con operadores D es:
(D^2 + 3D +2)y(t) = 0Adicionalmente, para el desarrollo se indican las condiciones iniciales y'(0)=-5, y(0)=0.
La librería Sympy-Python permite usar expresiones de derivadas en forma simbólica y resolverlas siguiendo los pasos seguidos en la solución analítica.
Para iniciar el algoritmo, se define la variable independiente t como un símbolo y las función matemática y(t) para la salida y x(t) para la entrada.
La ecuación diferencial se escribe siguiendo el orden de los lados de expresión denominados para la parte izquierda, LHS, y la parte derecha, RHS.
import sympy as sym # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') # ecuacion EDO: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,evaluate=False) ecuacion_edo = sym.Eq(LHS,RHS) # condiciones iniciales [y'(t0),y(t0)] t0 = 0 cond_inicio = [-5,0]
Las condiciones iniciales y’(0)=-5, y(0)=0 , se agrupan en una lista cond_inicio=[y'(t0),y(t0)] siguiendo el orden descendente de derivada, semejante al orden seguido al escribir la ecuación diferencial. El orden usado facilita la compatibilidad con las soluciones numéricas a realizar con Scipy-Python.
Solución general de la ecuación diferencial lineal homogénea
Se obtiene la ecuación homogénea aplicando x(t)=0 al lado derecho de la ecuación diferencial (RHS).
La solución general de la EDO se obtiene mediante la instrucción sym.dsolve() aplicada a la ecuación, indicando que se busca resolver para y(t). Para facilitar el procesamiento con Sympy, las ecuaciones se expresan con términos mas simples de sumas, aplicando la instrucción sym.expand().
# ecuacion homogenea x(t)=0, entrada cero RHSx0 = ecuacion.rhs.subs(x(t),0).doit() LHSx0 = ecuacion.lhs.subs(x(t),0).doit() homogenea = LHSx0 - RHSx0 # solucion general entrada cero general = sym.dsolve(homogenea, y(t)) general = general.expand()
Con lo que se obtiene la solución general mostrada con sym.pprint():
-t -2*t y(t) = C1*e + C2*e
Las condiciones iniciales se aplican a la solución general para encontrar la solución homogenea o ZIR. Para aplicar cada condición inicial se usa el lado derecho (.rhs )de la ecuación general, por ejemplo:
Se realiza lo mismo para y(0)=0
Cada condición inicial genera una ecuación que se agrupa en un sistema de ecuaciones, eq_condicion=[]. El sistema de ecuaciones se resuelve con la instrucción sym.solve(), que entrega las constantes para las incógnitas C1 y C2 en un dicionario.
# aplica condiciones iniciales N = sym.ode_order(LHS,y) # orden Q(D) eq_condicion = [] for k in range(0,N,1): ck = cond_inicio[(N-1)-k] dyk = general.rhs.diff(t,k) dyk = dyk.subs(t,t0) eq_k = sym.Eq(ck,dyk) eq_condicion.append(eq_k) constante = sym.solve(eq_condicion)
El resultado de eq_condicion y las constantes obtenidas se muestra a continuación
0 = C1 + C2
-5 = -C1 - 2*C2
{C1: -5, C2: 5}
La solución homogénea o ZIR de la ecuación diferencial se obtiene al sustituir las constantes encontradas en la ecuación general.
# reemplaza las constantes en general y_c = general for Ci in constante: y_c = y_c.subs(Ci, constante[Ci]) # ecuacion complementaria o respuesta a entrada cero ZIR ZIR = y_c.rhs
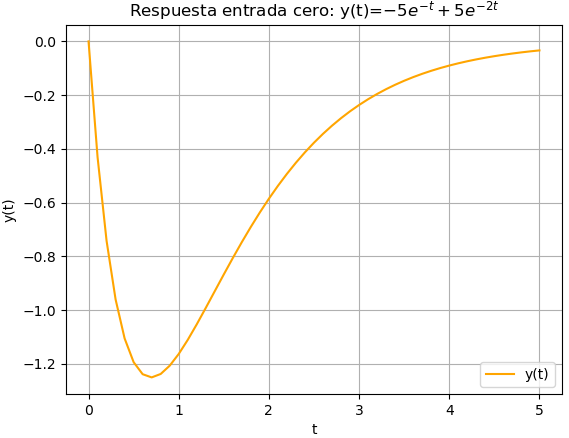
obteniendo solución a la ecuación homogena ‘y‘, o respuesta a entrada cero ZIR, mostrada con sym.pprint(y_homogenea). Para ZIR se toma el dado derecho de y_homogenea.
-t -2*t y(t) = - 5*e + 5*ey(t) = -5 e^{-t} + 5 e^{-2t}
resultado del algoritmo:
ecuación diferencial a resolver:
2
d d d
2*y(t) + 3*--(y(t)) + ---(y(t)) = --(x(t))
dt 2 dt
dt
clasifica EDO:
factorable
nth_linear_constant_coeff_variation_of_parameters
nth_linear_constant_coeff_variation_of_parameters_Integral
ecuación diferencial homogenea:
2
d d
2*y(t) + 3*--(y(t)) + ---(y(t)) = 0
dt 2
dt
Solución general:
-t -2*t
y(t) = C1*e + C2*e
Ecuaciones de condiciones iniciales:
0 = C1 + C2
-5 = -C1 - 2*C2
constantes en solucion general: {C1: -5, C2: 5}
ZIR(t):
-t -2*t
- 5*e + 5*e
>>>
Instrucciones en Python
# Respuesta a entrada cero ZIR con Sympy # Lathi 2.1.a pdf 155, (D^2+ 3D + 2)y = Dx import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,1,evaluate=False) ecuacion = sym.Eq(LHS,RHS) # condiciones iniciales [y'(t0),y(t0)] t0 = 0 cond_inicio = [-5,0] # PROCEDIMIENTO edo_tipo = sym.classify_ode(ecuacion, y(t)) # ecuación homogénea x(t)=0, entrada cero RHSx0 = ecuacion.rhs.subs(x(t),0).doit() LHSx0 = ecuacion.lhs.subs(x(t),0).doit() homogenea = LHSx0 - RHSx0 # solucion general de ecuación homogénea general = sym.dsolve(homogenea, y(t)) general = general.expand() # aplica condiciones iniciales N = sym.ode_order(ecuacion,y(t)) # orden Q(D) eq_condicion = [] for k in range(0,N,1): ck = cond_inicio[(N-1)-k] dyk = general.rhs.diff(t,k) dyk = dyk.subs(t,t0) eq_k = sym.Eq(ck,dyk) eq_condicion.append(eq_k) constante = sym.solve(eq_condicion) # reemplaza las constantes en general y_c = general for Ci in constante: y_c = y_c.subs(Ci, constante[Ci]) # respuesta a entrada cero ZIR ZIR = y_c.rhs # SALIDA print('ecuación diferencial a resolver: ') sym.pprint(ecuacion) print('clasifica EDO:') for elemento in edo_tipo: print(' ',elemento) print('ecuación diferencial homogenea: ') sym.pprint(homogenea) print('\nSolución general: ') sym.pprint(general) print('\nEcuaciones de condiciones iniciales:') for eq_k in eq_condicion: sym.pprint(eq_k) print('constantes en solucion general: ', constante) print('\nZIR(t):') sym.pprint(ZIR)
Gráfica de respuesta a entrada cero ZIR
Adicionalmente se realiza la gráfica, convirtiendo la ecuación de forma simbólica a forma numérica numpy con sym.lambdify(t,ZIR,'numpy').
Se establece el intervalo de observación entre t_a=0 y t_b=5 para evaluar la función y se envia a graficar, con el suficiente número de muestras para que la gráfica se muestre suave.
Se añaden las siguientes instrucciones al algoritmo anterior:
# GRAFICA ------------------ import numpy as np import matplotlib.pyplot as plt # INGRESO t_a = 0 ; t_b = 5 # intervalo tiempo [t_a,t_b] muestras = 51 # PROCEDIMIENTO yt = sym.lambdify(t,ZIR, modules=equivalentes) ti = np.linspace(t_a,t_b,muestras) yi = yt(ti) # Grafica plt.plot(ti,yi, color='orange', label='ZIR(t)') untitulo = 'ZIR(t)=$'+ str(sym.latex(ZIR))+'$' plt.title(untitulo) plt.xlabel('t') plt.ylabel('ZIR(t)') plt.legend() plt.grid() plt.show()
Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python ] [Runge-Kutta d2y/dx2] [Simulador]
Ejemplo 2. Respuesta a entrada cero ZIR con raíces características repetidas
Referencia: Lathi Ejemplo 2.1.b p155
Encontrar y0(t), la respuesta a entrada cero para un sistema LTI CT descrito por la ecuación diferencial lineal de orden 2:
(D^2 + 6D +9)y(t) = (3D+5)x(t)con las condiciones iniciales y(0) = 3, y'(0)=-7
El sistema tiene un polinomio característico de raíces repetidas. El resultado usando el algoritmo se muestra a continuación:
clasifica EDO:
factorable
nth_linear_constant_coeff_variation_of_parameters
nth_linear_constant_coeff_variation_of_parameters_Integral
homogenea :
2
d d
9*y(t) + 6*--(y(t)) + ---(y(t)) = 0
dt 2
dt
general :
-3*t -3*t
y(t) = C1*e + C2*t*e
eq_condicion :
3 = C1
-7 = -3*C1 + C2
constante : {C1: 3, C2: 2}
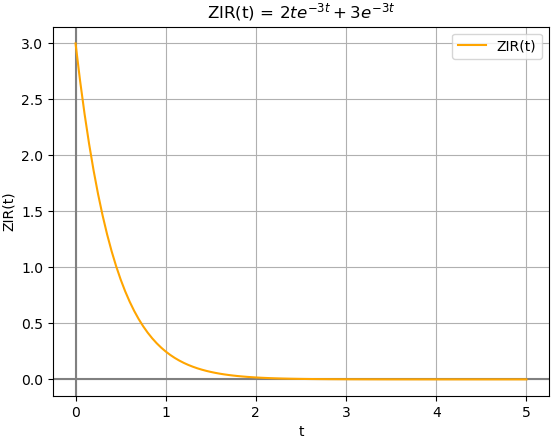
ZIR :
-3*t -3*t
2*t*e + 3*e
Instrucciones en Python
Se reordena el algoritmo del ejercicio anterior para disponer de funciones que simplifiquen las instrucciones principales para obtener las respuestas de los ejercicios. Se crean las funciones respuesta_ZIR() y graficar_ft() que luego pasarán a ser parte de los algoritmos del curso en telg1001.py.
Para las definiciones de RHS y LHS dentro de la función se usa ecuación.rhs y ecuacion.lhs.
En el diccionario solución, se incorpora la respuesta en la entrada 'ZIR'.
# Respuesta a entrada cero ZIR con Sympy-Python # http://blog.espol.edu.ec/telg1001/lti-ct-respuesta-entrada-cero-con-sympy-python/ # Lathi 2.1.b pdf 155, (D^2+ 6D + 9)y = (3D+5)x import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 6*sym.diff(y(t),t,1) + 9*y(t) RHS = 3*sym.diff(x(t),t,1,evaluate=False)+5*x(t) ecuacion = sym.Eq(LHS,RHS) # condiciones iniciales [y'(t0),y(t0)] t0 = 0 cond_inicio = [-7,3] # Grafica: intervalo tiempo [t_a,t_b] t_a = 0 ; t_b = 5 muestras = 51 # PROCEDIMIENTO def respuesta_ZIR(ecuacion,cond_inicio=[],t0, y = sym.Function('y'),x = sym.Function('x')): ''' Sympy: ecuacion: diferencial en forma(LHS,RHS), condiciones de inicio t0 y [y'(t0),y(t0)] cond_inicio en orden descendente derivada ''' # ecuacion homogenea x(t)=0, entrada cero RHSx0 = ecuacion.rhs.subs(x(t),0).doit() LHSx0 = ecuacion.lhs.subs(x(t),0).doit() homogenea = LHSx0 - RHSx0 # solucion general entrada cero general = sym.dsolve(homogenea,y(t)) general = general.expand() # aplica condiciones iniciales N = sym.ode_order(ecuacion,y(t)) # orden Q(D) eq_condicion = [] for k in range(0,N,1): ck = cond_inicio[(N-1)-k] dyk = general.rhs.diff(t,k) dyk = dyk.subs(t,t0) eq_k = sym.Eq(ck,dyk) eq_condicion.append(eq_k) constante = sym.solve(eq_condicion) # reemplaza las constantes en general y_c = general for Ci in constante: y_c = y_c.subs(Ci, constante[Ci]) # respuesta a entrada cero ZIR ZIR = y_c.rhs sol_ZIR = {'homogenea' : sym.Eq(homogenea,0), 'general' : general, 'eq_condicion': eq_condicion, 'constante' : constante, 'ZIR' : ZIR,} return(sol_ZIR) edo_tipo = sym.classify_ode(ecuacion, y(t)) # Respuesta entrada cero ZIR sol_ZIR = respuesta_ZIR(ecuacion,cond_inicio,t0) ZIR = sol_ZIR['ZIR'] # SALIDA print('clasifica EDO:') for elemento in edo_tipo: print(' ',elemento) fcnm.print_resultado_dict(sol_ZIR) # GRAFICA ------------------ figura_ZIR = fcnm.graficar_ft(ZIR,t_a,t_b,muestras,'ZIR') plt.show()
Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python ] [Runge-Kutta d2y/dx2] [Simulador]
..
Ejemplo 3. EDO y respuesta a entrada cero ZIR con raíces complejas
Referencia: Lathi Ejemplo 2.1.c p155
Encontrar y0(t), la respuesta a entrada cero para un sistema LTI CT descrito por la ecuación diferencial ordinaria de orden 2:
(D^2 + 4D +40)y(t) = (D+2)x(t)con condiciones iniciales y(0) = 2, y'(0)=16.78
Tarea: Use el algoritmo del ejercicio anterior y modifique lo necesario para realizar el ejercicio. Realice el desarrollo analítico en papel y lápiz y compare. En caso de ser necesario, proponga mejoras al algoritmo presentado.
Los resultados con el algoritmo son:
ecuación diferencial a resolver:
2
d d d
40*y(t) + 4*--(y(t)) + ---(y(t)) = 2*x(t) + --(x(t))
dt 2 dt
dt
ecuación diferencial homogenea:
2
d d
40*y(t) + 4*--(y(t)) + ---(y(t)) = 0
dt 2
dt
Solución general:
-2*t -2*t
y(t) = C1*e *sin(6*t) + C2*e *cos(6*t)
Ecuaciones de condiciones iniciales:
2 = C2
16.78 = 6*C1 - 2*C2
constantes en solución general: {C1: 3.46333333333333, C2: 2.00000000000000}
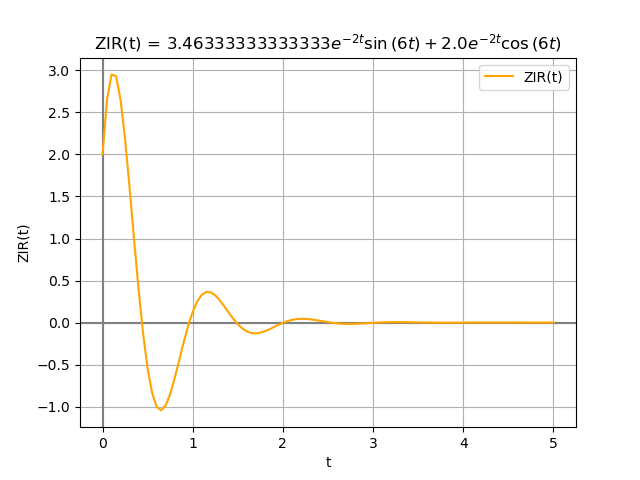
Solución ZIR:
-2*t -2*t
3.46333333333333*e *sin(6*t) + 2.0*e *cos(6*t)
>>>
Instrucciones con Python
# Respuesta a entrada cero ZIR con Sympy-Python # http://blog.espol.edu.ec/telg1001/lti-ct-respuesta-entrada-cero-con-sympy-python/ # Lathi 2.1.c pdf 155, (D^2+ 4D + 40)y = (D+2)x import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 4*sym.diff(y(t),t,1) + 40*y(t) RHS = sym.diff(x(t),t,1,evaluate=False)+2*x(t) ecuacion = sym.Eq(LHS,RHS) # condiciones iniciales [y'(t0),y(t0)] t0 = 0 cond_inicio = [16.78,2] # Grafica: intervalo tiempo [t_a,t_b] t_a = 0 ; t_b = 5 muestras = 51 # PROCEDIMIENTO edo_tipo = sym.classify_ode(ecuacion, y(t)) # Respuesta entrada cero ZIR sol_ZIR = fcnm.respuesta_ZIR(ecuacion,cond_inicio,t0) ZIR = sol_ZIR['ZIR'] # SALIDA print('clasifica EDO:') for elemento in edo_tipo: print(' ',elemento) fcnm.print_resultado_dict(sol_ZIR) # GRAFICA ------------------ figura_ZIR = fcnm.graficar_ft(ZIR,t_a,t_b,muestras,'ZIR') plt.show()
Resumen de funciones de Señales y Sistemas telg1001.py
Las funciones desarrolladas para uso posterior se agrupan en un archivo resumen telg1001.py.
Use una copia del archivo como telg1001.py en el directorio de trabajo, e incorpore las funciones con import y use en el algoritmo llamando a la funcion con fcnm.funcion().
iimport telg1001 as fcnm respuesta = fcnm.funcion(parametros)
Al desarrollar más funciones en cada unidad, se incorporan al archivo del curso de Señales y Sistemas.
Mostrar el resultado del diccionario según el tipo de entrada
Para mostrar los resultados de una forma más fácil de leer, se usará sym.pprint() para las ecuaciones, y print() para los demás elementos del resultado
def print_resultado_dict(resultado): ''' print de diccionario resultado formato de pantalla ''' eq_sistema = ['ZIR','h','ZSR','xh'] for entrada in resultado: tipo = type(resultado[entrada]) cond = (tipo == sym.core.relational.Equality) cond = cond or (entrada in eq_sistema) if cond: print(entrada,':') sym.pprint(resultado[entrada]) elif tipo==list or tipo==tuple: tipoelem = type(resultado[entrada][0]) if tipoelem==sym.core.relational.Equality: print(entrada,':') for fila in resultado[entrada]: sym.pprint(fila) else: print(entrada,':') for fila in resultado[entrada]: print(' ',fila) else: print(entrada,':',resultado[entrada]) return()