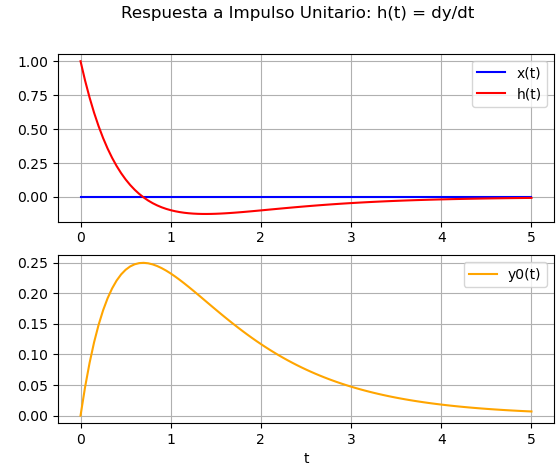
2. Respuesta a impulso con sistema LTI definido en Scipy.signal
La libreria Scipy.signal permite definir un sistema LTI, usando los coeficientes de la ecuación P, Q y las condiciones de inicio. La respuesta a un impulso unitario δ(t) o función de transferencia h(t) se calcula con una versión muestreada xi a partir del tiempo muestreado en el intervalo [a,b].
sistema = senal.lti(P,Q)
# respuesta a impulso
[t_h, hi] = sistema.impulse(T = ti)
Del problema del «Sistema LTIC – Modelo entrada-salida» y la ecuación de segundo orden, se tiene dos opciones para la respuesta:
– scipy.signal.impulse() donde solo se da el vector ti
– aplicar la teoria de los coeficientes donde solo la derivada de mayor orden de P(D) evaluada en cero, tiene el valor de uno. Todos los demás términos tienen el valor de cero. Revisar la parte conceptual de la sección para respuesta a impulso.
Para el ejercicio y como comprobación se calculan las dos formas, con entrada cero y condición inicial [1,0] y con la función de scipy, que son las usadas en la gráfica.
Instrucciones en Python
# Sistema lineal usando scipy.signal # Q(D)y(t)=P(D)x(t) # ejemplo: (D^2+3D+2)y(t)=(D+0)x(t) import numpy as np import scipy.signal as senal import matplotlib.pyplot as plt # INGRESO # Señal de entrada x(t) x = lambda t: t*0 # Sistema LTI # coeficients Q P de la ecuación diferencial Q = [1., 3., 2.] P = [1., 0.] # condiciones iniciales [y'(0),y(0)] cond_inicio = [1,0] # grafica, parametros a = 0 ; b = 5 # intervalo observacion [a,b] muestras = 101 # PROCEDIMIENTO # intervalo observado ti = np.linspace(a, b, muestras) xi = x(ti) sistema = senal.lti(P,Q) # respuesta entrada cero [t_y, yi, yc] = senal.lsim(sistema, xi, ti, cond_inicio) # respuesta a impulso [t_h, hi] = sistema.impulse(T = ti) # SALIDA - GRAFICA plt.subplot(211) plt.suptitle('Respuesta a Impulso Unitario: h(t) = dy/dt') plt.plot(ti, xi, color='blue', label='x(t)') plt.plot(t_h, hi, color='red', label='h(t)') plt.legend() plt.grid() plt.subplot(212) # plt.plot(t_y, yi, color='magenta', label='y(t)') # plt.plot(t_y, yc[:,0], 'b-.', label='h(t)') plt.plot(t_y, yc[:,1], color='orange', label='y0(t)') plt.xlabel('t') plt.legend() plt.grid() plt.show()
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]
..
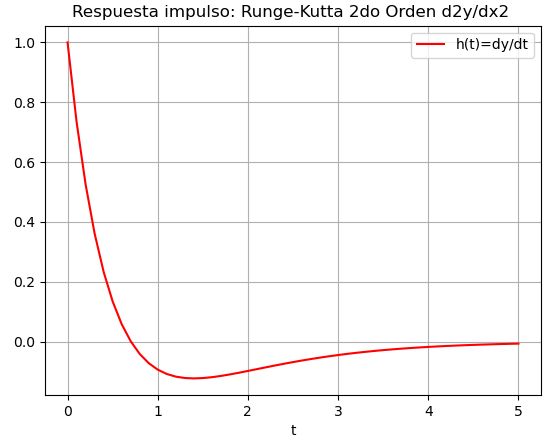
3. Algoritmo de Runge-Kutta d2y/dx2 de Análisis numérico
Para el caso del algoritmo de Runge-Kutta, se aplica las condiciones iniciales de y(0)= 0 y y'(0)=1,
siguiendo lo descrito en la parte teórica y se toman los valores de z=y’ para obtener el resultado.
Las instrucciones aplicadas al algoritmo de entrada cero se muestran a continuación:
Instrucciones en Python
# Respuesta a entrada cero # solucion para (D^2+ D + 1)y = 0 import numpy as np import matplotlib.pyplot as plt def rungekutta2_fg(f,g,x0,y0,z0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,3),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0,z0] xi = x0 yi = y0 zi = z0 for i in range(1,tamano,1): K1y = h * f(xi,yi,zi) K1z = h * g(xi,yi,zi) K2y = h * f(xi+h, yi + K1y, zi + K1z) K2z = h * g(xi+h, yi + K1y, zi + K1z) yi = yi + (K1y+K2y)/2 zi = zi + (K1z+K2z)/2 xi = xi + h estimado[i] = [xi,yi,zi] return(estimado) # PROGRAMA f = lambda t,y,z: z g = lambda t,y,z: -3*z -2*y t0 = 0 y0 = 0 z0 = 1 h = 0.1 tn = 5 muestras = int((tn-t0)/h) tabla = rungekutta2_fg(f,g,t0,y0,z0,h,muestras) ti = tabla[:,0] yi = tabla[:,1] zi = tabla[:,2] # SALIDA np.set_printoptions(precision=6) print('t, y, z') print(tabla) # GRAFICA #plt.plot(ti,yi, label='y(t)') plt.plot(ti,zi, color = 'Red', label='h(t)=dy/dt') plt.ylabel('dy/dt') plt.xlabel('t') plt.title('Respuesta impulso: Runge-Kutta 2do Orden d2y/dx2 ') plt.legend() plt.grid() plt.show()
Recuerde que se aplican las modificaciones de acuerdo al planteamiento del problema, por lo que revise los conceptos antes de aplicar el algoritmo.
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]