Referencia: Lathi 2.3 p163, Ejemplo 2.4 p159, Oppenheim problema 2.2.2 p97, Hsu 2.5.E p61
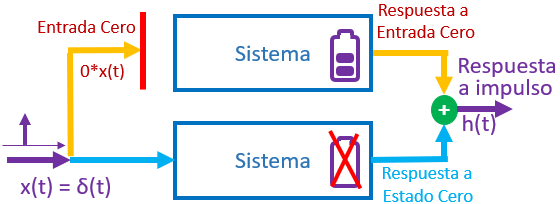
La respuesta de un sistema al impulso h(t), se obtiene al aplicar un impulso unitario δ(t) en la entrada x(t), semejante a un destello durante un tiempo muy pequeño.

El impulso es semejante a tomar una foto con flash en una habitación oscura, con todo tranquilo, sin movimientos. Luego del flash, a pesar que ya no exista más la luz, todos las personas o seres vivos reaccionan al destello de luz durante un tiempo y visualizaron el contenido de la habitación, ésta es la respuesta al impulso del sistema.
La respuesta del sistema se puede conformar como la suma de una señal contínua generada mediante una secuencia de impulsos cuando el tiempo entre impulsos tiende a cero (dt→0).
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
| ZSR = h(t) ⊗ x(t) |
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]
1. Respuesta a impulso h(t): Desarrollo Analítico
Un sistema de orden 2 se describe con la expresión de operadores D como:
Q(D)y(t) = P(D) x(t) (a_0 D^2+a_1 D + a_2)y(t)=(b_0 D^2 + b_1 D + b_2) x (t)para disminuir la cantidad de variables se hace a0=1, al dividir la ecuación en ambos lados para a0. El resultado como aún tiene variables desconocidas, se mantiene la nomenclatura, que de forma simplificada se presenta como:
( D^2+a_1 D + a_2)y(t)=(b_0 D^2 + b_1 D + b_2) x (t)La respuesta de un sistema al impulso unitario δ(t) aplicada en t=0, con todas las condiciones iniciales en cero en t=0-, se conoce como h(t).
(D^2+a_1 D + a_2)h(t)=(b_0 D^2 + b_1 D + b_2) \delta (t)Para el análisis se consideran dos intervalos:
– Para t≥0+ donde x(t)=0, cuya respuesta es conocida como los términos de modos característicos o respuesta homogenea desarrollada en respuesta entrada cero ZIR
(D^2+a_1 D + a_2)h(t)=0, t \ge 0
h(t) = términos de modos característicos
– Para t=0 donde existe x(t)=δ(t), que suma a la respuesta anterior una constante A0 por un impulso.
h(t) = (términos de modos característicos) + A0 δ(t)
que al insertar esta ecuación en la expresión original tenemos:
(D^2+a_1 D + a_2)(A_0 \delta(t) + \text{terminos modos caracteristicos}) = =(b_0 D^2 + b_1 D + b_2) \delta (t)que al multiplicar la parte de la izquierda, y comparando términos de ambos lados se determina que A0 = b0
que es como expresar
h(t) = b_0 \delta (t) + \text{modos caracteristicos}y si el orden del lado derecho M es menor que el del izquierdo N, b0=0.
h(t)=b_0 \delta (t)+ [P(D)y_n (t)] \mu (t)Revisar Lathi 2.3 pdf 163 para una descripción más detallada del método.
Método simplificado al emparejar impulsos
Referencia: Lathi 2.3 p165
El método permite reducir el procedimiento para determinar h(t) de un sistema LTIC.
h(t) = b_0 \delta (t) + [P(D) y_n(t)] \mu (t)donde yn(t) es una combinación de modos característicos del sistema sujeto a las condiciones iniciales siguientes:
y_n(0) = y'_n(0) = y''_n(0) = y_n^{(N-2)}(0) = 0 y_n^{(N-1)}(0) = 1Donde y(k)n(0) es el valor de la k-ésima derivada de yn(t) para t=0.
Si orden de P(D) es menor que el orden de Q(D) entonces b0=0 y el término del impulso b0δ(t) en h(t) es cero.
| N = 1 | yn(0) = 1 |
| N = 2 | yn(0) = 0, y’n(0) = 1 |
| N = 3 | yn(0) = 0, y’n(0) = 0, y"n(0) = 1 |
| N = 4 | … |
Ejemplo 1. Respuesta al impulso de una ecuación diferencial lineal de 2do orden
Referencia: Lathi Ejemplo 2.6 p166, Oppenheim 2.2.2 p94
Un sistema se describe con la ecuación mostrada y se pide determinar la respuesta al impulso unitario h(t).
( D^2 + 3D +2 ) y(t) = Dx(t) ( D^2 + 3D +2 ) y(t) = (D+0)x(t)Desarrollo Analítico
Semejante al análisis realizado para respuesta a entrada cero ZIR, el problema tiene un sistema se segundo orden con polinomio característico:
\lambda ^2 + 3\lambda +2 = (\lambda +1)(\lambda + 2)| Raíces características | Modos característicos |
| λ1 = -1 | e-t |
| λ2 = -2 | e-2t |
con lo que la solución general tienen la forma:
y_0 (t) = c_1 e^{-t} + c_2 e^{-2t}se toman las condiciones iniciales de la tabla del método simplificado para emparejar impulsos para N=2, por ser un sistema de segundo orden
y(0) = 0 , y'(0) = 1
y se aplican en la solución general:
y_0 (t) = c_1 e^{-t} + c_2 e^{-2t} y'_0 (t)= -c_1 e^{-t} -2c_2 e^{-2t}al sustituir los valores iniciales en la solución general con t=0, se obtienen los valores de las constantes,
0 = c1 + c2 1 = -c1 - 2c2 c1 = 1 c2 = -1
obteniendo como solución de la ecuación homogenea:
y_n (t) = 1 e^{-t} - 1e^{-2t}De la ecuación del problema, se tiene que del lado derecho de la ecuación, P(D)=D, entonces:
P(D)y_n (t) = Dy_n (t) = y'_n (t) = -e^{-t} + 2e^{-2t}Dado el caso que en la ecuacion, el orden de la derivadas de la derecha M es menor que el orden de derivadas de la izquierda N, (N>M), el término de segundo orden no se encuentra en P(D), entonces: b0=0
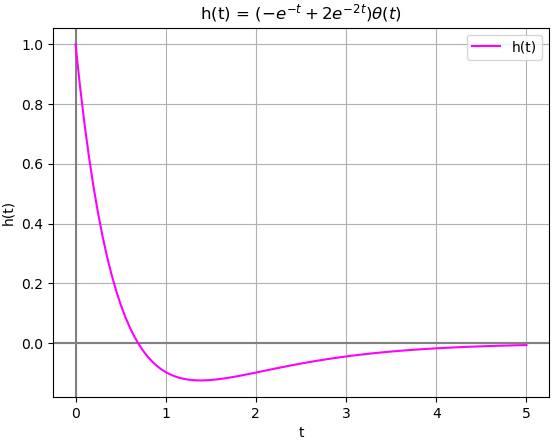
h(t) = b_0 \delta (t) + [P(D) y_n(t)] \mu (t) h(t)= 0\delta (t) + [-e^{-t} + 2e^{-2t}] \mu (t) h(t)= (-e^{-t} + 2e^{-2t})\mu (t)Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]