Ejercicio: 1Eva2016TII_T4 LTI DT Sistema 2do orden
literal a. Ecuación de diferencias de coeficientes constantes
Al diagrama del ejercicio se añaden las referencias de y[n], y[n-1] y y[n-2] de acuerdo a los bloques de retraso (delay) para escribir la expresión: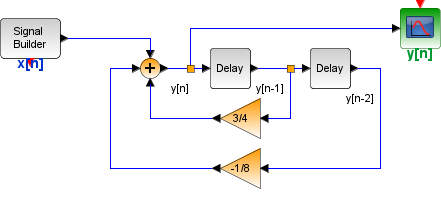
Para usar los operadores ‘E’ y encontrar el polinomio característico, dado que el sistema es LTI – DT, se puede desplazar 2 unidades:
y[n+2] - \frac{3}{4} y[n+1] + \frac{1}{8} y[n] = x[n+2]La expresión usando notación de operadores ‘E’ es:
\Big[ E^2 - \frac{3}{4} E + \frac{1}{8} \Big] y[n] = E^2 x[n]donde el numerador P[E] = E2
y el denominador Q[E] = E2 – (3/4)E +(1/8)
literal b. Respuesta a impulso
A partir de la notación de operadores’E’, se busca los modos característicos en el polinomio del denominador Q(E). También se expresa como y[n] como resultado de entrada cero x[n]=0
Q[E] = E^2 - \frac{3}{4} E + \frac{1}{8} \gamma^2 - \frac{3}{4} \gamma + \frac{1}{8} = 0usando la fórmula o el algoritmo se busca las raices del polinomio Q(E):
(\gamma - \frac{1}{4})(\gamma - \frac{1}{2}) = 0 \gamma_1 = \frac{1}{4} ; \gamma_2 = \frac{1}{2}Siendo raices reales y no repetidas, la respuesta del sistema tiene la forma:
y_c[n] = c_1 \Big( \frac{1}{4} \Big) ^n +c_2 \Big( \frac{1}{2} \Big) ^nse convierte a la forma:
h[n] =\frac{b_n}{a_n} \delta [n] + y_c[n] \mu [n] h[n] = \Bigg[ c_1 \Big( \frac{1}{4} \Big) ^n +c_2 \Big( \frac{1}{2} \Big) ^n \Bigg] \mu [n]Para encontrar los coeficientes c1 y c2, se requieren dos valores iniciales. En el literal a se indica que el sistema es causal, en consecuencia «No es posible obtener una salida antes que se aplique la entrada» y tenemos que: y[-1] = 0; y[-2] = 0.
La ecuación original de y[n] para respuesta a impulso tiene entrada x[n]=δ[t]
y[n] = \frac{3}{4} y[n-1] - \frac{1}{8} y[n-2] + x[n] y[n] = \frac{3}{4} y[n-1] - \frac{1}{8} y[n-2] + \delta [n]donde el impulso tiene valor de 1 solo en n=0, haciendo equivalente h[n] equivale a y[n] , entonces:
h[n] = \delta [n] + \frac{3}{4} h[n-1] - \frac{1}{8} h[n-2]n = 0
h[0] = \delta [0] + \frac{3}{4} h[-1] - \frac{1}{8} h[-2] h[0] = \delta [0] + \frac{3}{4} (0) - \frac{1}{8} (0) = 1n=1
h[1] = \delta [1] + \frac{3}{4} h[0] - \frac{1}{8} h[-1] h[1] = (0) + \frac{3}{4} (1) - \frac{1}{8} (0) = \frac{3}{4}con lo que es posible encontrar c1 y c2,
h[0] = 1 = c_1 \Big( \frac{1}{4} \Big) ^0 \mu [0] + c_2 \Big( \frac{1}{2} \Big) ^0 \mu (0) c_1 + c_2 = 1 h[1] = \frac{3}{4} = c_1 \Big( \frac{1}{4} \Big) ^1 \mu [1] + c_2 \Big( \frac{1}{2} \Big) ^1 \mu (1) \frac{1}{4} c_1 + \frac{1}{2} c_2 = \frac{3}{4}resolviendo:
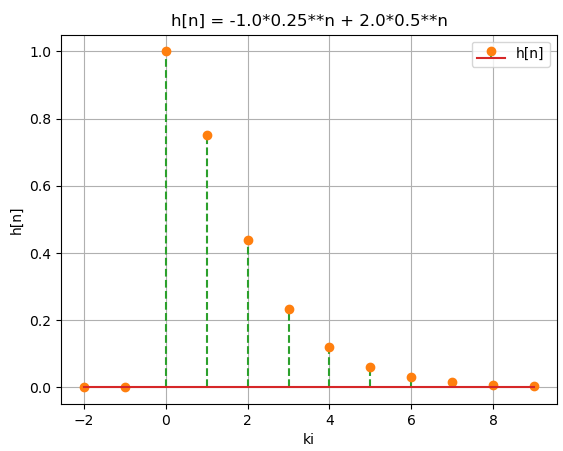
c_1 = -1 c_2 = 2 h[n] = - \Big( \frac{1}{4} \Big) ^n \mu [n] + 2 \Big( \frac{1}{2} \Big) ^n \mu [n] h[n] = \Bigg[ 2 \Big( \frac{1}{2} \Big) ^n - \Big( \frac{1}{4} \Big) ^n \Bigg] \mu [n]Observaciones:
Las raíces características o frecuencias naturales del sistema se encuentran dentro del círculo de radio unitario. El sistema es asintóticamente estable, que implica que es BIBO estable.
h[n] no es de la forma k δ[n], por lo que el sistema global es con memoria.
La forma de respuesta al impulso se vuelve evidente que el sistema es IIR.
Algoritmo en Python
Usando el algoritmo de LTID – Respuesta impulso. Ejercicio con Python:
respuesta impulso:
hi: [1. 0.75]
Matriz:
[[1. 1. ]
[0.5 0.25]]
Ch: [ 2. -1.]
n>=0, hn:
n n
- 0.25 + 2.0*0.5
>>>
Instrucciones Python
# Sistema LTID. Respuesta impulso # QE con raices Reales NO repetidas Lathi ejemplo 3.13 pdf271 # Lathi ejemplo 3.18 y 3.19 pdf278, # blog.espol.edu.ec/telg1001 import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO # coeficientes E con grado descendente QE = [1.0, -3/4, 1/8] PE = [1., 0., 0.] # condiciones iniciales ascendente ...,y[-2],y[-1] inicial = [0, 0.] tolera = 1e-6 # casi_cero muestras = 10 # para grafica # PROCEDIMIENTO # Respuesta a ENTRADA CERO # raices, revisa numeros complejos gamma = np.roots(QE) revisaImag = np.iscomplex(gamma) escomplejo = np.sum(revisaImag) # coeficientes de ecuacion m_q = len(QE)-1 Ac = np.zeros(shape=(m_q,m_q),dtype=float) # revisa si parte compleja <tolera o casi_cero if escomplejo>0: for i in range(0,m_q,1): valorimag = np.imag(gamma[i]) if np.abs(valorimag)<tolera: gamma[i] = float(np.real(gamma[i])) sumaj = np.sum(np.abs(np.imag(gamma))) if sumaj <tolera: print(sumaj) gamma = np.real(gamma) escomplejo = 0 # revisa repetidos unicoscuenta = np.unique(gamma,return_counts=True) repetidas = np.sum(unicoscuenta[1]-1) # Respuesta impulso h[n] ki = np.arange(-m_q,m_q,1) hi = np.zeros(m_q, dtype=float) xi = np.zeros(2*m_q, dtype=float) xi[m_q] = 1 # impulso en n=0 Ah = np.zeros(shape=(m_q,m_q),dtype=float) # h[n] iterativo p_n = len(PE) for i in range(0,m_q,1): for k in range(m_q,2*m_q,1): hi[i] = hi[i] - QE[k-m_q]*hi[m_q-k+1] for k in range(0,p_n,1): hi[i] = hi[i] + PE[k]*xi[m_q+i] Bh = np.copy(hi[:m_q]) # coeficientes de ecuacion for i in range(0,m_q,1): for j in range(0,m_q,1): Ah[i,j] = gamma[j]**(i) ch = np.linalg.solve(Ah,Bh) # ecuacion hn n = sym.Symbol('n') hn = 0*n for i in range(0,m_q,1): hn = hn + ch[i]*(gamma[i]**n) # SALIDA if escomplejo == 0: print('\n respuesta impulso: ') print('Bh:',Bh) print('Matriz: ') print(Ah) print('Ch: ',ch) print('n>=0, hn: ') sym.pprint(hn) else: print(' existen raices con números complejos.') print(' usar algoritmo de la sección correspondiente.') # grafica datos ki = np.arange(-m_q,muestras,1) hi = np.zeros(muestras+m_q) if escomplejo == 0: # evaluación de h[n] h_n = sym.lambdify(n,hn) hi[m_q:] = h_n(ki[m_q:]) # grafica h[n] plt.stem(ki,hi,label='h[n]', markerfmt ='C1o', linefmt='C2--') plt.legend() plt.grid() plt.ylabel('h[n]') plt.xlabel('ki') plt.title('h[n] = '+str(hn)) plt.show()
literal c. respuesta de paso s[n]
s[n] = \sum_{k=-\infty}^{n} h[k] s[n \rightarrow \infty] = \sum_{k=-\infty}^{\infty} h[k] = \sum_{k=-\infty}^{\infty} \Bigg[ 2 \Big( \frac{1}{2} \Big) ^k - \Big( \frac{1}{4} \Big) ^k \Bigg] \mu [k] = \sum_{k=0}^{\infty} \Bigg[ 2 \Big( \frac{1}{2} \Big) ^k - \Big( \frac{1}{4} \Big) ^k \Bigg]considerando que:
\sum_{k=0}^{\infty} \alpha ^k = \frac{1}{1-\alpha} ; |\alpha|<1se reemplaza con:
s[n \rightarrow \infty] = \sum_{k=0}^{\infty} \Bigg[ 2 \Big( \frac{1}{2} \Big) ^k - \Big( \frac{1}{4} \Big) ^k \Bigg] = 2\frac{1}{1-\frac{1}{2}} - \frac{1}{1-\frac{1}{4}} = 2(2) - \frac{4}{3} s[n \rightarrow \infty] =\frac{8}{3}un método mas detallado es:
s[n] = \sum_{k=-\infty}^{n} h[k] s[n] = \sum_{k=-\infty}^{n} \Bigg[ 2 \Big( \frac{1}{2} \Big) ^k - \Big( \frac{1}{4} \Big) ^k \Bigg] \mu [k] s[n] = \sum_{k=0}^{n} \Bigg[ 2 \Big( \frac{1}{2} \Big) ^k - \Big( \frac{1}{4} \Big) ^k \Bigg] s[n] = 2 \sum_{k=0}^{n} \Big( \frac{1}{2} \Big) ^k - \sum_{k=0}^{n} \Big( \frac{1}{4} \Big) ^kconsiderando que:
\sum_{k=0}^{n} \alpha ^k = \frac{1-\alpha ^{n+1}}{1-\alpha}se tiene lo siguiente,
s[n] = 2 \frac{1-\frac{1}{2}^{n+1}}{1-\frac{1}{2}} - \frac{1-\frac{1}{4}^{n+1}}{1-\frac{1}{4}} s[n] = 2 \frac{1-\frac{1}{2} \Big(\frac{1}{2} \Big)^{n}}{\frac{1}{2}} - \frac{1-\frac{1}{4} \Big( \frac{1}{4} \Big)^{n}}{\frac{3}{4}} s[n] = 4 \Bigg[ 1-\frac{1}{2} \Big(\frac{1}{2}\Big)^{n} \Bigg]- \frac{4}{3} \Bigg[ 1- \frac{1}{4} \Big(\frac{1}{4} \Big)^{n} \Bigg] s[n] = 4-2 \Big(\frac{1}{2}\Big)^{n} -\frac{4}{3}+ \frac{1}{3} \Big(\frac{1}{4} \Big)^{n} lim _ {n \to \infty}s[n] = lim _ {n \to \infty} \Bigg[ \frac{8}{3}-2 \Big(\frac{1}{2}\Big)^{n} + \frac{1}{3} \Big(\frac{1}{4} \Big)^{n} \Bigg] lim _ {n \to \infty}s[n] = \frac{8}{3}que es el mismo resultado que con el método presentado al inicio del literal.
Solución alterna: Usando transformada z
Revisar: LTID Transformada z – X[z] Fracciones parciales modificadas con Python
A partir de la ecuación de diferencias:
y[n+2] - \frac{3}{4} y[n+1] + \frac{1}{8} y[n] = x[n+2]en transformada z (unidad 7), que es semejante a operador ‘E’,
z^2 Y[z]- \frac{3}{4} z Y[z] + \frac{1}{8}Y[z] = z^2 X[z] \Big[ z^2 - \frac{3}{4} z + \frac{1}{8}\Big] Y[z] = z^2 X[z]la función de transferencia o respuesta al impulso se expresa como:
H[z] = \frac{X[z]}{Y[z]} = \frac{z^2}{z^2 - \frac{3}{4} z + \frac{1}{8}}usandolas raices del polinomio Q(E)
H[z] = \frac{z^2}{(z - \frac{1}{4})(z - \frac{1}{2})}para facilitar las operaciones se usan fracciones parciales modificadas,
\frac{H[z]}{z} = \frac{z}{(z - \frac{1}{4})(z - \frac{1}{2})} = \frac{k_1}{z - \frac{1}{4}} + \frac{k_2}{z - \frac{1}{2}}Usando el método de «cubrir» de Heaviside:
k_1 = \frac{z}{\cancel{(z - \frac{1}{4})}(z - \frac{1}{2})} \Big|_{z=1/4} = \frac{1/4}{1/4 - \frac{1}{2}} = -1 k_2 = \frac{z}{(z - \frac{1}{4})\cancel{(z - \frac{1}{2})}} \Big|_{z=1/2} = \frac{1/2}{1/2 - \frac{1}{4}} = 2reemplazando k1, k2 y restaurando a fracciones parciales al multiplicar ambos lados por z,
H[z] = \frac{-z}{z - \frac{1}{4}} + \frac{2z}{z - \frac{1}{2}}se puede usar la tabla de transformadas z para obtener el mismo resultado que el desarrolo anterior con operador ‘E’
h[n] = - \Big( \frac{1}{4} \Big) ^n \mu [n] + 2 \Big( \frac{1}{2} \Big) ^n \mu [n]