Ejercicio: 2Eva2009TII_T2 LTI DT Dado h[n], y[n] determine X[n]
literal a. Expresión de x[n]
Con los datos de h[n] y y[n], se obtienen las transformadas H[z] y Y[z],
h[n] = 2 \Big( \frac{1}{3} \Big)^n \mu [n-1] = 2 \Big( \frac{1}{3} \Big)^1\Big( \frac{1}{3} \Big)^{-1}\Big( \frac{1}{3} \Big)^n \mu [n-1] h[n] = \frac{2}{3} \Big( \frac{1}{3} \Big)^{n-1} \mu [n-1]la transformada z es:
H[z] = \frac{2}{3} \frac{1}{z-\frac{1}{3}}Para la señal de salida Yc[z] conocida:
y_c[n] = (-2)^{n} \mu [n-1] = (-2)^1(-2)^{n-1} \mu [n-1] y_c[n] = -2 (-2)^{n-1} \mu [n-1]la transformada z es:
Y_c[z] = -2\frac{1}{z+2}La señal de entrada x[n]
x[n] = a\delta [n] + b (c)^{n-1} \mu [n-1] X[z] = a + b \frac{1}{z-c}La señal de salida Y[z] esperada en dominio z se obtiene como Y[z] = H[z]X[z], la expresión se escribe como:
y_e [z] = \Bigg[\frac{2}{3} \frac{1}{z-\frac{1}{3}}\Bigg] \Bigg[a + b \frac{1}{z-c}\Bigg] = \frac{2}{3} \Bigg[\frac{a}{z-\frac{1}{3}} + \frac{b}{(z-c)(z-\frac{1}{3})}\Bigg] = \frac{2}{3} \Bigg[\frac{a(z-c) + b}{(z-c)(z-\frac{1}{3})}\Bigg] y_e [z] = \frac{2}{3} \Bigg[\frac{a(z-c) + b}{(z-c)(z-\frac{1}{3})}\Bigg] = \frac{2}{3} \Bigg[\frac{az - ac + b}{(z-c)(z-\frac{1}{3})}\Bigg]igualando las expresiones con Y[z] conocida con Y[z] esperada:
Y_c[z] = Y_e[z] -2\frac{1}{z+2} = \frac{2}{3} \Bigg[ \frac{az - ac + b}{(z-c)(z-\frac{1}{3})} \Bigg] -3\frac{1}{z+2} = \frac{az - ac + b}{(z-c)(z-\frac{1}{3})}para que el denominador quede (z+2), se iguala el término con (z-c), con lo que c=-2
-3\frac{1}{z+2} = \frac{az-a(-2) + b}{(z+2)(z-\frac{1}{3})} -3 = \frac{az+2a + b}{(z-\frac{1}{3})} -3 (z-\frac{1}{3}) = az +2a + b -3 z + 1 = az + 2a + bcomparando el término z, se tiene que a=-3, quedando solo la parte constante para determinar el valor de b
2a + b = 1 2(-3) + b = 1se tiene que b= 7
teniendo la expresión de la entrada como:
x[n] = -3\delta [n] + 7 (-2)^{n-1} \mu [n-1]literal b. Ecuacion de diferencias H[z]
Se inicia con los datos de H[z]
H[z] = \frac{X[z]}{Y[z]} = \frac{2}{3} \frac{1}{z-\frac{1}{3}} \Big(z-\frac{1}{3} \Big) Y[z] = \frac{2}{3}X[z] zY[z]-\frac{1}{3} Y[z] = \frac{2}{3}X[z] y[n+1]-\frac{1}{3} y[n] = \frac{2}{3}x[n]literal c. Diagrama de bloques
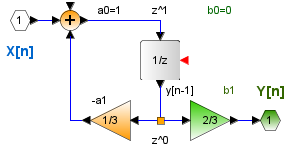
Para el diagrama de bloques se desplaza para despejar y[n]
y[n]-\frac{1}{3} y[n-1] = \frac{2}{3}x[n-1] y[n]= \frac{1}{3} y[n-1] + \frac{2}{3}x[n-1] H[z] = \frac{X[z]}{Y[z]} = \frac{2}{3} \frac{1}{z-\frac{1}{3}}Observaciones:
Las raíces características o frecuencias naturales del sistema H[z] se encuentran dentro del círculo de radio unitario. El sistema es asintóticamente estable, que implica que es BIBO estable.