Referencia: Lathi 1.3.2 p78, Hsu 1.2.B p2
1. Señales Analógicas
Una señal se clasifica como analógica cuando su amplitud puede tomar un infinito numero de valores en un rango contínuo de tiempo.
Por ejemplo, una señal de sonido como la del archivo:
Nota: Descargue el archivo use un programa como windows media player para escuchar su contenido.
Instrucciones en Python
Para observar en una gráfica la señal del archivo de sonido anterior, a las librerías numéricas y gráficas, se añade la librería SciPy (scientific Python) que dispone de instrucciones para lecturas de archivos de audio en formato .wav
Nota: Si usa WinPython la librería viene incluida, en otro caso se puede instalar con PIP install scipy en la línea de comandos del sistema.
En el algoritmo se define el nombre del archivo.wav a usar, y mediante la instrucción waves.read() se obtienen los datos de velocidad de muestreo y el arreglo de sonido.
# Señales analógicas import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves # INGRESO # archivo = input('archivo de audio: ') archivo = 'Alarm01.wav' muestreo, sonido = waves.read(archivo) # SALIDA - Observacion intermedia print('frecuencia de muestreo: ', muestreo) print('dimensiones de matriz: ', np.shape(sonido)) print('datos de sonido: ') print(sonido)
el resultado del algoritmo muestra:
frecuencia de muestreo: 22050 dimensiones de matriz: (122868, 2) datos de sonido: [[0 0] [0 0] [0 0] ..., [0 0] [0 0] [0 0]]
En caso de requerir revisar más detalles sobre audio.wav se pueden encontrar en el siguiente enlace.
Archivos de Audio.wav – Abrir, extraer una porción
Con los resultados mostrados, se observa que:
- la señal de audio tiene frecuencia de muestreo de 22050 Hz
- Las dimensiones de la matriz sonido (122868,2) indican que es de tipo estéreo por usar dos columnas,
- el valor de 122868 corresponde a la cantidad de muestras por canal,
- Los índices para seleccionar un canal son 0 ó 1 interpretado como canal izquierdo o derecho.
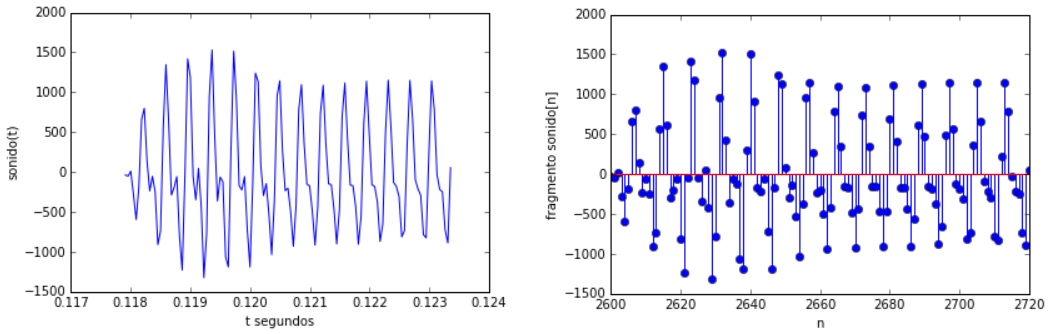
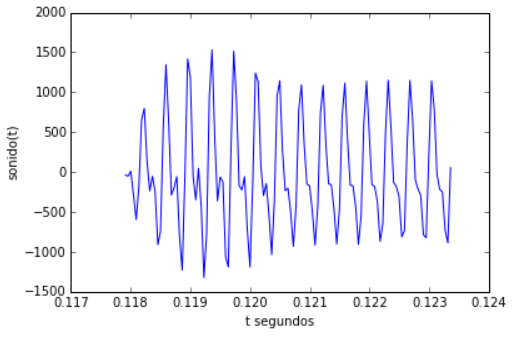
Para observar la forma del sonido se extrae el canal 0 y solo un segmento o intervalo de tiempo [inicia,termina).
Para observar otros segmentos la señal de audio cambie los valores de [inicia,termina), añadiendo las instrucciones siguientes:
# segmento de tiempo canal = 0 inicia = 2600 termina = 2720 # Extrae el segmento desde sonido dt = 1/muestreo ti = np.arange(inicia*dt,termina*dt,dt) muestras = len(ti) segmento = sonido[inicia:inicia+muestras, canal] #SALIDA plt.plot(ti,segmento) plt.xlabel('t segundos') plt.ylabel('sonido(t)') plt.show()
2. Señales Digitales
Una señal se clasifica como digital cuando la amplitud puede tomar solo un número finito de valores, para un número finito de muestras en el tiempo.
Siguiendo el ejemplo de la señal de audio, las señales digitales se las asocia con computadoras. Para almacenar una señal de audio, se la cuantifica en amplitud a espacios iguales de tiempo dt.
Por ejemplo, datos del vector segmento del audio del ejercicio anterior muestran el caracter finito, discreto, por muestras de la señal.
# SALIDA - datos del segmento de audio print(segmento)
[ -36 -52 11 -280 -595 -186 656 800 141
-237 -53 -246 -910 -739 569 1347 620 -288
-195 -57 -812 -1229 -37 1419 1183 -51 -348
47 -424 -1322 -778 955 1531 432 -363 -62
-123 -1062 -1189 306 1514 910 -172 -224 -57
-720 -1191 -164 1241 1134 75 -295 -144 -533
-1035 -367 953 1144 262 -234 -202 -499 -931
-423 781 1095 344 -152 -174 -491 -916 -440
739 1088 353 -149 -158 -467 -901 -472 693
1116 405 -164 -172 -434 -906 -558 608 1139
478 -159 -181 -370 -870 -655 494 1151 565
-130 -180 -307 -812 -735 358 1149 666 -95
-213 -291 -785 -824 214 1143 784 -31 -217
-249 -727 -888 54]
los datos del segmento de audio, muestran que la señal de audio se almacena como una señal discreta, o digital, por lo que una gráfica más apropiada es:
# grafica segmento de sonido en forma discreta ni = np.arange(inicia,inicia+muestras,1) plt.stem(ni,segmento) plt.xlabel('n') plt.ylabel('segmento sonido[n]') plt.show()
Observaciones
Los términos «contínuo en el tiempo» y «discreto en el tiempo» cuantifican la naturaleza de la señal solo en el eje de las abscisas (horizontal).
Los términos «analógicos» y «digitales» cuantifican la amplitud de la señal o eje de las ordenadas (vertical).
Una señal de audio, por su naturaleza es de tipo analógica, que para almacenarla o procesarla en un computador se convierte a digital al cuantificar sus valores de amplitud, de la forma mostrada en el ejercicio.
Tarea
- cambie los rangos de observación de la señal de audio y repita las gráficas para su forma analógica aproximada (parte 1) y para su forma digital (parte 2)
- comente sobre el segmento al inicio y final de todo el audio donde los valores de la señal son 0’s
Instrucciones en Python
# Señales analógicas import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves # INGRESO archivo = 'Alarm01.wav' # segmento de tiempo canal = 0 inicia = 2600 termina = 2720 # PROCEDIMIENTO muestreo, sonido = waves.read(archivo) # Extraer el segmento de sonido dt = 1/muestreo ti = np.arange(inicia*dt, termina*dt , dt) muestras = len(ti) segmento = sonido[inicia: inicia+muestras,canal] # SALIDA print('frecuencia de muestreo:', muestreo) print('dimensiones de sonido: ',np.shape(sonido)) print('datos del sonido:') print(sonido) print('segmento:') print(segmento) # Grafica plt.stem(ti,segmento) plt.xlabel('t segundos') plt.ylabel('sonido(t)') plt.show()