Señal Periódica
Referencia: Oppenheim 1.2.2 p11, Hsu Cap1.2,F p4, Lathi 1.3.3. p79
Una señal periódica contínua tiene la propiedad que su valor se repite luego de un desplazamiento de tiempo T. El valor de T es conocido como el «periodo de la señal» que es el tiempo en el que se vuelve a repetir la forma de onda a partir de un punto de referencia.
x(t) = x(t+T)La relación entre el periodo T y la frecuencia f se da por la ecuación:
f = \frac{1}{T} \text{, en Hz} \omega = 2 \pi f = \frac{2 \pi}{T} \text{, en rad/s}otra forma de escribir la ecuación es:
x(t) = x(t + mT)para cualquier valor de t y cualquier número entero m. El periodo fundamental T0 de x(t) es el valor positivo más pequeño que hace posible la ecuación descrita.
Instrucciones en Python
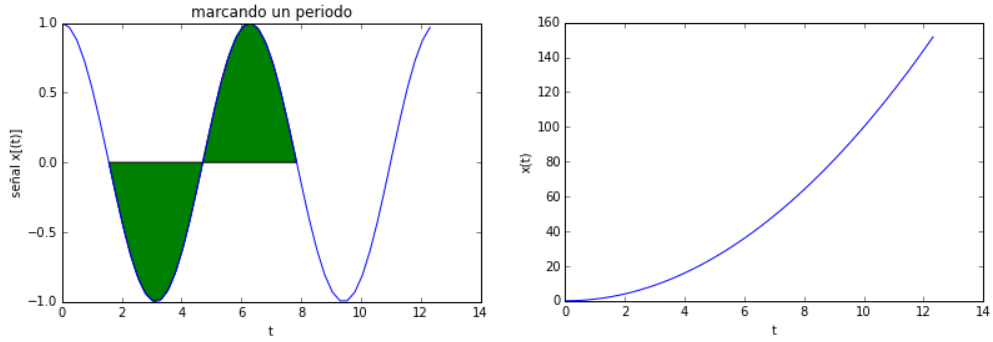
Las instrucciones son semejantes a graficar señales contínuas. Para el ejemplo se analiza la señal coseno(t), con periodo T=2π para un en un intervalo de dos periodos m=2 y 51 muestras. Se crea el vector ti para el intervalo de observación y se calcula la señal.
# Señales periodicas import numpy as np import matplotlib.pyplot as plt # INGRESO T = 2*np.pi f = 1/T w = 2*np.pi*f fx = lambda t: np.cos(w*t) t0 = 0 # intervalo tiempo [t0,tn] m = 2 # incluir m periodos en grafica muestras = 51 desde = T/4 # marcar periodo [desde,hasta] # PROCEDIMIENTO tn = m*T # vector de tiempo ti = np.linspace(t0,tn,muestras) # dt = ti[1]-ti[0] dt = (tn-t0)/(muestras-1) senal = fx(ti) # marcar un periodo en [desde, hasta] hasta = desde + T + dt tperiodo = np.arange(desde,hasta,dt) periodo = fx(tperiodo)
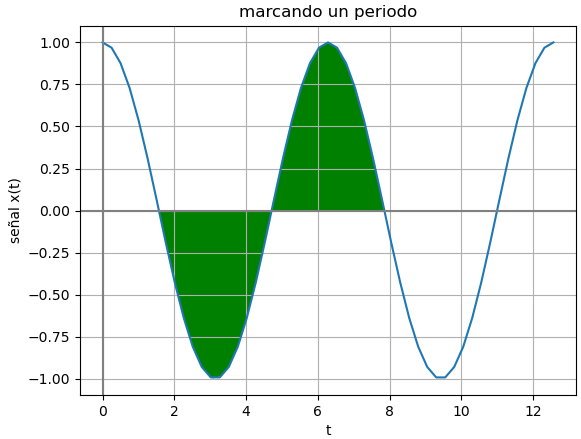
La gráfica se conforma de dos partes:
- la señal calculada
- la señal marcada en un periodo
# SALIDA # Grafica plt.plot(ti,senal) plt.xlabel('t') plt.ylabel('señal x(t)') plt.grid() plt.axhline(0, color='gray') plt.axvline(0, color='gray') # marcar un periodo plt.title('marcando un periodo') plt.fill_between(tperiodo,0, periodo,facecolor='green') plt.show()
Señal periódica discreta
Se define semejante a las señales periódicas contínuas como una secuencia discreta en el tiempo x[n]. La señal es periódica con periodo N si existe un número entero positivo para el que:
x[n + N] = x[n] \text{, para todo n} x[n + mN] = x[n]para todo n y cualquier entero m
El periodo fundamental N0 de x[n] es el valor positivo mas pequeño para que se cumpla la ecuación en la secuencia de datos de la señal.
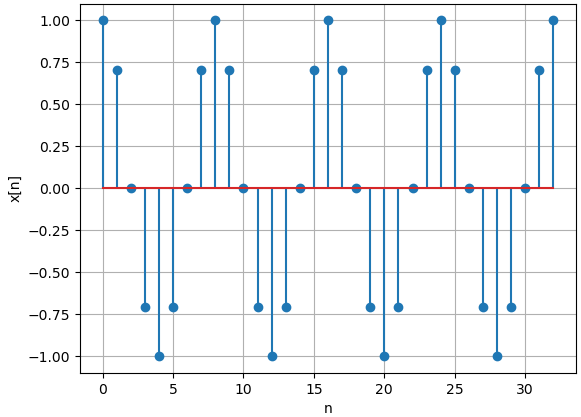
Como ejemplo se usa una señal muestreada del coseno:
Instrucciones en Python
Semejante al algoritmo del ejercicio anterior, se genera la nueva gráfica en forma discreta.
# Señales periodicas Discretas import numpy as np import matplotlib.pyplot as plt # INGRESO parametros N = 8 w = 2*np.pi/N fx = lambda n: np.cos(w*n) n0 = 0 # intervalo [n0,n0+muestras] m = 4 # incluir m periodos en grafica # PROCEDIMIENTO muestras = m*N+1 ni = np.arange(n0,n0+muestras,1) senal = fx(ni) # SALIDA # Grafica plt.stem(ni,senal) plt.xlabel('n') plt.ylabel('x[n]') plt.grid() plt.show()
Señal No periódica o Aperiódica
En éste caso, los valores de la señal x(t) no se repiten para ningún valor de T.
También para algunos problemas se considera que T → ∞.
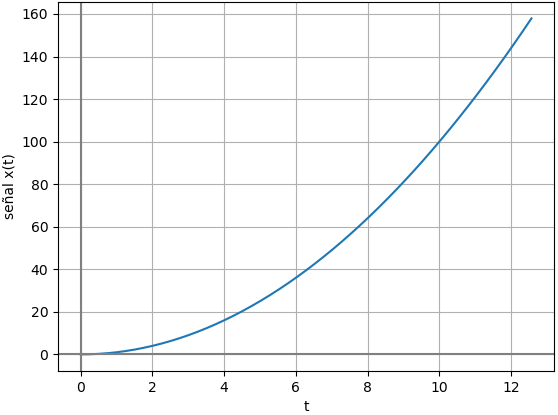
Un ejemplo del tipo de señal es: x(t)=t^2
Instrucciones en Python
Usando lo realizado para señales periódicas contínuas, cambiando la función fx y quitando las marcas de un periodo.
# Señales NO periodicas contínuas import numpy as np import matplotlib.pyplot as plt # INGRESO T = 2*np.pi f = 1/T w = 2*np.pi*f fx = lambda t: t**2 t0 = 0 # intervalo tiempo [t0,tn] m = 2 # incluir m periodos en grafica muestras = 51 # PROCEDIMIENTO tn = m*T # vector de tiempo ti = np.linspace(t0,tn,muestras) senal = fx(ti) # SALIDA # Grafica plt.plot(ti,senal) plt.xlabel('t') plt.ylabel('señal x(t)') plt.grid() plt.axhline(0, color='gray') plt.axvline(0, color='gray') plt.show()
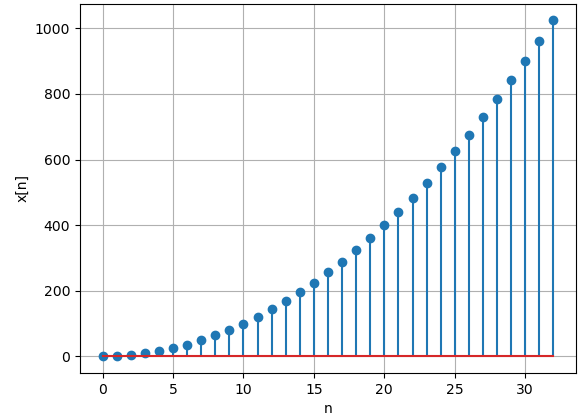
Para el caso de señal discreta, considere el punto de partida del algoritmo correspondiente y modifique:
yn = lambda n: n**2 # SALIDA - Gráfica plt.stem(ni,yi) plt.xlabel('n') plt.ylabel('y[n]') plt.show()
Tarea
Pruebe con otras funciones contínuas para x(t) como:
- t^3
- e^t
- \frac{1}{t}
en Python, el exponente se escribe como: t**3 y en la otra función np.exp(t)
Realizar el mismo paso para sus formas discretas.