Referencia: Lathi 1.8 p111, Schaum/Hsu 2.5.B p60, Oppenheim 2.56.d p160, p700
La descripción de un sistema en términos de las mediciones en los extremos se denomina Modelo de entrada-salida.
Una forma es describir la relación entre salida/entrada se expresa usando operadores de diferenciación D:
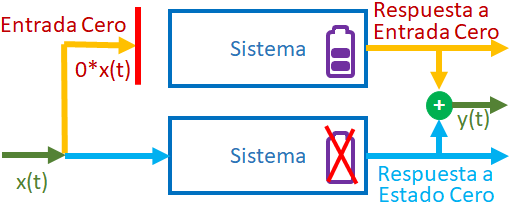
\frac{y(t)}{x(t)} = \frac{P(D)}{Q(D)}La respuesta de un sistema lineal puede también ser expresada como la suma de dos componentes: respuesta a entrada cero ZIR y respuesta a estado cero ZSR.
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
Para el caso de un circuito eléctrico RLC, el modelo inicia con la descripción de la ecuación diferencial lineal que relaciona el voltaje x(t) de entrada y la corriente de salida y(t).
Ejemplo 1. Corriente en circuito RLC y Ecuaciones Diferenciales Lineales de 2do orden
Referencia: Lathi 1.8-1 p111. Oppenheim problema 2.61c p164 Ejemplo 9.24 p700
Para el ejemplo, se plantea determinar la corriente de lazo y(t) del circuito mostrado en la imagen. 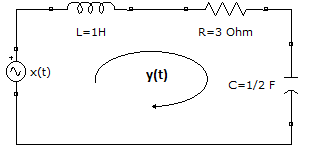
Usando la ley de voltajes en lazo se tiene que:
vL(t) + vR(t) +vC(t) = x(t)
que con las leyes de corriente para cada elemento (inductor, resistor y capacitor) se traducen en la ecuación integro-diferencial:
\frac{dy(t)}{dt} +3 y(t) + 2\int_{-\infty}^t y(\tau)d\tau = x(t)Para tener todo expresado con un solo operador, se derivan ambos lados de la ecuación:
\frac{d^{2}y(t)}{dt^{2}} + 3\frac{dy(t)}{dt} + 2y(t) = \frac{dx(t)}{dt}que es la relación de "entrada-salida" del sistema con la entrada x(t) y la salida y(t) que permitirá analizar el sistema que representa al circuito.
Notación D para derivadas y 1/D para integrales
Por conveniencia, para usar una notación más compacta de la ecuación diferencial, el operador dy/dt se cambia por la notación D.
\frac{d}{dt}y(t) = Dy(t) \frac{d^2}{dt^2} y(t) = D^{2}y(t)Que convierte la ecuación de entrada-salida a la expresión:
(D^2 + 3D +2)y(t) = Dx(t)que es identica a la expresión de entrada y salida que describe al circuito.
El operador diferencial D también se interpreta con la notación para integrales,
\int_{-\infty}^t y(\tau)d\tau = \frac{1}{D}y(t)por lo que la expresión integro-diferencial del circuito,
\frac{d}{dt}y(t) +3 y(t) + 2\int_{-\infty}^t y(\tau)d\tau = x(t)también se puede escribir en notación D como:
D y(t) + 3 y(t)+ \frac{2}{D} y(t) = x(t)Al multiplicar ambos lados por el operador D se convierte nuevamente en una expresión sin denominadores D, semejante a la expresión que usa solo diferenciales.
\Big( D^2 + 3D + 2 \Big) y(t) = D x(t)Recuerde: la expresión con operadores D, NO ES una ecuación algebraica, pues la expresión de operadores D aplican solo a y(t).
En adelante, para el sistema o circuito descrito por ecuaciones diferenciales se usa el operador D=\frac{d}{dt}, por ejemplo:
a_2 \frac{d^2}{dt^2}y(t) + a_1 \frac{d}{dt}y(t) + a_0 y(t) = b_1\frac{d}{dt}x(t) + b_0x(t) a_2 D^ 2y(t) + a_1 Dy(t) + a_0y(t) = b_1Dx(t) + b_0 x(t) (a_2 D^ 2 + a_1 D + a_0)y(t) = (b_1D + b_0 )x(t)las expresiones de los operadores D de cada lado se conocen también como P(D) y Q(D)
Q(D) y(t) = P(D) x(t) P(D) = b_1D + b_0 Q(D) = a_2 D^ 2 + a_1 D + a_0La relación de salida/entrada del sistema se expresa como:
\frac{y(t)}{x(t)} = \frac{b_1D + b_0}{a_2 D^ 2 + a_1 D + a_0}Ejercicio 2. Voltaje de un Circuito RC como una Ecuación Diferencial Lineal de 1er Orden
Referencia: Lathi Ejemplo 1.17 p113.
Usando la notación del operador D, encuentre la relación de salida/entrada para el circuito RC. Para ésto defina i(t) como la corriente del circuito y como y(t) el voltaje del capacitor.
La corriente del lazo i(t) del circuito:
R i(t) +\frac{1}{C} \int_{-\infty}^{t} i(\tau) \delta \tau = x(t)cambiando al operador D
R i(t) +\frac{1}{C} \frac{1}{D} i(t) = x(t) R D i(t) +\frac{1}{C} i(t) = D x(t) \Big(R D +\frac{1}{C}\Big) i(t) = D x(t)Conociendo que la corriente i(t) en el capacitor depende de la variación de voltaje y(t) y la capacitancia C
i(t) = C \frac{\delta}{\delta t} y(t) = CD y(t)se sustituye i(t) en la ecuación,
(R D +\frac{1}{C}) CD y(t) = D x(t)simplificando un operador D
(R D +\frac{1}{C}) C y(t) = x(t) (RC D + 1 ) y(t) = x(t)Para mostrar la relación de salida/entrada se reordena la expresión:
\frac{y(t)}{x(t)} = \frac{1}{RC D +1} \frac{y(t)}{x(t)} = \frac{\frac{1}{RC}}{D +\frac{1}{RC}}Expresando con P(D) y Q(D)
Q(D) y(t) = P(D) x(t) P(D) = \frac{1}{RC} Q(D) = D +\frac{1}{RC}Formas de encontrar una solución
Se pueden plantear varias formas de desarrollo para la solución de la ecuación diferencial lineal, usando los conceptos analíticos y numéricos:
1. Desarrollo analítico, que es el tradicional con papel y lápiz.
2. Desarrollo usando algoritmos en Python:
2.1 desarrollo analítico con fórmulas simbólicas en Sympy-Python
2.2 desarrollo numérico con funciones en Scipy-Python para LTI
2.3 desarrollo numérico con Runge-Kutta d2y/dx2 para EDO del curso Métodos Numéricos.
3. Desarrollo usando un simulador con:
3.1 usando diagrama de bloques
3.2 usando un diagrama de circuito
Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python] [Runge-Kutta d2y/dx2] [Simulador]