Referencia: Lathi 4.1. p330. Hsu 3.2.A p110, Oppenheim 9.1 p655
La transformada de Laplace permite simplificar el proceso de solución de ecuaciones integro-diferenciales usando operaciones mas simples al cambiar desde el dominio del tiempo 't' al dominio 's'.
Para una señal contínua x(t), la transformada de Laplace esta definida como:
X(s) = \int_{-\infty}^{\infty} x(t) e^{-st} dtPara el caso de señales contínuas, lineales y causales, se define una señal x(t) que tiene un componente escalón unitario μ(t), por lo que la integral se desarrolla de forma unilateral. Se enfatiza que se entiende como transformada de Laplace unilateral si cada señal x(t) es cero para t<0, y es apropiado indicarlo al multiplicar la señal por el escalón unitario μ(t)
X(s) = \int_{-\infty}^{\infty} x(t) \mu(t) e^{-st} dt = \int_{0}^{\infty} x(t) \mu(t) e^{-st} dt
Para la transformada de Laplace unilateral, existe una transformada inversa de X(s) que es única. En consecuencia, no hay necesidad de especificar la región de convergencia (ROC) de forma explícita. Motivo por el que generalmente no se menciona la ROC para transformadas unilaterales. (Lathi p337).
La señal x(t) es la inversa de la transformada X(s), que se obtiene de la forma:
x(t) = \frac{1}{2πj} \int_{c-j\infty}^{c+j\infty} X(s) e^{st} dtdonde c es una constante seleccionada para asegurar la convergencia de la integral.
Los pares de ecuaciones conocidos como "Pares de la transformada de Laplace" se escriben de forma simbólica:
X(s) \Rightarrow \mathscr{L}[x(t)] x(t) \Rightarrow \mathscr{L}^{-1}[X(s)]que tienen algunas propiedades de interés para señales y sistemas como la linealidad,
\mathscr{L}[a_1 x_1(t) + a_2 x_2 (t)] = a_1 X_1(s) + a_2 X_2 (s)Para el desarrollo de ejercicios se usa principalmente la tabla de pares de Transformadas de Laplace, los pares se obtienen al aplicar la definición del integral. El desarrollo el integral se puede también realizar usando Sympy-Python.
Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]
..
Ejemplo 1. Integral de la Transformada de Laplace de una exponencial decreciente, un solo termino
Referencia: Lathi ejemplo 4.1. p331, Oppenheim Ejemplo 9.2 p656, Hsu Ejemplo 3.1 p111
Para una señal x(t) = e-atμ(t), encuentre la transformada X(s) y su región de convergencia (ROC)
x(t) = e^{-at} μ(t) X(s) = \int_{-\infty}^{\infty} e^{-at} \mu (t) e^{-st} \delta tpero tomando en cuenta que μ(t)=0 para t<0 y μ(t)=1 para t≥0:
X(s) = \int_{0}^{\infty} e^{-at} e^{-st} \delta t = \int_{0}^{\infty} e^{-(s+a)t} \delta t = -\frac{1}{s+a} e^{-(s+a)t}\Big|_{0}^{\infty} = \Big[-\frac{1}{s+a} e^{-(s+a)(\infty)}\Big]-\Big[ -\frac{1}{s+a} e^{-(s+a)(0)}\Big] X(s) = \frac{1}{s+a}con polo s=-a al producir división para cero en la expresión.
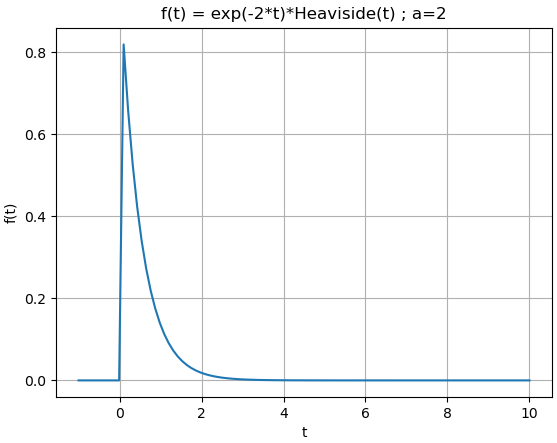
Se puede observar que la región de convergencia, ROC, de X(s) es Re(s)>-a, como se muestra en la gráfica. Para otros valores de s el integral no converge.
Para el ejemplo, siendo a=2
El siguiente video presenta una interpretación gráfica y animada de la transformada de Laplace en el plano s real e imaginario.
Propiedades de la transformada de Laplace
Otra de las propiedades de interés es la diferenciación. Por ejemplo, los sistemas formados por circuitos electrónicos que tienen inductores L, usan la variación de corriente o derivada de la corriente, generando ecuaciones diferenciales ordinarias. La transformada de Laplace presenta una alternativa viable para tratar estos circuitos como se mostrará en los ejemplos de la Unidad.
Propiedad de diferenciación
\frac{\delta x}{\delta t} \Leftrightarrow sX(s) - x(0^{-}) \frac{d^2x}{dt^2} \Leftrightarrow s^2X(s) - sx(0^{-}) - x'(0^{-}) \frac{\delta^3x}{\delta t^3} \Leftrightarrow s^3 X(s) - s^2 x(0^{-}) - sx'(0^{-}) - x''(0^{-})Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]
Ejemplo 2. Transformada de Laplace con suma de exponenciales
Referencia: Oppenheim Ejemplo 9.3 p658
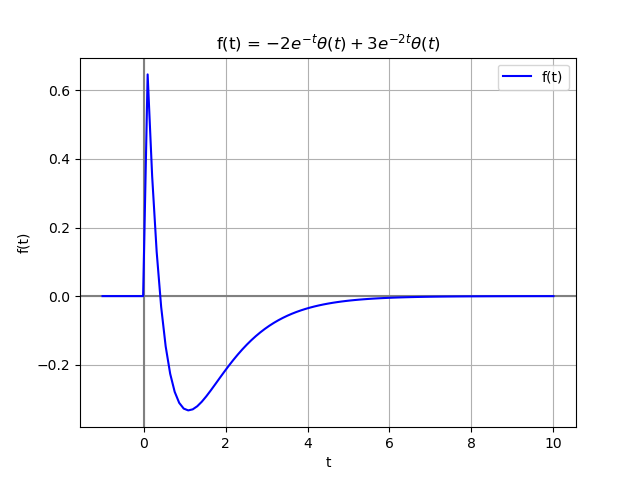
Considere la señal que es la suma de dos exponenciales:
x(t) = 3 e^{-2t}\mu (t) - 2e^{-t}\mu (t)se tiene que:
X(s) = \int_{0}^{\infty} \Big[ 3 e^{-2t} \mu (t) - 2e^{-t} \mu (t) \Big] e^{-st} \delta t X(s) = \int_{0}^{\infty} \Big[ 3 e^{-2t}e^{-st}\mu (t) - 2e^{-t}e^{-st}\mu (t) \Big] \delta t X(s) = \int_{0}^{\infty} \Big[ 3 e^{-(s+2)t}\mu (t) - 2e^{-(s+1)t} \mu (t) \Big] \delta tEn general para tratar este tipo de ejercicios es mejor descomponer la señal o función matemática en varios componentes de suma, siguiendo la propiedad de linealidad de los sistemas.
X(s) = 3 \int_{0}^{\infty} e^{-(s+2)t}\mu (t) \delta t - 2 \int_{0}^{\infty} e^{-(s+1)t} \mu (t) \delta t X(s) = -3 \frac{1}{s+2}e^{-(s+2)t}\Big|_{0}^{\infty} + 2 \frac{1}{s+1}e^{-(s+1)t}\Big|_{0}^{\infty} X(s) = -3 \frac{1}{s+2}\Big( e^{-(s+2)(\infty)} - e^{-(s+2)(0)} \Big) + 2 \frac{1}{s+1} \Big( e^{-(s+1)(\infty)} - e^{-(s+1)(0)} \Big) X(s) = -3 \frac{1}{s+2} \Big( 0-1 \Big) + 2 \frac{1}{s+1} \Big( 0 - 1 \Big) X(s) = 3 \frac{1}{s+2} - 2 \frac{1}{s+1}con polos en s=-1 y s=-2 al producir división para cero en la expresión
Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]
..
Ejemplo 3. Transformada de Laplace para suma de términos f(t) con desplazamiento, o función "gate" o compuerta
Referencia: Lathi práctica 4.1.a p337
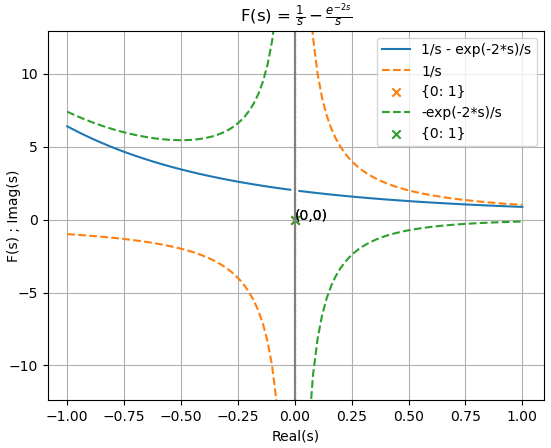
literal a. Por integración directa, encuentra la transformada X(s) y la región de convergencia para la función descrita en la imagen
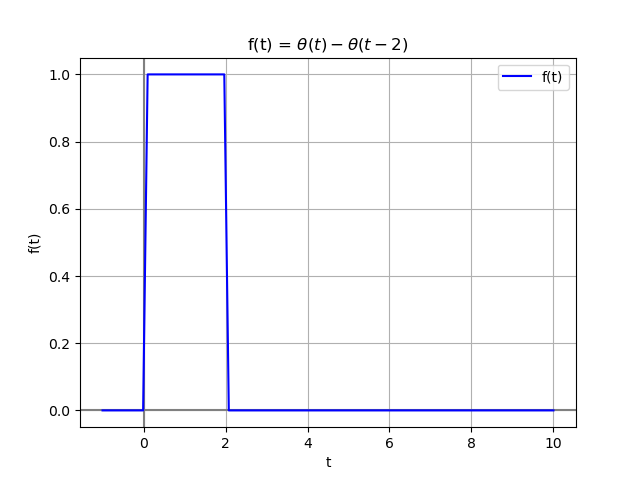
Analizando la expresión de la función es:
con polo en s=0
se observa también que el retraso de tiempo aplicado en μ(t-2) genera en la transformada un termino multiplicado por e(-2s).
Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]
..
Ejemplo 4. Transformada de Laplace para suma de términos f(t) con desplazamiento, función "gate" o compuerta causal
Referencia: Lathi práctica 4.1.b p337
literal b. Por integración directa, encuentra la transformada X(s) y la región de convergencia para la función descrita en la imagen
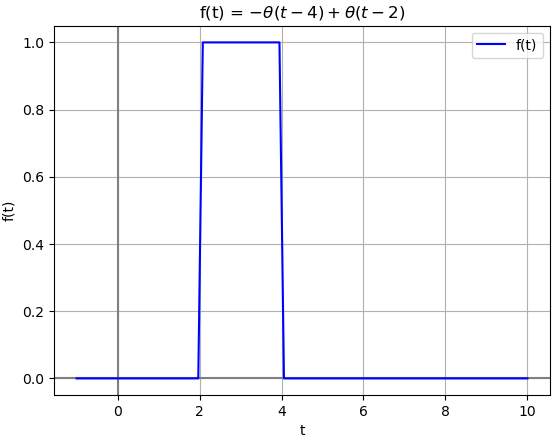
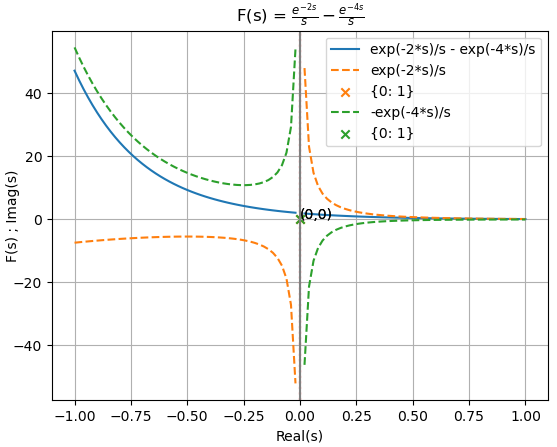
x(t) = \mu (t-2) - \mu (t-4)que observando el ejercicio anterior se puede deducir que los retrasos en cada término generan como resultado:
X(s) = \frac{1}{s} e^{-2s}-\frac{1}{s} e^{-4s}con polo en s=0
Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]
..
Ejemplo 5. Transformada de Laplace para cos(t)
Referencia: Oppenheim Ejemplo 9.4 p658
Para resolver el ejercicio de transformada de Laplace, observe que la expresión es un polinomio que se desarrolla de forma mas simple aplicando la tabla de transformadas.
x(t) = e^{-2t}\mu (t) + e^{-t} \cos (3t) \mu (t)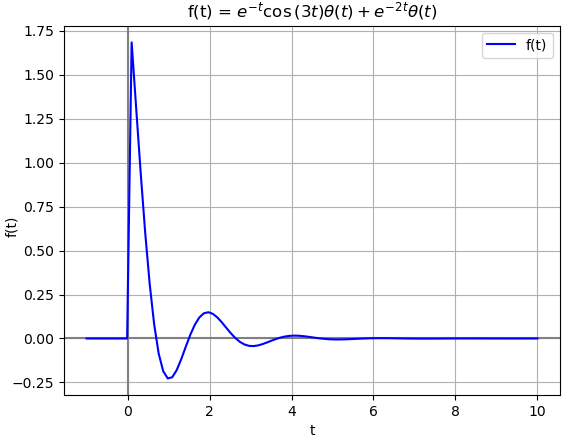
Usando el resultado del ejemplo 1 y la tabla de transformadas se tiene que:
agrupando términos en factores para obsevar mejor los polos
X(s) = \frac{2s^2+5s+12}{(s+2)(s^2 +2s+10)}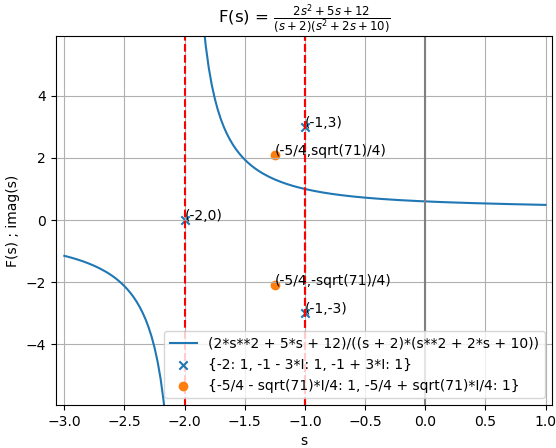
Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]
..
Ejercicio 6. Transformada de Laplace con impulso δ(t) y suma de exponenciales
Referencia: Oppenheim ejemplo 9.5 p661
El ejercicio propuesto contiene un componente de impulso unitario δ(t) aplicado en t=0. Se propone usar la tabla de transformadas de Laplace para resolverlo de forma directa, aunque se propone realizar el integral para comprobar el resultado.
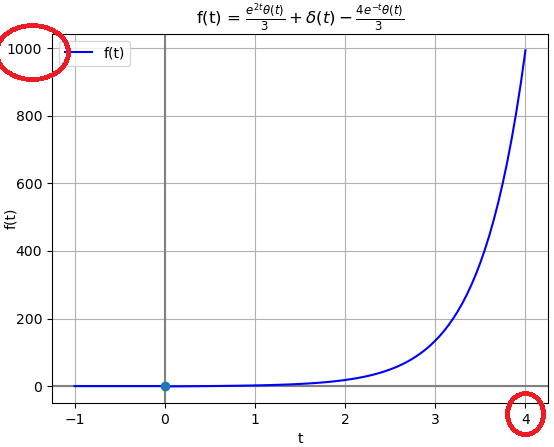
x(t) = \delta(t) -\frac{4}{3} e^{-t} \mu (t) + \frac{1}{3} e^{2t} \mu (t)Se tiene una función x(t) creciente en el tiempo y no acotada.
usando la tabla de transformadas se tiene que:
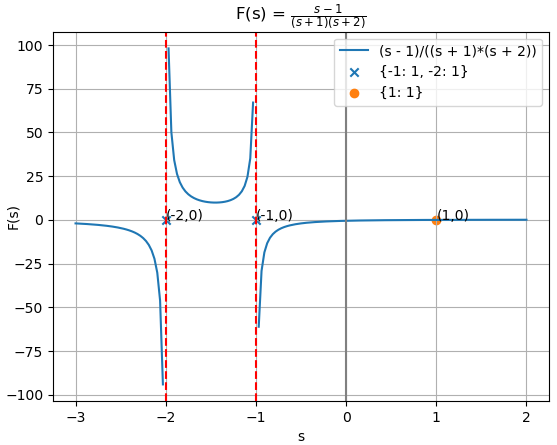
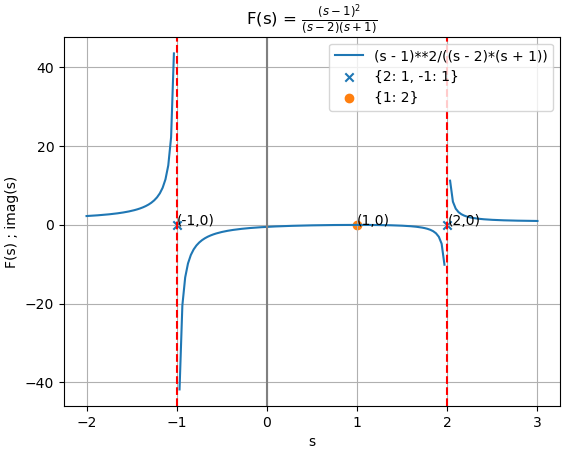
X(s) = 1 -\frac{4}{3} \frac{1}{s+1} + \frac{1}{3} \frac{1}{s-2}Para observar los polos y ceros se agrupa X(s) por factores
X(s) =\frac{(s-1)^2}{(s-2)(s+1)}la gráfica respecto al dominio s, mostrando los polos en s=2 y s=-1 que generan divisiones para cero. Observe que un polo se encuentra del lado derecho del plano, relacionado con el término creciente en el tiempo y no acotado.
Transformada de Laplace para: [ ej1 un Exponencial ] [ ej2 Suma de términos ] [ ej3 escalón Desplazado ] [ ej4 sumas desplazadas ] [ ej5 coseno ] [ ej6 impulso ]