[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
..
1. Producto de Señales
Un modelo de señal de gran utilidad es el producto de dos sinusoides, usada en difusión radial conocida como Modulación de Amplitud (AM).
[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
..
2. Ejemplo – Espectro de Producto de sinusoides
Referencia: McClellan ejemplo 3.2 p75
Realice el espectro de frecuencias para una señal resultado del producto de dos sinusoides con frecuencias 1/2 Hz y 5 Hz.
x(t) = \cos (\pi t) \sin(10 \pi t)[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
..
3. Desarrollo Analítico
Lo primero es convertir x(t) usando la fórmula de Euler:
x(t) = \Big( \frac{e^{j \pi t} +e^{-j \pi t}}{2} \Big)\Big( \frac{e^{j 10 \pi t} - e^{-j 10 \pi t}}{2j} \Big) = \frac{1}{4}e^{-j \pi /2}e^{j 11 \pi t} + \frac{1}{4}e^{-j \pi /2}e^{j 9 \pi t} + \frac{1}{4}e^{j \pi /2}e^{-j 9 \pi t} + \frac{1}{4}e^{j \pi /2}e^{-j 11 \pi t} = \frac{1}{2}\cos (11 \pi t - pi/2) +\frac{1}{2}\cos(9 \pi t - \pi/2)Se observa que para el espectro de frecuencias se tienen 4 componentes, que las frecuencias originales de 5 Hz y 1/2 Hz ya no se muestran en el espectro
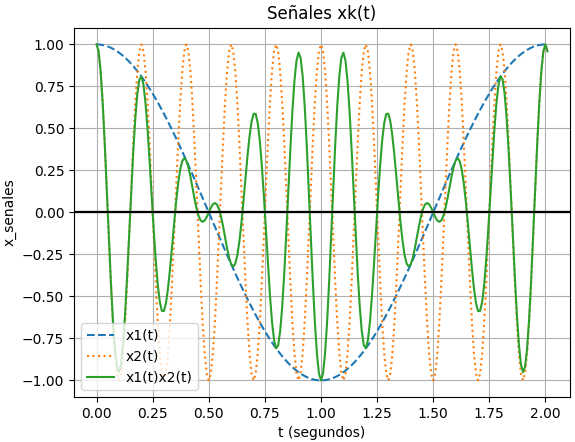
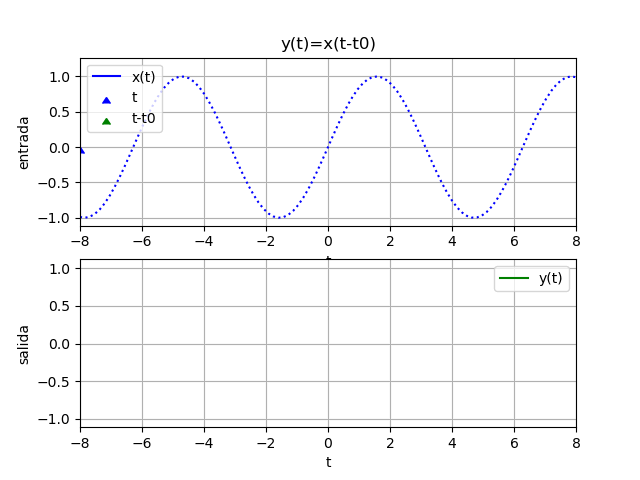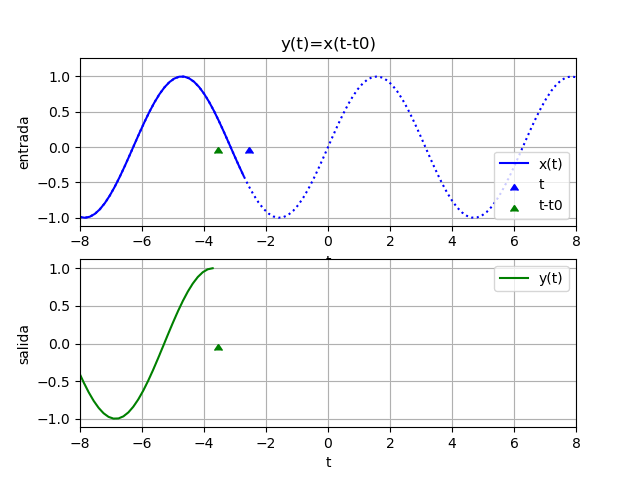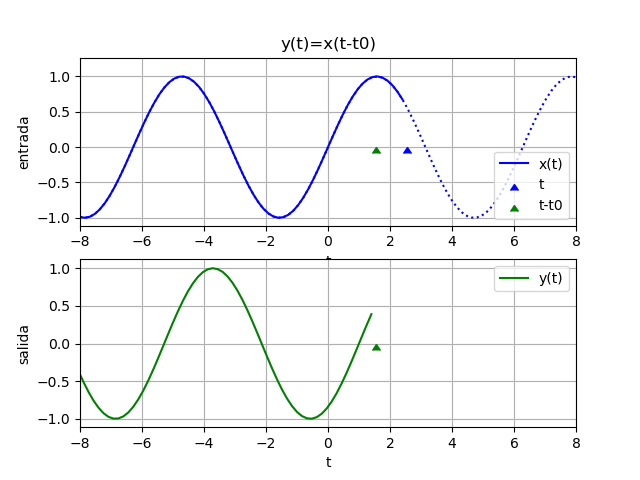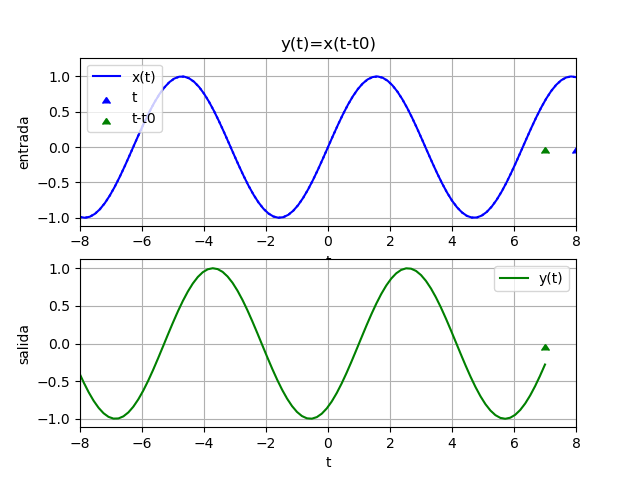
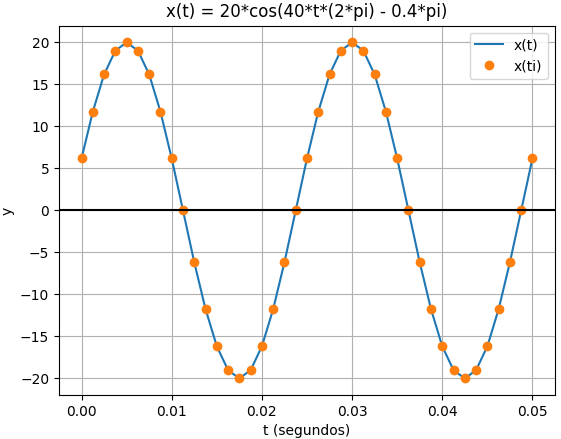
La gráfica de domino en tiempo con los componentes individuales es:
[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
..
4. Algoritmo en Python
El algoritmo para el ejercicio reutiliza las funciones descritas en la sección anterior para el espectro de frecuencias. Por lo que éste caso es una aplicación del concepto.
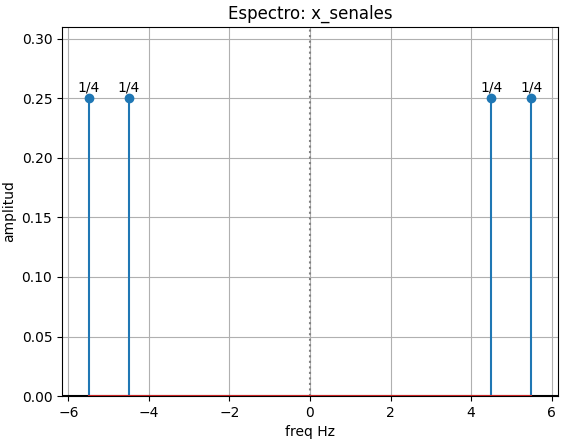
El resultado del algoritmo es:
x(t): cos(pi*t)*cos(10*pi*t) x_senales: senal: cos(pi*t)*cos(10*pi*t) euler: exp(11*I*pi*t)/4 + exp(9*I*pi*t)/4 + exp(-9*I*pi*t)/4 + exp(-11*I*pi*t)/4 x_simplif: cos(9*pi*t)/2 + cos(11*pi*t)/2 x_espectro: freq : [-5.5 -4.5 4.5 5.5] ampl : [1/4 1/4 1/4 1/4] fase : [0 0 0 0] etiq : ['1/4' '1/4' '1/4' '1/4']
Instrucciones e Python
# ejemplo 3.2 p75 Espectro de dos lados # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1034 as dsp # variables from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x0 = 0 x1 = sym.cos(pi*t) x2 = sym.cos(10*pi*t) x = x1*x2 # PROCEDIMIENTO x_senales = dsp.cos_x_components_add(x) x_conteo = len(x_senales) Xe_senales = dsp.cos_to_euler_one_term(x_senales) Xe_espectro = dsp.cos_spectrum_list(x_senales) # x_senales simplificados Xe_conteo = len(Xe_senales) x_senales_simple = [] x_simplif = sym.S.Zero for i in range(Xe_conteo): unaSenal = Xe_senales[i] Xe_to_cos = unaSenal.rewrite(sym.cos) x_simplif = x_simplif + Xe_to_cos # SALIDA print('x(t):',x) print('x_senales: ') for i in range(x_conteo): print('senal: ',x_senales[i]) print(' euler:',Xe_senales[i]) print('x_simplif: ') print(' ',x_simplif) print('x_espectro:') for unparam in Xe_espectro: print(unparam,':',Xe_espectro[unparam])
[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
..
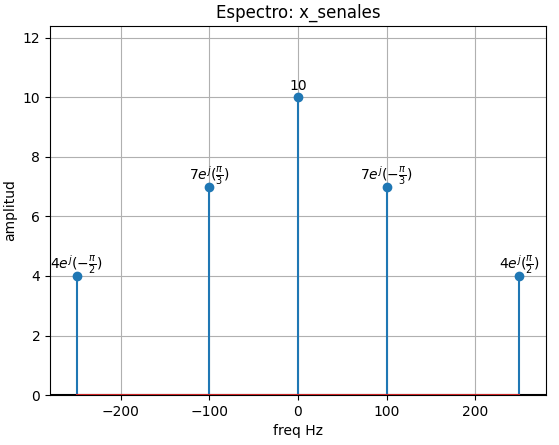
5. Gráfica de espectro de frecuencias
Instrucciones adicionales para la gráfica de espectro son las mismas que en la sección anterior
# GRAFICAS de espectro de frecuencias --------- freq = Xe_espectro['freq'] magnitud = Xe_espectro['ampl'] etiqueta = Xe_espectro['etiq'] mag_max = float(max(magnitud)) freq_max = float(max(freq)) # grafica graf_dx = 0.12 fig_espectro = plt.figure() graf_fasor = fig_espectro.add_subplot() # grafica magnitud graf_fasor.set_xlim([-freq_max*(1+graf_dx),freq_max*(1+graf_dx)]) graf_fasor.set_ylim([0,mag_max*(1+graf_dx*2)]) graf_fasor.axhline(0,color='black') graf_fasor.axvline(0,linestyle='dotted',color='grey') graf_fasor.stem(freq,magnitud) # etiquetas de fasor for k in range(0,len(freq),1): texto = etiqueta[k] x_text = freq[k] y_text = magnitud[k] plt.annotate(texto,xy=(x_text,y_text), xytext=(0,5), textcoords='offset points',ha='center') graf_fasor.grid() graf_fasor.set_xlabel('freq Hz') graf_fasor.set_ylabel('amplitud') graf_fasor.set_title('Espectro: x_senales') #plt.show()
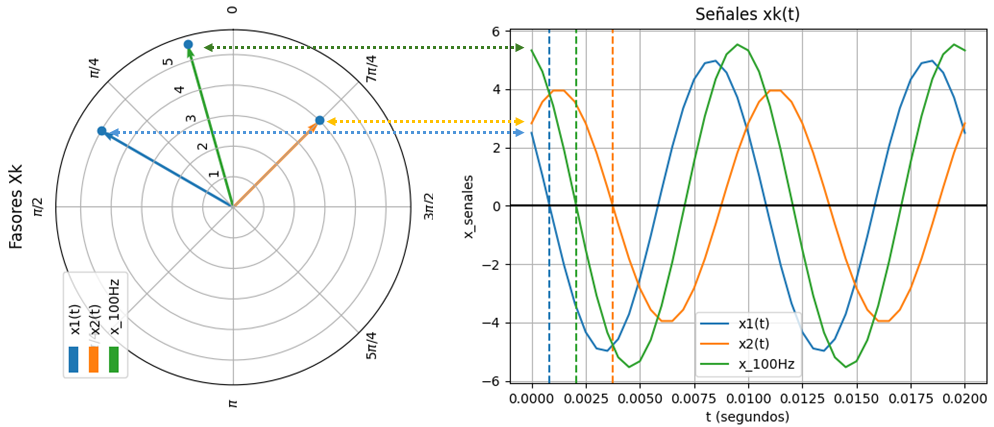
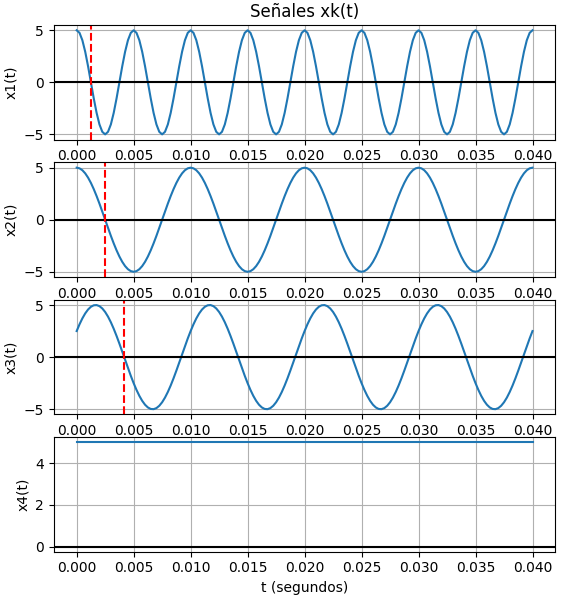
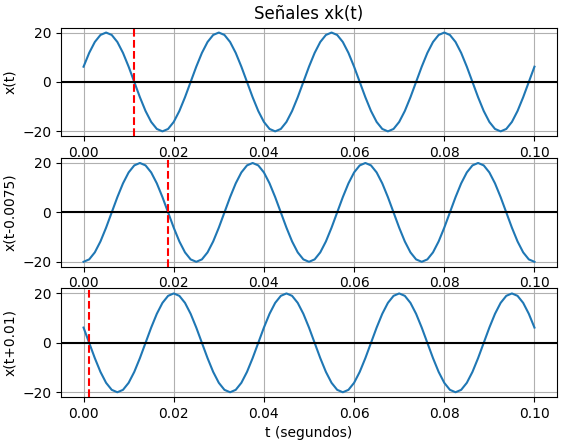
La gráfica de tiempo, permite observar el efecto del producto se señales.
Se reutilizan las instrucciones de la sección 1.3, añadiendo las variantes de estilo de línea para destacar la señal resultante del producto.
En este caso se está usando la lista de frecuencias del espectro de señales, lo que no incluye las frecuencias individuales de cada componente al desaparecer en el resultado las frecuencia originales. por lo que la «envolvente» de menor frecuencia no domina sobre las demás.
Considerar el caso presentado para completar el algoritmo si se requiere mayor precisión.
# GRAFICAR x(t) --------------------------- # INGRESO x_senales_graf = [x1,x2,x] # para graficar x_etiqueta = ['x1(t)','x2(t)','x1(t)x2(t)'] x_tipolinea = ['dashed','dotted','solid'] tramos_T = 20 # tramos por periodo periodos_graf = 2 # periodos en una grafica # PROCEDIMIENTO GRAFICA x_conteo_graf = len(x_senales_graf) # etiquetas si están vacias if len(x_etiqueta)==0: if x_conteo_graf > 1: for i in range(0,x_conteo_graf-1,1): x_etiqueta.append('x'+str(i)+'(t)') x_tipolinea.append('dotted') x_etiqueta.append('x(t)') x_tipolinea.append('solid') [T_min,T_max] = dsp.periodo_minmax(freq) x_conteo = len(x_senales_graf) muestras_T = tramos_T + 1 # intervalo de t entre [a,b] en pasos dt a = 0 b = T_max*periodos_graf dt = T_min/tramos_T # tamaño de paso,tramo, muestreo ti = np.arange(a,b+dt,dt) xi_k = [] # muestras de cada señal x for unasenal in x_senales_graf: # x(t) a forma numérica lambda t: if unasenal.has(t): xk = sym.lambdify(t,unasenal) else: # es constante xk = lambda t: unasenal + 0*t xki = xk(ti) # evalúa en intervalo xi_k.append(np.copy(xki)) # graficar fig_x = plt.figure() graf_x = fig_x.add_subplot() for i in range(0,x_conteo_graf,1): color_i = dsp._graf_lineacolor_i(i) graf_x.plot(ti,xi_k[i], color=color_i, linestyle=x_tipolinea[i], label=x_etiqueta[i]) graf_x.axhline(0,color='black') graf_x.set_title('Señales xk(t)') graf_x.set_xlabel('t (segundos)') graf_x.set_ylabel('x_senales') graf_x.grid() graf_x.legend() plt.show()
[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
..
6. Modulación de Amplitud y Ancho de Banda
En comunicación por radio difusión se conoce el término Modulación de amplitud AM (amplitude modulation). AM es el proceso de multiplicar una señal sinusoidal de alta frecuencia fc (portadora) con una señal de baja frecuencia como la voz o música (envolvente)
x(t) = envolvente (portadora)
x(t) = v(t) \cos ( 2 \pi f_c t)El concepto de ancho de banda se usa con la representación del espectro de frecuencias de la señal y destaca una de sus características. Para el caso de AM cuyo espectro tiene como frecuencia mas alta (fc + fΔ ) y referenciada a la frecuencia de la portadora fc , se considera importante el grupo de frecuencias positivas en el intervalo entre la mas alta y las mas baja conocidas como ancho de banda o BW (Bandwitdth) de la señal.
(f_c + f_{\Delta})-(f_c - f_{\Delta}) = 2f_{\Delta}6.1 Ejercicio
Referencia: McClellan ejemplo 3.4 p78 y ejercicio 3.3 p80
Realice el espectro de frecuencias para una señal AM con portadora cos(400πt) y envolvente (5+4cos(40 πt)).
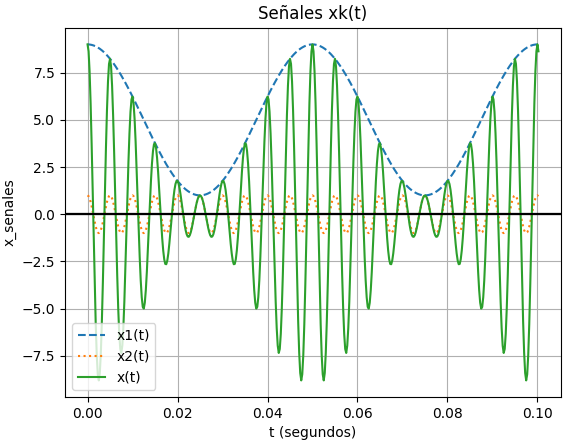
La señal envolvente tiene un término DC suficientemente grande que la mantiene en la parte superior (positiva) para todo ‘t’. El término DC de la envolvente permite simplificar la implementación de un circuito detector de envolvente en el radio-receptor, la envolvente es la voz o música que se quiere escuchar.
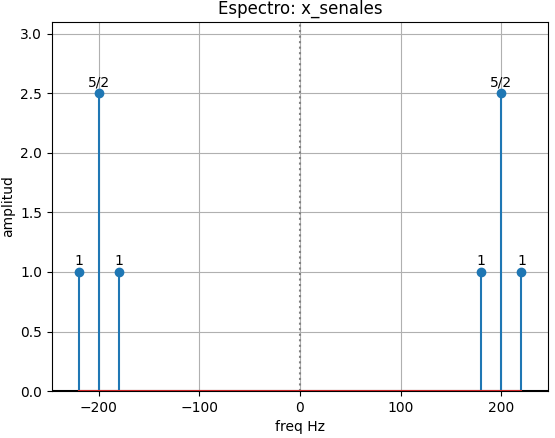
Obseve que la señal de la portadora es de 200Hz y la envolvente es 20Hz, con una relacion 1/10. En el espectro de frecuencia, la mas alta es 220 Hz y la mas baja es 180 Hz, la frecuencia central o portadora es 200 Hz. El ancho de banda es (220-180) = 40 Hz. que es la freciencia de la envolvente.
[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]
6.2 Algoritmo con Python
A partir del algoritmo del producto de señales, se añade el cálculo de las frecuencia máxima y mínima de x(t).
# ancho de banda freq = Xe_espectro['freq'] freq_max = float(max(freq)) freq_min = float(min(freq[freq>0])) # freq positivas [freq>0] freq_centro = (freq_max+freq_min)/2 BW = freq_max-freq_min
con lo que se obtiene como resultado
x(t): (4*cos(40*pi*t) + 5)*cos(400*pi*t) x_senales: senal: 5*cos(400*pi*t) euler: 5*exp(400*I*pi*t)/2 + 5*exp(-400*I*pi*t)/2 senal: 4*cos(40*pi*t)*cos(400*pi*t) euler: exp(440*I*pi*t) + exp(360*I*pi*t) + exp(-360*I*pi*t) + exp(-440*I*pi*t) x_simplif: 2*cos(360*pi*t) + 5*cos(400*pi*t) + 2*cos(440*pi*t) freq_min: 180.0 freq_centro: 200.0 freq_max: 220.0 ancho de banda BW: 40.0 x_espectro: freq : [-220. -200. -180. 180. 200. 220.] ampl : [1 5/2 1 1 5/2 1] fase : [0 0 0 0 0 0] etiq : ['1' '5/2' '1' '1' '5/2' '1']
con gráficas de espectro de frecuencia y x(t)
Algoritmo en Python con gráficas
# ejemplo 3.4 p78 Modulación de Amplitud (AM) o Amplitud Modulada # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1034 as dsp # variables from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x1 = 5+4*sym.cos(40*pi*t) x2 = sym.cos(400*pi*t) x = x1*x2 # PROCEDIMIENTO x_senales = dsp.cos_x_components_add(x) x_conteo = len(x_senales) Xe_senales = dsp.cos_to_euler_one_term(x_senales) Xe_espectro = dsp.cos_spectrum_list(x_senales) # x_senales simplificados Xe_conteo = len(Xe_senales) x_senales_simple = [] x_simplif = sym.S.Zero for i in range(Xe_conteo): unaSenal = Xe_senales[i] Xe_to_cos = unaSenal.rewrite(sym.cos) x_simplif = x_simplif + Xe_to_cos # ancho de banda freq = Xe_espectro['freq'] freq_max = float(max(freq)) freq_min = float(min(freq[freq>0])) # freq positivas [freq>0] freq_centro = (freq_max+freq_min)/2 BW = freq_max-freq_min # SALIDA print('x(t):',x) print('x_senales: ') for i in range(x_conteo): print('senal: ',x_senales[i]) print(' euler:',Xe_senales[i]) print('x_simplif: ') print(' ',x_simplif) print(' freq_min:',freq_min) print('freq_centro:',freq_centro) print(' freq_max:',freq_max) print('ancho de banda BW:',BW) print('x_espectro:') for unparam in Xe_espectro: print(unparam,':',Xe_espectro[unparam]) # GRAFICAS de espectro de frecuencias --------- freq = Xe_espectro['freq'] magnitud = Xe_espectro['ampl'] etiqueta = Xe_espectro['etiq'] mag_max = float(max(magnitud)) freq_max = float(max(freq)) # grafica graf_dx = 0.12 fig_espectro = plt.figure() graf_fasor = fig_espectro.add_subplot() # grafica magnitud graf_fasor.set_xlim([-freq_max*(1+graf_dx),freq_max*(1+graf_dx)]) graf_fasor.set_ylim([0,mag_max*(1+graf_dx*2)]) graf_fasor.axhline(0,color='black') graf_fasor.axvline(0,linestyle='dotted',color='grey') graf_fasor.stem(freq,magnitud) # etiquetas de fasor for k in range(0,len(freq),1): texto = etiqueta[k] x_text = freq[k] y_text = magnitud[k] plt.annotate(texto,xy=(x_text,y_text), xytext=(0,5), textcoords='offset points',ha='center') graf_fasor.grid() graf_fasor.set_xlabel('freq Hz') graf_fasor.set_ylabel('amplitud') graf_fasor.set_title('Espectro: x_senales') #plt.show() # GRAFICAR x(t) --------------------------- # INGRESO x_senales_graf = [x1,x2,x_simplif] # para graficar x_etiqueta = ['x1(t)','x2(t)','x(t)'] x_tipolinea = ['dashed','dotted','solid'] tramos_T = 20 # tramos por periodo periodos_graf = 4 # periodos en una grafica # PROCEDIMIENTO GRAFICA x_conteo_graf = len(x_senales_graf) # etiquetas si están vacias if len(x_etiqueta)==0: if x_conteo_graf > 1: for i in range(0,x_conteo_graf-1,1): x_etiqueta.append('x'+str(i)+'(t)') x_tipolinea.append('dotted') x_etiqueta.append('x(t)') x_tipolinea.append('solid') [T_min,T_max] = dsp.periodo_minmax(freq) x_conteo = len(x_senales_graf) muestras_T = tramos_T + 1 # intervalo de t entre [a,b] en pasos dt a = 0 b = T_max*periodos_graf dt = T_min/tramos_T # tamaño de paso,tramo, muestreo ti = np.arange(a,b+dt,dt) xi_k = [] # muestras de cada señal x for unasenal in x_senales_graf: # x(t) a forma numérica lambda t: if unasenal.has(t): xk = sym.lambdify(t,unasenal) else: # es constante xk = lambda t: unasenal + 0*t xki = xk(ti) # evalúa en intervalo xi_k.append(np.copy(xki)) # graficar fig_x = plt.figure() graf_x = fig_x.add_subplot() for i in range(0,x_conteo_graf,1): color_i = dsp._graf_lineacolor_i(i) graf_x.plot(ti,xi_k[i], color=color_i, linestyle=x_tipolinea[i], label=x_etiqueta[i]) graf_x.axhline(0,color='black') graf_x.set_title('Señales xk(t)') graf_x.set_xlabel('t (segundos)') graf_x.set_ylabel('x_senales') graf_x.grid() graf_x.legend() plt.show()
[ producto cos ] [ ejercicio ] [ analítico ] [ algoritmo ] [gráfica ] [ AM y BW]