s2Eva2017TII_T2 Volumen de isla

Ejercicio: 2Eva2017TII_T2 Volumen de isla

isla = np.array([[0,1,0,0,0],
                 [1,3,1,1,0],
                 [5,4,3,2,0],
                 [0,0,1,1,0]])

xi = np.array([0,100,200,300,400])
yi = np.array([0, 50,100,150])

Tamaño de la matriz: n=4, m=5

cantidad de elementos por fila impar, aplica Simpson 1/3
hx = (200-0)/2 =100
fila=0
    vector = [0,1,0,0,0]
    deltaA = (100/3)(0+4(1)+0) = 4(100/3)
    deltaA = (100/3)(0+4(0)+0) = 0
    area0 = 4(100/3) + 0 = 4(100/3)
fila=1
    vector = [1,3,1,1,0]
    deltaA = (100/3)(1+4(3)+1) = 14(100/3)
    deltaA = (100/3)(1+4(1)+0) = 5(100/3)
    area1 = 14(100/3) + 5(100/3) = 19(100/3)
fila=2
    vector = [5,4,3,2,0]
    deltaA = (100/3)(5+4(4)+3) = 24(100/3)
    deltaA = (100/3)(3+4(2)+0) = 11(100/3)
    area2 = 24(100/3) + 11(100/3) = 35(100/3)
fila=3
    vector = [0,0,1,1,0]
    deltaA = (100/3)(0+4(0)+1) = (100/3)
    deltaA = (100/3)(1+4(1)+0) = 5(100/3)
    area3 = (100/3) + 5(100/3) = 6(100/3)

areas = [ 4(100/3), 19(100/3), 35(100/3), 6(100/3)]
areas = (100/3)[ 4, 19, 35, 6 ]

areas tiene cantidad de elementos par, aplica Simpson 3/8
    hy = (150-0)/3 = 50
    deltaV = (3/8)(50)(100/3)(4+3(19) + 3(35)+ 6)
           = (25*25)(168)
    Volumen = 107500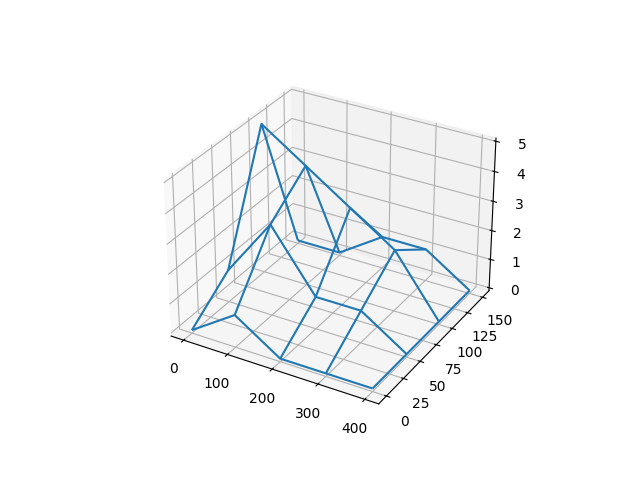

tramos:  4 5
areas:  [  133.33333333   633.33333333  1166.66666667    66.66666667]
Volumen:  107500.0

Instrucciones en Python para encontrar el valor son:

# 2da Eval II T 2017. Tema 2
# Formula de simpson
# Integración: Regla Simpson 1/3 y 3/8
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

def simpson13(xi,yi):
    '''
    las muestras deben ser impares
    '''
    area = 0
    muestras = len(xi)
    impar = muestras%2
    if impar == 1:
        for i in range(0,muestras-2,2):
            h = (xi[i+2] - xi[i])/2
            deltaA = (h/3)*(yi[i]+4*yi[i+1]+yi[i+2])
            area = area + deltaA
    return(area)

def simpson38(xi,yi):
    '''
    las muestras deben ser pares
    '''
    area = 0
    muestras = len(xi)
    impar = muestras%2
    if impar == 0:
        for i in range(0,muestras-3,3):
            h = (xi[i+3] - xi[i])/3
            deltaA = (3*h/8)*(yi[i]+3*yi[i+1]+3*yi[i+2]+yi[i+3])
            area = area + deltaA
    return(area)

def simpson(xi,yi):
    '''
    Selecciona el tipo de algoritmo Simpson
    '''
    muestras = len(xi)
    impar = muestras%2
    if impar == 1:
        area = simpson13(xi,yi)
    else:
        area = simpson38(xi,yi)
    return(area)
    

# INGRESO
isla = np.array([[0,1,0,0,0],
                 [1,3,1,1,0],
                 [5,4,3,2,0],
                 [0,0,1,1,0]])

xi = np.array([0,100,200,300,400])
yi = np.array([0, 50,100,150])

# PROCEDIMIENTO
tamano = np.shape(isla)
n = tamano[0]
m = tamano[1]

areas = np.zeros(n,dtype = float)
for fila in range(0,n,1):
    unafranja = isla[fila,:]
    areas[fila] = simpson(xi,unafranja)
volumen = simpson(yi,areas)

# SALIDA
print('tramos: ', n,m)
print('areas: ', areas)
print('Volumen: ', volumen)

# Gráfica
X, Y = np.meshgrid(xi, yi)
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.plot_wireframe(X,Y,isla)
plt.show()

s2Eva2017TII_T2 Volumen de isla

Métodos Numéricos

Análisis Numérico