[ compara ] [ resultados ] [ algoritmo ]
..

1. Compara derivadas numéricas con analíticas

Para observar el efecto de disminuir h al aumentar los tramos, se realiza la gráfica de la derivada df/dx analítica versus las derivadas numéricas hacia atrás, hacia centrada y hacia adelante.

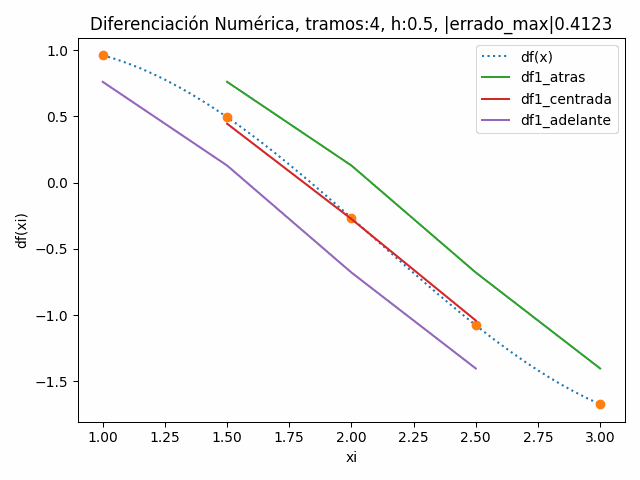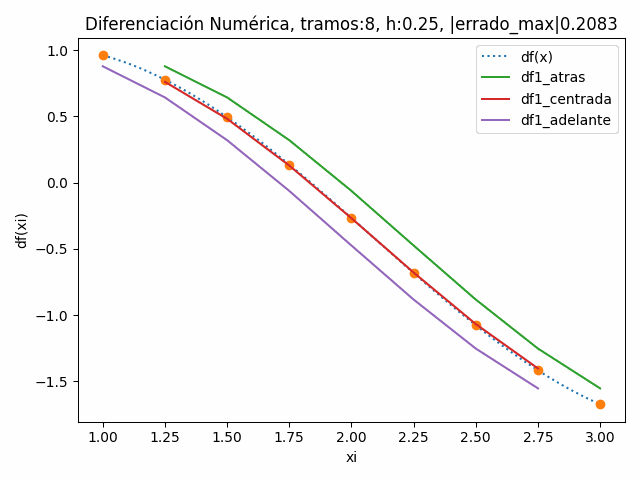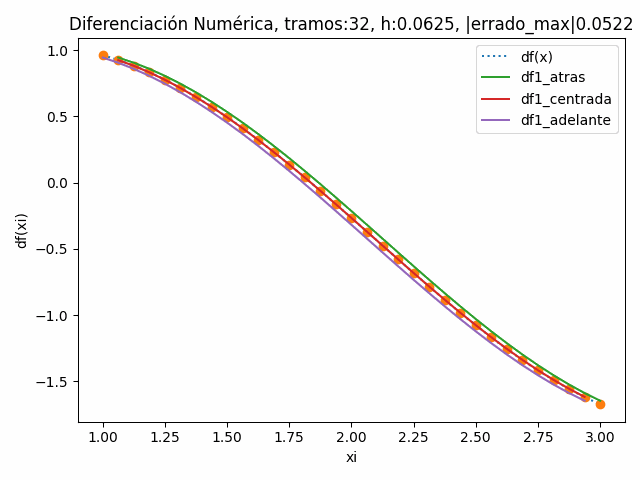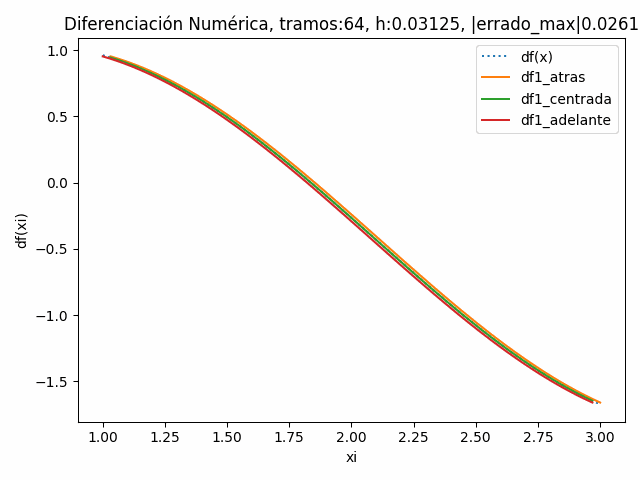
Se observa en la animación la reducción del error en cada diferencia dividida.

[ compara ] [ resultados ] [ algoritmo ]
..

2. Resultados del algoritmo

   tramos: 4 	, h: 0.5
|errado_atras|:    0.3981193548993356
|errado_centro|:   0.04939087954655119
|errado_adelante|: 0.41231110309099034
|errado_max|:      0.41231110309099034
[  dfx,        df1_atras, df1_centro, df1_adelante]
[[ 0.9610378          nan         nan  0.76041177]
 [ 0.49386065  0.76041177  0.44446977  0.12852777]
 [-0.26703531  0.12852777 -0.27540932 -0.67934641]
 [-1.07746577 -0.67934641 -1.04151373 -1.40368104]
 [-1.67397947 -1.40368104         nan         nan]]

   tramos: 8 	, h: 0.25
|errado_atras|:    0.20757887012431775
|errado_centro|:   0.016528173718511008
|errado_adelante|: 0.20828851979214785
|errado_max|:      0.20828851979214785

   tramos: 32 	, h: 0.0625
|errado_atras|:    0.05218398011852454
|errado_centro|:   0.0011877802167017393
|errado_adelante|: 0.052183627077393824
|errado_max|:      0.05218398011852454

   tramos: 64 	, h: 0.03125
|errado_atras|:    0.026094601614190305
|errado_centro|:   0.000302562296112141
|errado_adelante|: 0.026094780174240162
|errado_max|:      094780174240162

[ compara ] [ resultados ] [ algoritmo ]
..

3. Algoritmo con Python

Las instrucciones en Python usadas para la gráfica son:

# Diferenciacion Numerica - 1ra Derivada
# Compara resultados en un intervalo
import numpy as np

# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)
dfx = lambda x: np.sin(x)/(2*np.sqrt(x))+ np.sqrt(x)*np.cos(x)
a = 1  # intervalo de integracion
b = 3
tramos = 64 # >=2, al menos 2 tramos

# PROCEDIMIENTO
muestras = tramos + 1
h = (b-a)/tramos
# puntos de muestras
xi = np.linspace(a,b,muestras)
fi = fx(xi)

# tabla para comparar derivada y diferencias divididas
tabla = np.zeros(shape=(muestras,4),dtype=float)
for i in range(0,muestras,1): # muestras en intervalo
    df1_atras = np.nan ; df1_centro = np.nan; df1_adelante = np.nan
    
    dfxi = dfx(xi[i]) # derivada analitica, como referencia
    if i>0 and i<muestras: # hacia Atras, diferencias divididas
        df1_atras = (fi[i]-fi[i-1])/h
    if i>0 and i<(muestras-1): # Centro, diferencias divididas
        df1_centro = (fi[i+1]-fi[i-1])/(2*h)
    if i>=0 and i<(muestras -1): # hacia Adelante, diferencias divididas
        df1_adelante = (fi[i+1]-fi[i])/h
    tabla[i]=[dfxi,df1_atras,df1_centro,df1_adelante]

# errado desde dfxi
errado_atras = np.max(np.abs(tabla[1:,0]-tabla[1:,1]))
errado_centro = np.max(np.abs(tabla[1:muestras-1,0]-tabla[1:muestras-1,2]))
errado_adelante = np.max(np.abs(tabla[:muestras-1,0]-tabla[:muestras-1,3]))
errado_max = np.max([errado_atras,errado_centro,errado_adelante])

# SALIDA
print('   tramos:', tramos,'\t, h:',h,)
print('|errado_atras|:   ',errado_atras)
print('|errado_centro|:  ',errado_centro)
print('|errado_adelante|:',errado_adelante)
print('|errado_max|:     ',errado_max)
print('[  dfx,        df1_atras, df1_centro, df1_adelante]')
print(tabla)

# GRAFICA
import matplotlib.pyplot as plt

# fx suave aumentando muestras
muestrasfxSuave = tramos*10 + 1
xk = np.linspace(a,b,muestrasfxSuave)
dfk = dfx(xk)

# Graficar f(x), puntos
plt.plot(xk,dfk, label ='df(x)',linestyle='dotted')
if tramos<64:
    plt.plot(xi,tabla[:,0], 'o') # muestras

plt.plot(xi,tabla[:,1],label='df1_atras')
plt.plot(xi,tabla[:,2],label='df1_centrada')
plt.plot(xi,tabla[:,3],label='df1_adelante')

plt.xlabel('xi')
plt.ylabel('df(xi)')
txt = 'Diferenciaci n Num rica'
txt = txt + ', tramos:'+str(tramos)
txt = txt + ', h:'+str(h)
txt = txt + ', |errado_max|'+str(round(errado_max,4))
plt.title(txt)
plt.legend()
plt.tight_layout()

plt.show()

[ compara ] [ resultados ] [ algoritmo ]