Trazador cúbico frontera sujeta [ Algoritmo ] [ gráfica ] [ función ]
..
1. Algoritmo en Python - Frontera sujeta
Para el ejercicio anterior, haciendo que la primera derivada sea cero en los extremos y luego de realizar los ajustes al algoritmo, se tiene como resultado:
h: [0.1 0.1 0.1]
A:
[[-0.03333333 -0.01666667 0. 0. ]
[ 0.1 0.4 0.1 0. ]
[ 0. 0.1 0.4 0.1 ]
[ 0. 0. 0.01666667 0.03333333]]
B: [ -3.5 -27. 24. -3. ]
S: [ 178. -146. 136. -158.]
coeficientes[ ,tramo]:
a: [-540. 470. -490.]
b: [ 89. -73. 68.]
c: [-3.99680289e-15 1.60000000e+00 1.10000000e+00]
d: [1.45 1.8 1.7 ]
Trazador cúbico frontera sujeta
Polinomios por tramos:
x = [ 0.1 , 0.2 ]
expresión: -3.99680288865056e-15*x - 540.0*(x - 0.1)**3 + 89.0000000000001*(x - 0.1)**2 + 1.45
simplifica:
3 2
- 540.0⋅x + 251.0⋅x - 34.0⋅x + 2.88
x = [ 0.2 , 0.3 ]
expresión: 1.6*x + 470.0*(x - 0.2)**3 - 73.0*(x - 0.2)**2 + 1.48
simplifica:
3 2
470.0⋅x - 355.0⋅x + 87.2000000000001⋅x - 5.20000000000001
x = [ 0.3 , 0.4 ]
expresión: 1.1*x - 490.0*(x - 0.3)**3 + 68.0*(x - 0.3)**2 + 1.37
simplifica:
3 2
- 490.0⋅x + 509.0⋅x - 172.0⋅x + 20.72
Instrucciones en Python
# Trazador cubico frontera sujeta import numpy as np import sympy as sym def traza3sujeto(xi,yi,d1y0,dy1n, vertabla=False): ''' trazador cubico sujeto, d1y0=y'(x[0]), dyn=y'(x[n-1]) 1ra derivadas en los nodos extremos son conocidas ''' # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) yi = np.array(yi,dtype=float) n = len(xi) h = np.diff(xi,n=1) # h tamano de paso # Sistema de ecuaciones A = np.zeros(shape=(n,n), dtype=float) B = np.zeros(n, dtype=float) S = np.zeros(n-1, dtype=float) A[0,0] = -h[0]/3 A[0,1] = -h[0]/6 B[0] = d1y0 - (yi[1]-yi[0])/h[0] for i in range(1,n-1,1): A[i,i-1] = h[i-1] A[i,i] = 2*(h[i-1]+h[i]) A[i,i+1] = h[i] B[i] = 6*((yi[i+1]-yi[i])/h[i] - (yi[i]-yi[i-1])/h[i-1]) A[n-1,n-2] = h[n-2]/6 A[n-1,n-1] = h[n-2]/3 B[n-1] = d1yn - (yi[n-1]-yi[n-2])/h[n-2] # Resolver sistema de ecuaciones, S S = np.linalg.solve(A,B) # Coeficientes a = np.zeros(n-1, dtype = float) b = np.zeros(n-1, dtype = float) c = np.zeros(n-1, dtype = float) d = np.zeros(n-1, dtype = float) for j in range(0,n-1,1): a[j] = (S[j+1]-S[j])/(6*h[j]) b[j] = S[j]/2 c[j] = (yi[j+1]-yi[j])/h[j] - (2*h[j]*S[j]+h[j]*S[j+1])/6 d[j] = yi[j] # Polinomio trazador x = sym.Symbol('x') px_tabla = [] for j in range(0,n-1,1): pxtramo = a[j]*(x-xi[j])**3 + b[j]*(x-xi[j])**2 + c[j]*(x-xi[j])+ d[j] px_tabla.append(pxtramo) if vertabla==True: print('h:',h) print('A:') ; print(A) print('B:',B) ; print('S:',S) print('coeficientes[ ,tramo]:') print('a:',a) ; print('b:',b) print('c:',c) ; print('d:',d) return(px_tabla) # PROGRAMA --------------- # INGRESO xi = [0.1 , 0.2, 0.3, 0.4] fi = [1.45, 1.8, 1.7, 2.0] titulo = 'Trazador cúbico frontera sujeta' # sujeto, 1ra derivadas en los nodos extremos son conocidas d1y0 = 0 # izquierda, xi[0] d1yn = 0 # derecha, xi[n-1] # PROCEDIMIENTO n = len(xi) # Obtiene los polinomios por tramos px_tabla = traza3sujeto(xi,fi,d1y0,d1yn,vertabla=True) # SALIDA print(titulo) print('Polinomios por tramos: ') for i in range(0,n-1,1): print('x = [',xi[i],',',xi[i+1],']') print('expresión:',px_tabla[i]) print('simplifica:') sym.pprint(px_tabla[i].expand())
Trazador cúbico frontera sujeta [ Algoritmo ] [ gráfica ] [ función ]
..
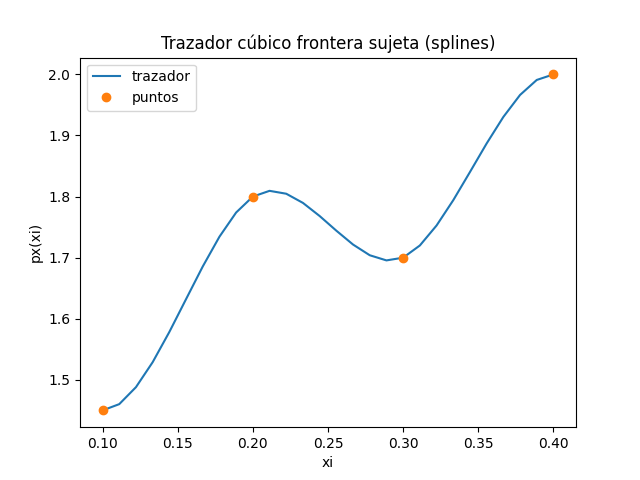
2. Gráfica en Python
La gráfica se realiza en un bloque con los resultados del algoritmo
# GRAFICA -------------- import matplotlib.pyplot as plt muestras = 10 # entre cada par de puntos # Puntos para grafica en cada tramo xtraza = np.array([],dtype=float) ytraza = np.array([],dtype=float) i = 0 while i<n-1: # cada tramo xtramo = np.linspace(xi[i],xi[i+1],muestras) # evalua polinomio del tramo pxk = sym.lambdify('x',px_tabla[i]) ytramo = pxk(xtramo) # vectores de trazador en x,y xtraza = np.concatenate((xtraza,xtramo)) ytraza = np.concatenate((ytraza,ytramo)) i = i + 1 # Graficar plt.plot(xtraza,ytraza, label='trazador') plt.plot(xi,fi,'o', label='puntos') plt.title(titulo) plt.xlabel('xi') plt.ylabel('px(xi)') plt.legend() plt.show() plt.show()
Trazador cúbico frontera sujeta [ Algoritmo ] [ gráfica ] [ función ]
..
3. Trazador cúbico sujeto como función en Scipy.interpolate.CubicSpline
También es posible usar la función de Scipy para generar los trazadores cúbicos en el caso de frontera sujeta. Se hacen los ajustes en el bloque de ingreso, considerando que las primeras derivadas en los nodos extremos son conocidas.
# Trazador cúbico frontera sujeta con Scipy import numpy as np import scipy as sp import sympy as sym # INGRESO xi = [0.1 , 0.2, 0.3, 0.4] fi = [1.45, 1.8, 1.7, 2.0] titulo = 'Trazador cúbico frontera sujeta' # sujeto, 1ra derivadas en los nodos extremos son conocidas d1y0 = 0 # izquierda, xi[0] d1yn = 0 # derecha, xi[n-1] cs_tipo = ((1, d1y0), (1, d1yn)) # sujeto # PROCEDIMIENTO # Vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) # coeficientes de trazadores cúbicos traza_c = sp.interpolate.CubicSpline(xi,fi,bc_type=cs_tipo ) traza_coef = traza_c.c # coeficientes a = traza_coef[0] b = traza_coef[1] c = traza_coef[2] d = traza_coef[3] # Polinomio trazador x = sym.Symbol('x') px_tabla = [] for j in range(0,n-1,1): pxtramo = a[j]*(x-xi[j])**3 + b[j]*(x-xi[j])**2 + c[j]*(x-xi[j])+ d[j] px_tabla.append(pxtramo) # SALIDA print(titulo) print('coeficientes:') print('a:',a) print('b:',b) print('c:',c) print('d:',d) print('Polinomios por tramos: ') for i in range(0,n-1,1): print('x = [',xi[i],',',xi[i+1],']') print('expresión:',px_tabla[i]) print('simplifica:') sym.pprint(px_tabla[i].expand())
La gráfica se puede realizar con el bloque presentado para el algoritmo anterior. El resultado del algoritmo se presenta como
Trazador cúbico frontera sujeta
coeficientes:
a: [-540. 470. -490.]
b: [ 89. -73. 68.]
c: [0. 1.6 1.1]
d: [1.45 1.8 1.7 ]
Polinomios por tramos:
x = [ 0.1 , 0.2 ]
expresión: -540.0*(x - 0.1)**3 + 89.0*(x - 0.1)**2 + 1.45
simplifica:
3 2
- 540.0⋅x + 251.0⋅x - 34.0⋅x + 2.88
x = [ 0.2 , 0.3 ]
expresión: 1.6*x + 470.0*(x - 0.2)**3 - 73.0*(x - 0.2)**2 + 1.48
simplifica:
3 2
470.0⋅x - 355.0⋅x + 87.2000000000001⋅x - 5.2
x = [ 0.3 , 0.4 ]
expresión: 1.1*x - 490.0*(x - 0.3)**3 + 68.0*(x - 0.3)**2 + 1.37
simplifica:
3 2
- 490.0⋅x + 509.0⋅x - 172.0⋅x + 20.72
Trazador cúbico frontera sujeta [ Algoritmo ] [ gráfica ] [ función ]