Ejercicio: 1Eva2007TIII_T3 Factorar polinomio

Para factorizar el polinomio:

Se realiza la gráfica para observar los intervalos de búsqueda de raíces.

Para la solución con Newton-Raphson se plantea f(x)=0

Para la primera raíz a la izquierda, se usa x0 = 0

itera = 0

itera = 1

itera = 2

como el error es del orden de 10^-6 que es menor que tolera de 10^-5 se considera la raíz encontrada.

raíz en: 0.03539136103889022

los resultados con el algoritmo son:

i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 0.     -0.1     3.      0.0333  0.0333]
1 [ 3.3333e-02 -5.4815e-03  2.6733e+00  3.5384e-02  2.0504e-03]
2 [ 3.5384e-02 -2.0163e-05  2.6537e+00  3.5391e-02  7.5982e-06]
raíz en:  0.03539136103889022

para raíz cerca de 1

i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 1.  -0.1 -1.   0.9  0.1]
1 [ 0.9    0.008 -1.14   0.907  0.007]
2 [ 9.0702e-01  2.0390e-05 -1.1341e+00  9.0704e-01  1.7979e-05]
raíz en:  0.9070355226186211

para raíz cercana a 1.5

i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 1.5    -0.1     1.5     1.5667  0.0667]
1 [1.5667 0.0184 2.06   1.5577 0.0089]
2 [1.5577e+00 3.4849e-04 1.9820e+00 1.5576e+00 1.7583e-04]
3 [1.5576e+00 1.3436e-07 1.9805e+00 1.5576e+00 6.7843e-08]
raíz en:  1.557573116112315

Algoritmo en Python

# 1ra Eval III Término 2007
# Tema 3. Factorar polinomio
import numpy as np
import matplotlib.pyplot as plt

def newton_raphson(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4):
    '''
    fx y dfx en forma numérica lambda
    xi es el punto inicial de búsqueda
    '''
    itera=0
    tramo = abs(2*tolera)
    if vertabla==True:
        print('método de Newton-Raphson')
        print('i', ['xi','fi','dfi', 'xnuevo', 'tramo'])
        np.set_printoptions(precision)
    while (tramo>=tolera):
        fi = fx(xi)
        dfi = dfx(xi)
        xnuevo = xi - fi/dfi
        tramo = abs(xnuevo-xi)
        if vertabla==True:
            print(itera,np.array([xi,fi,dfi,xnuevo,tramo]))
        xi = xnuevo
        itera = itera + 1

    if itera>=iteramax:
        xi = np.nan
        print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones')

    return(xi)

# Literal a)
fx = lambda x: 2*x**3 - 5*x**2 + 3*x -0.1
dfx = lambda x: 6*x**2 - 10*x +3
# Literal b)
#fx =  lambda x: (2*x**3 - 5*x**2 + 3*x -0.1)/(x-0.03539136103889022)
#dfx = lambda x: (6*x**2 - 10*x + 3)/(x - 0.0353913610388902) - (2*x**3 - 5*x**2 + 3*x - 0.1)/(x - 0.0353913610388902)**2

x0 = 0
tolera = 0.0001

# PROCEDIMIENTO
respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True)

# SALIDA
print('raíz en: ', respuesta)

# simplificando el polinomio
import sympy as sym
x = sym.Symbol('x')
p = 2*x**3 - 5*x**2 + 3*x -0.1
Q2 = p/(x-respuesta)
dQ2 = sym.diff(Q2,x,1)
print('Q2')
print(Q2)
print('dQ2')
print(dQ2)


# grafica
a = 0
b = 2
muestras = 21
xi = np.linspace(a,b, muestras)
fi = fx(xi)
plt.plot(xi,fi, label='P(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('P3(x)')
plt.axhline(0)
plt.grid()
plt.show()

literal b

Obtenga el polinomio cociente Q₂(x), a partir de P₃(x) = (x – r₁)Q₂(x)

Se simplifica el polinomio realizando la división:

Se reutiliza el algoritmo usando las nuevas expresiones

# Literal b)
# PROCEDIMIENTO
fx =  lambda x: (2*x**3 - 5*x**2 + 3*x -0.1)/(x-raiz1)
dfx = lambda x: (6*x**2 - 10*x + 3)/(x - 0.0353913610388902) - (2*x**3 - 5*x**2 + 3*x - 0.1)/(x - 0.0353913610388902)**2

la derivada se puede obtener usando la librería Sympy, con las instrucciones:

# simplificando el polinomio
import sympy as sym
x = sym.Symbol('x')
p = 2*x**3 - 5*x**2 + 3*x -0.1
Q2 = p/(x-respuesta)
dQ2 = sym.diff(Q2,x,1)
print('Q2')
print(Q2)
print('dQ2')
print(dQ2)

Usando los resultados de Q2(x) y actualizando las expresiones para f(x) y f'(x) se obtienen los siguientes resultados, que verifican las raíces encontradas en el literal a.

i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 0.      2.8255 -4.9292  0.5732  0.5732]
1 [ 0.5732  0.6572 -2.6363  0.8225  0.2493]
2 [ 0.8225  0.1243 -1.6392  0.8983  0.0758]
3 [ 0.8983  0.0115 -1.336   0.9069  0.0086]
4 [ 9.0692e-01  1.4809e-04 -1.3015e+00  9.0704e-01  1.1379e-04]
5 [ 9.0704e-01  2.5894e-08 -1.3011e+00  9.0704e-01  1.9902e-08]
raíz en:  0.9070355227446406

La gráfica obtenida para Q2(x) es:

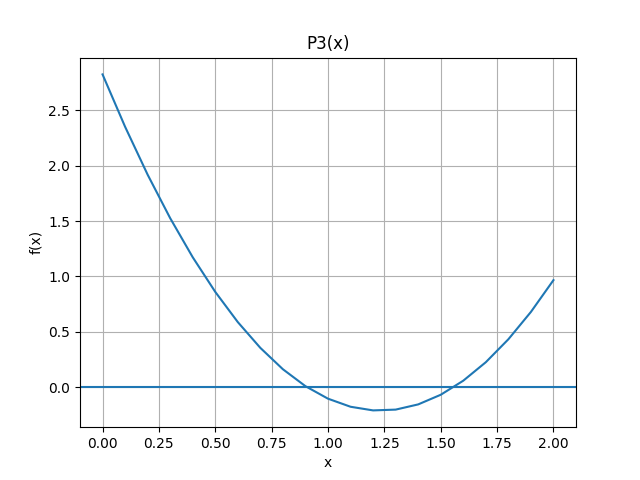
literal c

La otra raíz cercana a 1.5 se calcula a partir de Q2(x) usando el algoritmo.

i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 1.5    -0.0683  1.0708  1.5638  0.0638]
1 [1.5638 0.0081 1.3258 1.5576 0.0061]
2 [1.5576e+00 7.5234e-05 1.3013e+00 1.5576e+00 5.7814e-05]
raíz en:  1.5575731212503858

literal d

El polinomio:

se expresa también formado como parte de sus raíces: