Ejercicio: 3Eva2020PAOI_T3 EDP Parabólica centro triángulo
\frac{\partial u}{\partial t} - c^2 \frac{\partial ^2 u}{\partial x^2} = g(x)Literal a. gráfica de malla

literal b. Planteamiento
Reordena ecuación para derivada de mayor orden
\frac{\partial u}{\partial t} - c^2 \frac{\partial ^2 u}{\partial x^2} = g(x) \frac{\partial u}{\partial t}- g(x) = c^2 \frac{\partial ^2 u}{\partial x^2} \frac{\partial ^2 u}{\partial x^2} = \frac{1}{c^2} \left( \frac{\partial u}{\partial t}- g(x) \right) \frac{\partial ^2 u}{\partial x^2} = \frac{1}{c^2} \frac{\partial u}{\partial t} - \frac{g(x)}{c^2}literal c. Modelo discreto
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = \frac{1}{c^2} \frac{u_{i,j+1}-u_{i,j}}{\Delta t} - \frac{g(x)}{c^2}agrupando constantes
\Delta t \left( \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} \right)=\left( \frac{1}{c^2} \frac{u_{i,j+1}-u_{i,j}}{\Delta t} - \frac{g(x)}{c^2} \right) c^2 \Delta t \frac{c^2 \Delta t}{(\Delta x)^2} \left( u_{i+1,j}-2u_{i,j}+u_{i-1,j} \right)= u_{i,j+1}-u_{i,j} - g(x)\Delta t \lambda = \frac{c^2 \Delta t}{(\Delta x)^2}Analiza λ para convergencia del método
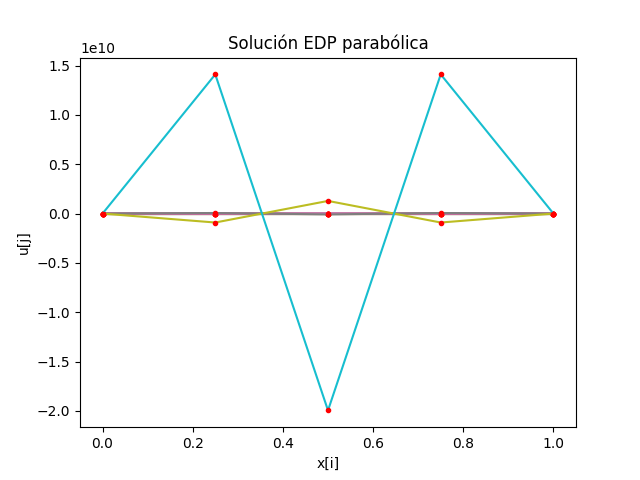
\lambda = \frac{c^2 \Delta t}{(\Delta x)^2} = \frac{1^2(0.05)}{0.25^2} = 0.8como λ>0.5 el método NO converge.
se debe ajustar uno de los tamaños de paso, por ejemplo Δt = 0.25 o la mitad del valor anterior para que el método sea convergente. Se puede probar también con el algoritmo y la gráfica resultante.
cambiando dt = 0.025, λ>0.4, el resultado es la barra enfriando el centro cuando pasa el tiempo.
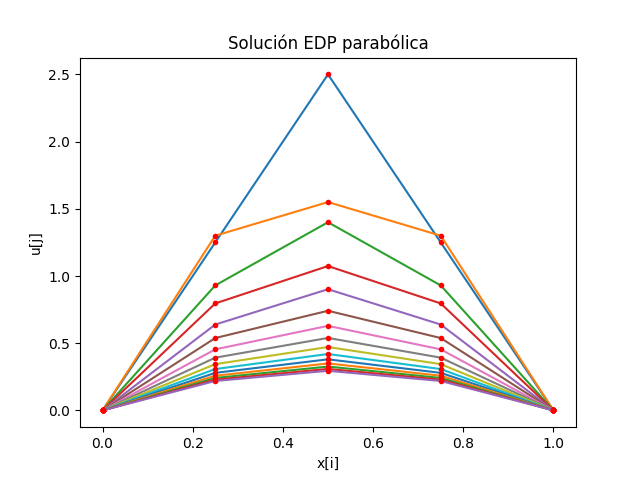
literal d. Usando el método explícito
reagrupando nodos
\lambda \left( u_{i+1,j}-2u_{i,j}+u_{i-1,j} \right)= u_{i,j+1}-u_{i,j} - g(x)\Delta t \lambda u_{i+1,j}-2\lambda u_{i,j} + \lambda u_{i-1,j} = u_{i,j+1}-u_{i,j} - g(x)\Delta t \lambda u_{i+1,j}-2\lambda u_{i,j} + \lambda u_{i-1,j} +u_{i,j} + g(x)\Delta t = u_{i,j+1} \lambda u_{i+1,j} + (1 -2\lambda) u_{i,j} + \lambda u_{i-1,j} + g(x)\Delta t = u_{i,j+1}que es la fórmula a usar en el algoritmo
Algoritmo en Python
El resultado del algoritmo se muestra como:
Método explícito EDP Parabólica
lambda: 0.4
x: [0. 0.25 0.5 0.75 1. ]
t: [0. 0.03 0.05 0.08 0.1 ] ... 0.375
Tabla de resultados en malla EDP Parabólica
j, U[:,: 5 ], primeras iteraciones de 15
5 [0. 0.54 0.74 0.54 0. ]
4 [0. 0.64 0.9 0.64 0. ]
3 [0. 0.8 1.07 0.8 0. ]
2 [0. 0.93 1.4 0.93 0. ]
1 [0. 1.3 1.55 1.3 0. ]
0 [0. 1.25 2.5 1.25 0. ]

#3ra Evaluación 2020-2021 PAO I. 22/Septiembre/2020
# EDP parabólicas d2u/dx2 = K du/dt
# método explícito,usando diferencias divididas
import numpy as np
# INGRESO
# Valores de frontera
Ta = 0 # izquierda de barra
Tb = 0 # derecha de barra
#Tc = 25 # estado inicial de barra en x
# f(x) en tiempo inicial
f1 = lambda x: 5*x
f2 = lambda x: 5*(1-x)
fxc = lambda x: np.piecewise(x,
[x<0.5, x>=0.5],
[f1,f2])
# dimensiones de la barra
a = 0 # longitud en x
b = 1
t0 = 0 # tiempo inicial, aumenta con dt en n iteraciones
C = 1
K = 1/(C**2) # Constante K
dx = 0.25 # muestreo en x, tamaño de paso
dt = 0.05 # sin ajuste de convergencia
dt = dt/2 # con ajuste para convergencia
gx = 2
n = 15 # iteraciones en tiempo
verdigitos = 2 # decimales a mostrar en tabla de resultados
# coeficientes de U[x,t]. factores P,Q,R,
lamb = dt/(K*dx**2)
P = lamb # izquierda P*U[i-1,j]
Q = 1 - 2*lamb # centro Q*U[i,j]
R = lamb # derecha R*U[i+1,j]
# PROCEDIMIENTO
# iteraciones en x, longitud
xi = np.arange(a,b+dx/2,dx)
m = len(xi)
ultimox = m-1
ultimot = n-1
# u[xi,tj], tabla de resultados
# se incluye el estado a t=0: n+1
u = np.zeros(shape=(m,n+1), dtype=float)
# u[i,j], valores iniciales
u[0,:] = Ta # Izquierda
u[ultimox,:] = Tb # derecha
# estado inicial de barra en x, Tc
fic = fxc(xi) # f(x) en tiempo inicial
u[1:ultimox,0] = fic[1:ultimox]
# Calcula U para cada tiempo + dt
tj = np.arange(t0,(n+1)*dt,dt)
for j in range(0,n,1):
for i in range(1,ultimox,1):
# ecuacion discreta, entre [1,ultimox]
u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j] + gx*dt
# SALIDA
j_mostrar = 5
np.set_printoptions(precision=verdigitos)
print('Método explícito EDP Parabólica')
print('lambda: ',np.around(lamb,verdigitos))
print('x:',xi)
print('t:',tj[0:j_mostrar],'...',tj[-1])
print('Tabla de resultados en malla EDP Parabólica')
print('j, U[:,:',j_mostrar,'], primeras iteraciones de ',n)
for j in range(j_mostrar,-1,-1):
print(j,u[:,j])
Gráfica con Python
# GRAFICA ------------
import matplotlib.pyplot as plt
tramos = 10
salto = int(n/tramos) # evita muchas líneas
if (salto == 0):
salto = 1
for j in range(0,n,salto):
vector = u[:,j]
plt.plot(xi,vector)
plt.plot(xi,vector, '.',color='red')
plt.xlabel('x[i]')
plt.ylabel('u[j]')
plt.title('Solución EDP parabólica')
plt.show()
# GRAFICA en 3D ------
tj = np.arange(0,n*dt,dt)
tk = np.zeros(tramos,dtype=float)
# Extrae parte de la matriz U,acorde a los tramos
U = np.zeros(shape=(m,tramos),dtype=float)
for k in range(0,tramos,1):
U[:,k] = u[:,k*salto]
tk[k] = tj[k*salto]
# Malla para cada eje X,Y
Xi, Yi = np.meshgrid(xi,tk)
U = np.transpose(U)
fig_3D = plt.figure()
graf_3D = fig_3D.add_subplot(111, projection='3d')
graf_3D.plot_wireframe(Xi,Yi,U, color ='blue')
graf_3D.plot(xi[0],tk[1],U[1,0],'o',color ='orange')
graf_3D.plot(xi[1],tk[1],U[1,1],'o',color ='green')
graf_3D.plot(xi[2],tk[1],U[1,2],'o',color ='green')
graf_3D.plot(xi[1],tk[2],U[2,1],'o',color ='salmon',
label='U[i,j+1]')
graf_3D.set_title('EDP Parabólica')
graf_3D.set_xlabel('x')
graf_3D.set_ylabel('t')
graf_3D.set_zlabel('U')
graf_3D.legend()
graf_3D.view_init(35, -45)
plt.show()