Ejercicio: 1Eva2008TII_T3_MN Ganancia en inversión
Se dispone de los datos (x, f(x)), en donde x es un valor de inversión y f(x) es un valor de ganancia, ambos en miles de dólares.
xi = [3.2 , 3.8 , 4.2 , 4.5 ]
fi = [5.12, 6.42, 7.25, 6.85]Los datos se usan junto al modelo propuesto:
f(x) = a_1 x^3 + a_2 x^2 + a_3 x + a_4generando las expresiones del sistema de ecuaciones:
a_1 (3.2)^3 + a_2 (3.2)^2 + a_3 (3.2) + a_4 = 5.12 a_1 (3.8)^3 + a_2 (3.8)^2 + a_3 (3.8) + a_4 = 6.42 a_1 (4.2)^3 + a_2 (4.2)^2 + a_3 (4.2) + a_4 = 7.25 a_1 (4.5)^3 + a_2 (4.5)^2 + a_3 (4.5) + a_4 = 6.85Se convierte a la forma Ax=B
\begin{bmatrix} (3.2)^3 && (3.2)^2 && (3.2) && 1 \\ (3.8)^3 && (3.8)^2 && (3.8) && 1 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 \\ (4.5)^3 && (4.5)^2 && (4.5) && 1 \end{bmatrix} . \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{bmatrix} = \begin{bmatrix} 5.12 \\ 6.42 \\ 7.25 \\6.85 \end{bmatrix}Se crea la matriz aumentada
\begin{bmatrix} (3.2)^3 && (3.2)^2 && (3.2) && 1 && 5.12\\ (3.8)^3 && (3.8)^2 && (3.8) && 1 && 6.42 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 && 7.25 \\ (4.5)^3 && (4.5)^2 && (4.5) && 1 && 6.85 \end{bmatrix}Se pivotea por filas:
\begin{bmatrix} (4.5)^3 && (4.5)^2 && (4.5) && 1 && 6.85 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 && 7.25 \\ (3.8)^3 && (3.8)^2 && (3.8) && 1 && 6.42 \\ (3.2)^3 && (3.2)^2 && (3.2) && 1 && 5.12 \end{bmatrix}Como se pide un método directo, se inicia con el algoritmo de eliminación hacia adelante con factor para cada fila a partir de la diagonal.
\begin{bmatrix} (4.5)^3 && (4.5)^2 && (4.5) \\ (4.2)^3 - (4.5)^3\frac{(4.2)^3}{(4.5)^3} && (4.2)^2 - (4.5)^2\frac{(4.2)^3}{(4.5)^3} && (4.2) - (4.5)\frac{(4.2)^3}{(4.5)^3} \\ (3.8)^3 - (4.5)^3\frac{(3.8)^3}{(4.5)^3} && (3.8)^2 - (4.5)^2\frac{(3.8)^3}{(4.5)^3} && (3.8) -(4.5)\frac{(3.8)^3}{(4.5)^3} \\ (3.2)^3 - (4.5)^3\frac{(3.2)^3}{(4.5)^3} && (3.2)^2 -(4.5)^2\frac{(3.2)^3}{(4.5)^3} && (3.2) - (4.5)\frac{(3.2)^3}{(4.5)^3} \end{bmatrix}continua a la derecha de la matriz:
\begin{bmatrix} 1 && 6.85 \\ 1 - 1\frac{(4.2)^3}{(4.5)^3} && 7.25 - 6.85\frac{(4.2)^3}{(4.5)^3} \\ 1 -1\frac{(3.8)^3}{(4.5)^3} && 6.42 - 6.85\frac{(3.8)^3}{(4.5)^3}\\1 -1\frac{(3.2)^3}{(4.5)^3} && 5.12-6.85\frac{(3.2)^3}{(4.5)^3} \end{bmatrix}Pivoteo parcial por filas AB: ----
[[91.125 20.25 4.5 1. 6.85 ]
[74.088 17.64 4.2 1. 7.25 ]
[54.872 14.44 3.8 1. 6.42 ]
[32.768 10.24 3.2 1. 5.12 ]]
Eliminación hacia adelante: ------
i: 0 k: 1 factor: 0.8130370370370371
i: 0 k: 2 factor: 0.6021618655692729
i: 0 k: 3 factor: 0.35959396433470514
[[91.125 20.25 4.5 1. 6.85 ]
[ 0. 1.176 0.5413 0.187 1.6807]
[ 0. 2.2462 1.0903 0.3978 2.2952]
[ 0. 2.9582 1.5818 0.6404 2.6568]]
i: 1 k: 2 factor: 1.9100529100529142
i: 1 k: 3 factor: 2.5154950869236625
[[ 9.1125e+01 2.0250e+01 4.5000e+00 1.0000e+00 6.8500e+00]
[ 0.0000e+00 1.1760e+00 5.4133e-01 1.8696e-01 1.6807e+00]
[ 0.0000e+00 0.0000e+00 5.6296e-02 4.0729e-02 -9.1503e-01]
[ 0.0000e+00 0.0000e+00 2.2011e-01 1.7010e-01 -1.5710e+00]]
i: 2 k: 3 factor: 3.9097744360903106
[[ 9.1125e+01 2.0250e+01 4.5000e+00 1.0000e+00 6.8500e+00]
[ 0.0000e+00 1.1760e+00 5.4133e-01 1.8696e-01 1.6807e+00]
[ 0.0000e+00 0.0000e+00 5.6296e-02 4.0729e-02 -9.1503e-01]
[ 0.0000e+00 0.0000e+00 0.0000e+00 1.0860e-02 2.0065e+00]]
Eliminación hacia atras: ------
i: 3 pivote: 0.010860484544693044
k: 2 factor: 3.7501994302000807
k: 1 factor: 17.214974358977564
k: 0 factor: 92.07692307694026
[[ 9.1125e+01 2.0250e+01 4.5000e+00 0.0000e+00 -1.7791e+02]
[ 0.0000e+00 1.1760e+00 5.4133e-01 0.0000e+00 -3.2862e+01]
[ 0.0000e+00 0.0000e+00 5.6296e-02 0.0000e+00 -8.4400e+00]
[ 0.0000e+00 0.0000e+00 0.0000e+00 1.0860e-02 2.0065e+00]]
i: 2 pivote: 0.05629629629629451
k: 1 factor: 9.615789473684513
k: 0 factor: 79.93421052631832
[[ 9.1125e+01 2.0250e+01 0.0000e+00 0.0000e+00 4.9674e+02]
[ 0.0000e+00 1.1760e+00 0.0000e+00 0.0000e+00 4.8295e+01]
[ 0.0000e+00 0.0000e+00 5.6296e-02 0.0000e+00 -8.4400e+00]
[ 0.0000e+00 0.0000e+00 0.0000e+00 1.0000e+00 1.8476e+02]]
i: 1 pivote: 1.1759999999999984
k: 0 factor: 17.219387755102066
[[ 91.125 0. 0. 0. -334.876 ]
[ 0. 1.176 0. 0. 48.2952]
[ 0. 0. 1. 0. -149.9209]
[ 0. 0. 0. 1. 184.7569]]
i: 0 pivote: 91.125
[[ 91.125 0. 0. 0. -334.876 ]
[ 0. 1. 0. 0. 41.0673]
[ 0. 0. 1. 0. -149.9209]
[ 0. 0. 0. 1. 184.7569]]
AB:
[[ 1. 0. 0. 0. -3.6749]
[ 0. 1. 0. 0. 41.0673]
[ 0. 0. 1. 0. -149.9209]
[ 0. 0. 0. 1. 184.7569]]
Método de Gauss-Jordan
solución X:
[ -3.6749 41.0673 -149.9209 184.7569]con lo que el polinomio buscado es:
f(x) = -3.67490842 x^3 + 41.06730769 x^2 + -149.92086081 x + 184.75692308que genera la siguiente gráfica:
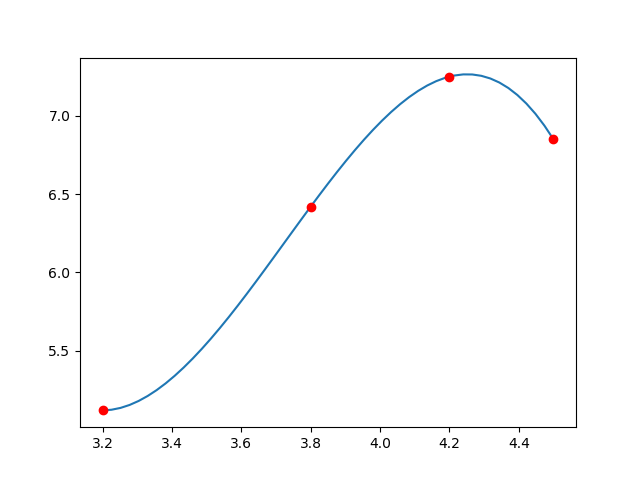
para encontrar la cantidad necesaria a invertir y obtener 6.0 de ganancia en f(x):
6.0 = -3.67490842 x^3 + 41.06730769 x^2 + -149.92086081 x + 184.75692308que para usar en el algoritmo se realiza se reordena como g(x) = 0
-3.67490842 x^3 + 41.06730769 x^2 + -149.92086081 x + 184.75692308 - 6.0 = 0y se aplica la búsqueda de raíces en el rango [a, b] que de la gráfica se estima en [3.2, 3.8]
La ejecución del algoritmo de búsqueda queda como tarea.
Algoritmo en Python
para obtener la gráfica y respuesta a la matriz:
# Método de Gauss-Jordan
# Sistemas de Ecuaciones A.X=B
import numpy as np
# INGRESO
xi = [3.2 , 3.8 , 4.2 , 4.5 ]
fi = [5.12, 6.42, 7.25, 6.85]
A = [[4.5**3 , 4.5**2 , 4.5 , 1],
[4.2**3 , 4.2**2 , 4.2 , 1],
[3.8**3 , 3.8**2 , 3.8 , 1],
[3.2**3 , 3.2**2 , 3.2 , 1]]
B = [6.85,7.25,6.42,5.12]
# PROCEDIMIENTO
np.set_printoptions(precision=4)
casicero = 1e-15
# Matrices como arreglo, numeros reales
A = np.array(A,dtype=float)
B = np.array(B,dtype=float)
# Matriz aumentada AB
B_columna = np.transpose([B])
AB = np.concatenate((A,B_columna),axis=1)
# Pivoteo parcial por filas
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
# Para cada fila en AB
for i in range(0,n-1,1):
# columna desde diagonal i en adelante
columna = abs(AB[i:,i])
dondemax = np.argmax(columna)
if (dondemax !=0): # NO en diagonal
# intercambia filas
temporal = np.copy(AB[i,:])
AB[i,:] = AB[dondemax+i,:]
AB[dondemax+i,:] = temporal
print('Pivoteo parcial por filas AB: ----')
print(AB)
# Eliminación hacia adelante
print('Eliminación hacia adelante: ------')
for i in range(0,n-1,1): # una fila
pivote = AB[i,i]
adelante = i + 1
for k in range(adelante,n,1): # diagonal adelante
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - AB[i,:]*factor
print('i:',i,'k:',k, 'factor:',factor)
print(AB)
# Eliminación hacia atras
print('Eliminación hacia atras: ------')
ultfila = n-1
ultcolumna = m-1
for i in range(ultfila,0-1,-1): # una fila
pivote = AB[i,i]
print('i:',i,' pivote:',pivote)
atras = i - 1
for k in range(atras,0-1,-1): # diagonal adelante
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - AB[i,:]*factor
for j in range(0,m,1): # casicero revisa
if abs(AB[k,j])<casicero:
AB[k,j]=0
print(' k:',k, 'factor:',factor)
print(AB)
AB[i,:] = AB[i,:]/AB[i,i] # diagonal a unos
print('AB:')
print(AB)
X = np.copy(AB[:,ultcolumna])
# SALIDA
print('Método de Gauss-Jordan')
print('solución X: ')
print(X)
# Revisa polinomio
import matplotlib.pyplot as plt
a = np.min(xi)
b = np.max(xi)
muestras = 21
px = lambda x: X[0]*x**3 + X[1]*x**2 +X[2]*x + X[3]
xk = np.linspace(a,b,muestras)
pxk = px(xk)
# gráfica
plt.plot(xk,pxk)
plt.plot(xi,fi,'ro')
plt.show()