Ejercicio: 3Eva2017TI_T3 Sustancia en lago
El ejercicio se divide en dos partes: sección transversal con la derivada y concentración promedio con integrales.
Sección transversal
Se calcula la derivada con una aproximación básica con error O(h)
f'(x_i) = \frac{f(x_{i+1})-f(x_i)}{h} + O(h)repitiendo la fórmula entre cada par de puntos consecutivos
dv/dz: [-1.1775 -0.7875 -0.39175 -0.09825 0. ]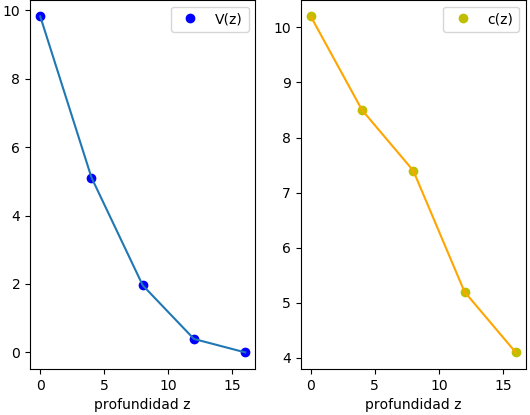
Concentración promedio
Para los integrales usamos la regla del trapecio:
I = (b-a) \frac{f(a)+f(b)}{2}numerador: 224.38960000000003
denominador: 29.852
concentracion promedio: 7.516735897092323Aplicando los algoritmos en Python para todos los puntos:
# 3Eva_IT2017_T3 Sustancia en lago
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
zi = np.array([0. , 4 , 8 , 12 , 16])
vi = np.array([9.82, 5.11, 1.96, 0.393, 0.])
ci = np.array([10.2, 8.5 , 7.4 , 5.2 , 4.1])
# PROCEDIMIENTO
n = len(zi)
# primera derivada hacia adelante con error O(h)
dv = np.zeros(n,dtype=float)
for i in range(0,n-1,1):
h = zi[i+1]-zi[i]
dv[i]=(vi[i+1]-vi[i])/h
As = -dv*zi
# integrales por rectángulo
numerador = 0
for i in range(0,n-1,1):
altura = (ci[i]*As[i]+ci[i+1]*As[i+1])/2
numerador = numerador +altura*(zi[i+1]-zi[i])
denominador = 0
for i in range(0,n-1,1):
altura = (As[i]+As[i+1])/2
denominador = denominador +altura*(zi[i+1]-zi[i])
cpromedio = numerador/denominador
# SALIDA
print('dv/dz: ')
print(dv)
print('numerador: ',numerador)
print('denominador: ',denominador)
print('concentracion promedio: ',cpromedio)
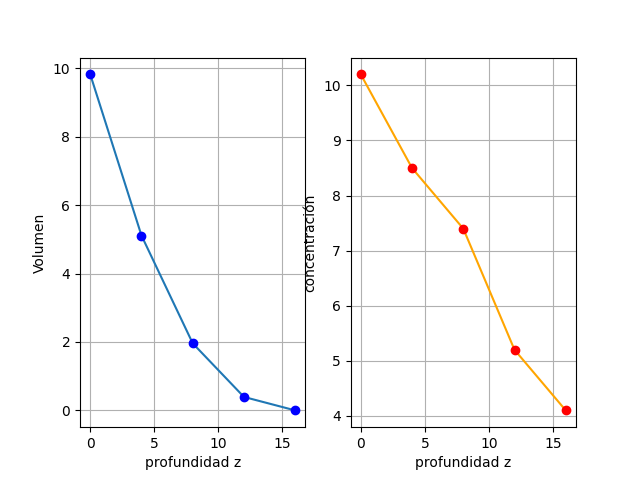
# Grafica
plt.subplot(121)
plt.plot(zi,vi)
plt.plot(zi,vi,'bo')
plt.xlabel('profundidad z')
plt.ylabel('Volumen')
plt.grid()
plt.subplot(122)
plt.plot(zi,ci, color = 'orange')
plt.plot(zi,ci,'ro')
plt.xlabel('profundidad z')
plt.ylabel('concentración')
plt.grid()
plt.show()