5.2 Regla de Simpson 1/3 para Integración numérica con Python

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]

..

1. La regla de Simpson 1/3

Referencia: Chapra 21.2.1 p631, Burden 4.3 p144, Rodríguez 7.1.4 p281

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)]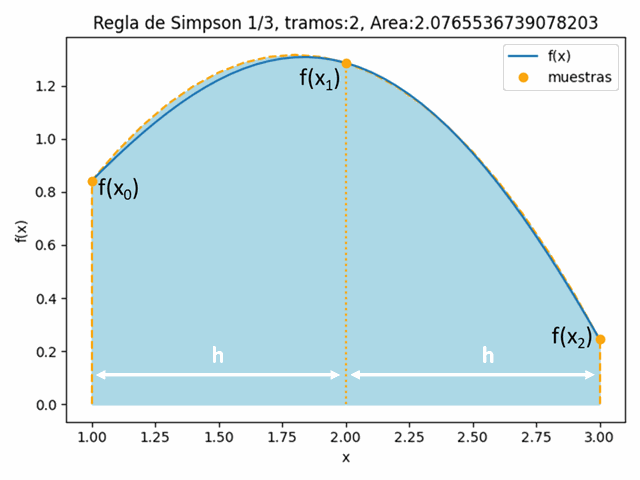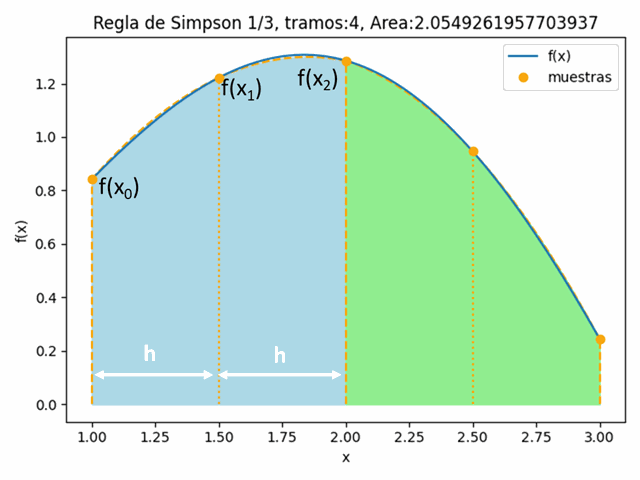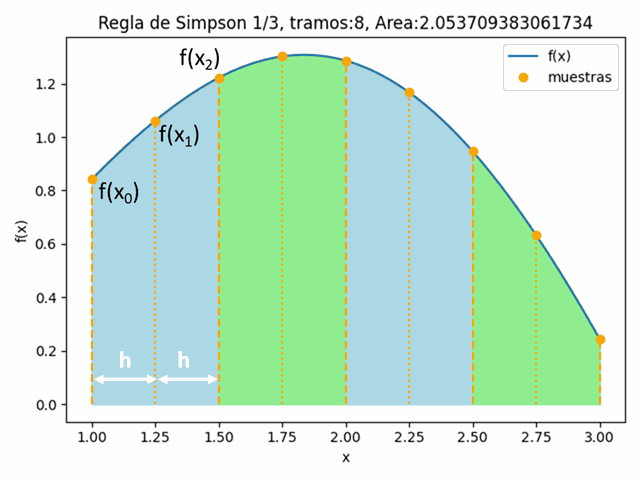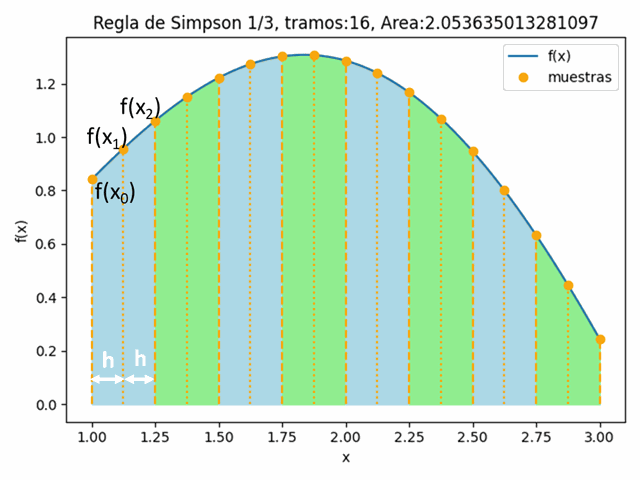

Es el resultado cuando se realiza una interpolación con polinomio de segundo grado.

I = \int_a^b f(x) \delta x \cong \int_a^b f_2 (x) \delta x

Se puede obtener usando un polinomio de Lagrange de segundo grado:

I = \int_{x_0}^{x_2} \bigg[ \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} f(x_0) +

+ \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} f(x_1) +

+ \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} f(x_2) \bigg] \delta x

que simplificando tiene como resultado para un solo tramo:

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)]

siendo h el tamaño de paso, donde para la expresión el divisor debe ser par, múltiplo de 2, al cubrir todo el intervalo [a,b]. En caso de usar valores de muestras xi, fi, el valor de h debe ser constante.

h=\frac{b-a}{tramos}

Error de truncamiento

la cota del error de truncamiento se estima como O(h⁵)

error_{trunca} = -\frac{h^5}{90} f^{(4)}(z)

para un valor de z dentro del intervalo [a,b] de integración.

para cuantificar el valor, se puede usar la diferencia finita Δ⁴f, pues con la derivada sería muy laborioso.

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]

2. Ejercicio

Para integrar la función en el intervalo [1,3] con 4, 16, 32 ,64 y 128 tramos,

f(x)= \sqrt {(x)} \sin(x)

1 \leq x \leq 3

Para el ejercicio planteado en la regla de trapecio, usando cuatro tramos, se aplica el método cada dos tramos.

tramos = 4

h = \frac{3-1}{4} = \frac{1}{2} = 0.5

I\cong \frac{0.5}{3}[f(1)+4f(1.5) + f(2)] +

+ \frac{0.5}{3}[f(2)+4f(2.5) + f(3)]

f(1)= \sqrt {(1)} \sin(1) = 0.8414

f(1.5)= \sqrt {(1.5)} \sin(1.5) = 1.2216

f(2)= \sqrt {(2)} \sin(2) = 1.2859

f(2.5)= \sqrt {(2.5)} \sin(2.5) = 0.9462

f(3)= \sqrt {(3)} \sin(3) = 0.2444

I\cong \frac{0.5}{3}[0.8414+4(1.2216) + 1.2859] +

+ \frac{0.5}{3}[1.2859+4(0.9462) + 0.2444]

I\cong 2.054

Note que al usar Simpson 1/3 con 4 tramos el resultado tiene los 2 primeros decimales iguales a usar Trapecio con 16 tramos.

>>> import numpy as np
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> xi = [1, 1+1/2, 1+2/2, 1+3/2,3]
>>> xi
[1, 1.5, 2.0, 2.5, 3]
>>> fx(xi)
array([0.84147098, 1.22167687, 1.28594075, 
       0.94626755, 0.24442702])
>>> (0.5/3)*(fx(1)+4*fx(1.5)+fx(2)) + (0.5/3)*(fx(2)+4*fx(2.5)+fx(3))
2.0549261957703937
>>>

Para más de 4 tramos es preferible realizar las operaciones con un algoritmo.

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

3. Algoritmo para integral f(x) en Python

Del ejercicio con trapecios, se repite el ejercicio con n tramos; usando dos tramos (tres puntos) en cada iteración.
Cada iteración se procesa avanzando dos puntos x_i, x_i+h, x_i+2h . Ejemplo:

tramos: 2
Integral fx con Simpson1/3:  2.0765536739078203

tramos: 4
Integral fx con Simpson1/3:  2.0549261957703937

tramos: 8
Integral fx con Simpson1/3:  2.053709383061734

tramos: 16
Integral fx con Simpson1/3:  2.053635013281097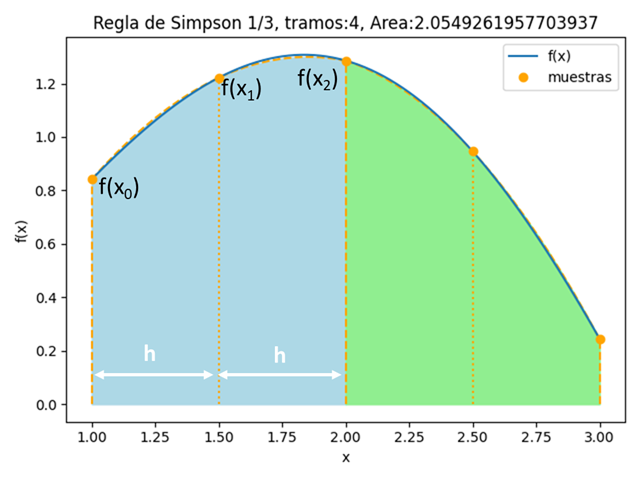

Se realiza mediante la aplicación directa de la fórmula para cada segmento conformado de dos tramos. Se verifica que el valor de tramos sea par.
Instrucciones en Python para f(x)

# Regla Simpson 1/3 para f(x) entre [a,b],tramos
import numpy as np

# INGRESO
fx = lambda x: np.sqrt(x)*np.sin(x)

a = 1 # intervalo de integración
b = 3
tramos = 2 # par, múltiplo de 2

# validar: tramos debe múltiplo de 2
while tramos%2 > 0: 
    print('tramos: ',tramos)
    tramos = int(input('tramos debe ser par: '))

# PROCEDIMIENTO
muestras = tramos + 1
xi = np.linspace(a,b,muestras)
fi = fx(xi)

# Regla de Simpson 1/3
h = (b-a)/tramos
suma = 0 # integral numérico
for i in range(0,tramos,2):
    S13= (h/3)*(fi[i]+4*fi[i+1]+fi[i+2])
    suma = suma + S13

# SALIDA
print('tramos:', tramos)
print('Integral fx con Simpson1/3: ', suma)

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

4. Gráfica para integral f(x) con Simpson 1/3

Se puede observar mejor lo expresado usando la gráfica para observar los tramos, muestras, por segmento. Para este caso se ejecuta el algoritmo anterior usando tramos=4.

Instrucciones en Python adicionales al algoritmo anterior

# GRAFICA ---------------------
import matplotlib.pyplot as plt

titulo = 'Regla de Simpson 1/3'
titulo = titulo + ', tramos:'+str(tramos)
titulo = titulo + ', Area:'+str(suma)

fx_existe = True
try: 
    # fx suave aumentando muestras
    muestrasfxSuave = tramos*10 + 1
    xk = np.linspace(a,b,muestrasfxSuave)
    fk = fx(xk)
except NameError:
    # falta variables a,b,muestras y la función fx
    fx_existe = False

try: # existen mensajes de error
    msj_existe = len(msj)
except NameError:
    # falta variables mensaje: msj
    msj = []  

# Simpson 1/3 relleno y bordes, cada 2 tramos
for i in range(0,muestras-1,2): 
    x_tramo = xi[i:(i+2)+1]
    f_tramo = fi[i:(i+2)+1]

    # interpolación polinomica a*(x**2)+b*x+c
    coef = np.polyfit(x_tramo, f_tramo, 2) # [a,b,c]
    px = lambda x: coef[0]*(x**2)+coef[1]*x+coef[2]

    xp = np.linspace(x_tramo[0],x_tramo[-1],21)
    fp = px(xp)
    
    plt.plot(xp,fp,linestyle='dashed',color='orange')
    
    relleno = 'lightgreen'
    if (i/2)%2==0: # bloque 2 tramos, es par
        relleno ='lightblue'
    if len(msj)==0: # sin errores
        plt.fill_between(xp,fp,fp*0,color=relleno)

# Divisiones verticales Simpson 1/3
for i in range(0,muestras,1):
    tipolinea = 'dotted'
    if i%2==0: # i par, multiplo de 2
        tipolinea = 'dashed'
    if len(msj)==0: # sin errores
        plt.vlines(xi[i],0,fi[i],linestyle=tipolinea,
                   color='orange')

# Graficar f(x), puntos
if fx_existe==True:
    plt.plot(xk,fk,label='f(x)')
plt.plot(xi,fi,'o',color='orange',label ='muestras')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title(titulo)
plt.legend()
plt.tight_layout()
plt.show()

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

5. Algoritmo para x[i], f[i] como muestras en Python

Cuando se integra sobre muestras dadas por los vectores xi, fi. Se revisa que los tramos entre muestras sean iguales para un Simpson 1/3 y que existan suficientes puntos para completar el integral.

xi = [1. , 1.5, 2. , 2.5, 3.]
fi = [0.84147098, 1.22167687, 1.28594075,
      0.94626755, 0.24442702]

Cuando se integra sobre muestras dadas por los vectores xi, fi. Se revisa que los tramos entre muestras sean iguales para un Simpson 1/3 y que existan suficientes puntos para completar el integral.

La gráfica se puede obtener usando el bloque correspondiente en la sección anterior.

# Integración Simpson 1/3 para muestras xi,fi
import numpy as np

# INGRESO
xi = [1. , 1.5, 2. , 2.5, 3.]
fi = [0.84147098, 1.22167687, 1.28594075,
      0.94626755, 0.24442702]

# PROCEDIMIENTO
casicero=1e-15
# vectores como arreglo, numeros reales
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
muestras = len(xi)
tramos = muestras-1

msj = [] # mensajes de error 
if tramos<2: # puntos insuficientes
    msj.append(['tramos insuficientes:',tramos])

suma = 0 # integral numerico
i = 0
while i<(muestras-2) and len(msj)==0: # i<tramos, al menos dos tramos
    h = xi[i+1]-xi[i] # tamaño de paso, supone constante
    if (i+2)<muestras: # dos tramos
        d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos
        errado = np.max(np.abs(d2x))
        if errado<casicero: # Simpson 1/3
            S13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2])
            suma = suma + S13
            i = i+2
        else:
            donde = np.argmax(np.abs(d2x))+i+1
            msj.append(['no equidistantes en i',donde])

# SALIDA
print('tramos: ',tramos)
if len(msj)>0: # mensajes de error
    print('Revisar errores en xi:',xi)
    print('tramos:',np.diff(xi,1))
    for unmsj in msj:
        print('',unmsj[0],':',unmsj[1])
else:
    print('Integral fx con Simpson1/3:',suma)

resultados

tramos:  4
Integral con Simpson 1/3:  2.0549261966666665
>>>

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..

6. Fórmula con varios segmentos y h constante

Usado cuando el intervalo a integrar tiene varios segmentos, cada segmento tiene dos tramos. Ejemplo para dos segmentos, cuatro tramos, semejante al usado en la gráfica. La simplificación es válida si h es constante.

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)] +

+ \frac{h}{3}[f(x_2)+4f(x_3) + f(x_4)]

tomando factor común h/3

I\cong \frac{h}{3}[f(x_0)+4f(x_1) + 2f(x_2) +

+4f(x_3) + f(x_4)]

[ Simpson 1/3 ] [ Ejercicio ] [ Algoritmo f(x) ] [ Algoritmo xi,fi ]
[ Integral Compuesto xi,fi ]