1.3 Polinomio de Taylor - Algoritmos101

1. Polinomio de Taylor - Serie de Taylor

La serie de Taylor proporciona un medio simplificar una función f(x) alrededor de punto x₀ de referencia mediante un polinomio. Los términos del polinomio p(x) se construyen con el valor de la función y sus derivadas en x₀.

P_{n}(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k

Cualquier función suave puede aproximarse por un polinomio. Como ejemplo, la expresión p(x) para cuatro términos de la serie es:

P_{n}(x) = f(x_0)+\frac{f'(x_0)}{1!} (x-x_0) +

+ \frac{f''(x_0)}{2!}(x-x_0)^2 +

+ \frac{f'''(x_0)}{3!}(x-x_0)^3 + \text{...}

Mientras más términos se añaden, la aproximación del polinomio p(x) se adapta más a f(x) en un mayor intervalo alrededor del punto de referencia x₀.

2. Ejercicio

Referencia: Burden 7Ed Capítulo 1.1 ejemplo 3 p11, 10Ed ejemplo 3 p8. Chapra, 4.1 p80. Taylor Series (Wikipedia)

Para la siguiente función trigonométrica f(x), alrededor de x₀=0, encontrar:

f(x) = \cos (x)

a) el segundo polinomio de Taylor (n=2),
b) el tercer polinomio de Taylor (n=3), para aproximar cos(0.01)
c) con el resultado anterior y su término residuo aproximar

\int_{0}^{0.1} \cos(x) dx

3. Desarrollo analítico

La expresión para los primeros términos del polinomio de Taylor de f(x) requiere determinar primera, segunda y tercera derivada:

P_{n}(x) = f(x_0)+\frac{f'(x_0)}{1!} (x-x_0) +

+ \frac{f''(x_0)}{2!}(x-x_0)^2 +

+ \frac{f'''(x_0)}{3!}(x-x_0)^3 + \text{...}

Se desarrollan las derivadas y se se evalúa cada expresión en x₀=0:

f(x) = cos(x)	f(0) = 1
f'(x) = -sen(x)	f'(0) = 0
f”(x) = -cos(x)	f”(0) = -1
f'”(x) = sen(x)	f’”(0) = 0
f⁴(x) = cos(x)	f⁴(0) = 1

Según el literal a del ejercicio, para n=2 y x₀=0:

\cos (x) = 1 + \frac{0}{1} (x-0) + \frac{-1}{2}(x-0)^2 +

+\frac{\sin(\xi(x))}{6}(x-0)^3

A la expresión se añade un término más para estimar el error, como residuo o error de truncamiento, evaluado en ξ(x).

\cos (x) = 1 - \frac{1}{2}x^2 + \frac{\sin(\xi(x))}{6}x^3

con lo que si x=0.01

\cos (0.01) = 1 - \frac{1}{2}(0.01)^2 + \frac{1}{6}(0.01)^3 \sin(\xi(x))

= 0.99995 + 0.16 \text{x} 10^{-6} \sin(\xi(x))

El término del error es es del orden 10^-6, la aproximación coincide por lo menos con los cinco primeros dígitos.

El residuo o error de truncamiento ξ(x) está entre 0 y x,

0<ξ(x) <0.01

Observe que los términos impares evaluados en x₀=0 se anulan, por lo que el polinomio solo cambia con términos pares.

Tarea: revisar y continuar con los siguientes literales.

4. Algoritmo con Sympy-Python

Una forma de obtener el polinomio de Taylor es crear una función que resuelva el polinomio. Por facilidad en el ejercicio, para obtener la expresión de las derivadas, se usan funciones matemáticas expresadas de forma simbólica con Sympy en Python.

De ser necesario, revise los conceptos sobre: Resumen Sympy – expresiones con símbolos

El algoritmo usa la forma simbólica de la expresión para crear el polinomio. La variable independiente x se establece como símbolo.

El procedimiento consiste en crear cada término k-ésimo y se añade a la expresión del polinomio. El términok se construye por partes, primero se obtiene la derivada, que luego se evalúa en derivadax0 y se incluye en la expresión del término. Se acumulan los términok y al final se presenta la expresión del polinomio

# Aproximación Polinomio de Taylor alrededor de x0
# f(x) en forma simbólica con Sympy
# Burden 7Ed Capítulo 1.1 Ejemplo 3.p11,pdf21;9Ed p11.

import numpy as np
import math
import sympy as sym

# INGRESO
x  = sym.Symbol('x') # variable independiente
fx = sym.cos(x)      # f(x) por aproximar
x0 = 0          # x0 de referencia o conocido
grado = 2       # grado>0
n  = grado + 1  # Términos de polinomio

# PROCEDIMIENTO
k = 0 # contador de términos
polinomio = 0
while (k < n):
    derivada   = fx.diff(x,k)
    derivadax0 = derivada.subs(x,x0)
    divisor   = math.factorial(k)
    terminok  = (derivadax0/divisor)*(x-x0)**k
    polinomio = polinomio + terminok
    k = k + 1

# SALIDA
print(polinomio)

Se usa un contador k de términos para el control de la construcción de la expresión final. Un ejemplo de ejecución del algoritmo con n=3:

1 - x**2/2

Se observa que el término 2do es cero. Para una interpretación gráfica del resultado, luego el polinomio se evalúa en el intervalo [a, b] que incluya x₀.

5. Algoritmo en Python como función

Puede reutilizar el algoritmo para el polinomio de Taylor presentado en el Ejercicio al convertirlo en una función de programación politaylor(). El procedimiento básico del algoritmo se agrega a una función def-return con el nombre politaylor() que entrega la expresión simbólica del polinomio p(x).

# Aproximación Polinomio de Taylor alrededor de x0
# f(x) en forma simbólica con Sympy

import numpy as np
import math
import sympy as sym

def politaylor(fx,x0,n):
    k = 0
    polinomio = 0
    while (k <= n):
        derivada   = fx.diff(x,k)
        derivadax0 = derivada.subs(x,x0)
        divisor   = math.factorial(k)
        terminok  = (derivadax0/divisor)*(x-x0)**k
        polinomio = polinomio + terminok
        k = k + 1
    return(polinomio)

# PROGRAMA  -------------
# Burden 7Ed Capítulo 1.1 Ejemplo 3.p11,pdf21;9Ed p11.

# INGRESO
x  = sym.Symbol('x') # variable independiente
fx = sym.cos(x)      # f(x) por aproximar
x0 = 0          # x0 de referencia o conocido
grado = 2       # grado>0
n  = grado + 1  # Términos de polinomio

# PROCEDIMIENTO
polinomio = politaylor(fx,x0,grado)

# SALIDA
print('grado:',grado)
print('polinomio:'+str(polinomio))

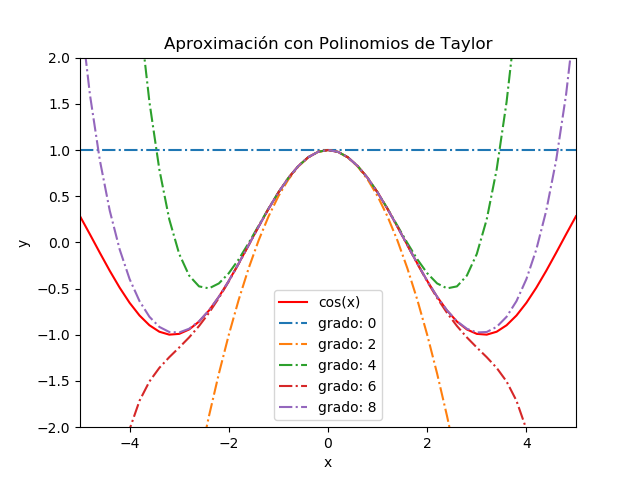
6. Gráfica de f(x) vs polinomio de Taylor

Para comparar los resultados, se procede a realizar la gráfica de f(x) vs el polinomio.

Esta es una sección complementaria para realizar la gráfica mostrada en el ejemplo. Requiere el uso de la librería matplotlib. Para más detalles, puede revisar la sección de Recursos/Resumen Python/Gráficas 2D de línea .

Para evaluar en el intervalo se requiere convertir las expresiones simbólicas a la forma numérica lambda: fxn, pxn
Para la gráfica, se usa el intervalo [a,b] con las muestras necesarias para una buena resolución de imagen. Se obtiene el vector xi
Se evalúa fxn y pxn en el intervalo, obteniendo los valores en los vectores: fi y pxi.
Se realiza la gráfica entre xi vs fi y pxi

# GRAFICA --------------------
import matplotlib.pyplot as plt

# intervalo de gráfica usando xi como referencia
a = - np.pi # izquierda
b = np.pi   # derecha
muestras = 21   # para la gráfica
titulo = 'Polinomio de Taylor para f(x)'

# Expresiones matemáticas símbolicas a numérica
fxn = sym.lambdify(x,fx,'numpy')
pxn = sym.lambdify(x,polinomio,'numpy')

# muestras para la gráfica
xi = np.linspace(a,b,muestras)
fi = fxn(xi)
pxi= pxn(xi)

# lineas en gráfica
plt.plot(xi,fi,label='f(x)')
plt.plot(xi,pxi,label='p(x)')

# entorno de gráfica
plt.xlabel('x')
plt.xlabel('y')
plt.title(titulo)
plt.legend()
plt.grid()
plt.show()

7. Función en librería Sympy.series

Sympy dispone de la función sym.series(fx,x,x0,n) para generar el polinomio de Taylor. La función tiene parámetros semejantes a los usados en los ejemplos anteriores y los algoritmos. Se muestra un ejemplo del uso de la función como referencia.

>>> import sympy as sym
>>> x = sym.Symbol('x')
>>> fx = sym.cos(x)
>>> polinomio = sym.series(fx,x,x0=0, n=3)
>>> polinomio
1 - x**2/2 + O(x**3)
>>>

El curso de métodos numéricos tiene mayor atención en los pasos o algoritmos que implementan los conceptos.

Los ejercicios desarrollan: primero, la parte la analítica/conceptual aplicadas a escribir con papel y lápiz, segundo, busca ejercitar habilidad de convertir los pasos usados en el papel a un algoritmo de computadora.

Con ambas partes, se busca ampliar así la capacidad de análisis e interpretación de resultados, errores de aproximación, convergencia, usando gráficas semejantes a la descrita en la siguiente página de la unidad.