[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
1. EDO \frac{\delta y}{\delta x} con Runge-Kutta de 2do Orden
Referencia: Burden 5.4 p209, Chapra 25.3 p740, Rodríguez 9.1.7 p354, Boyce DiPrima 4Ed 8.4 p450
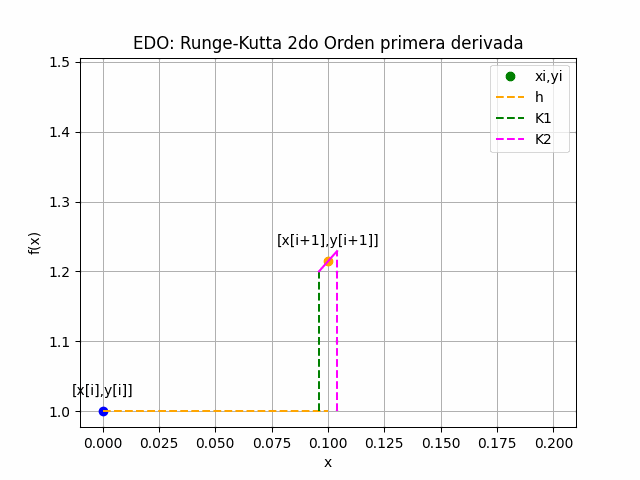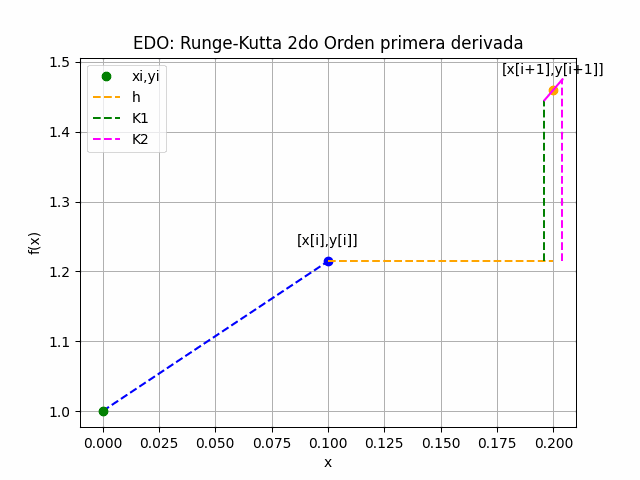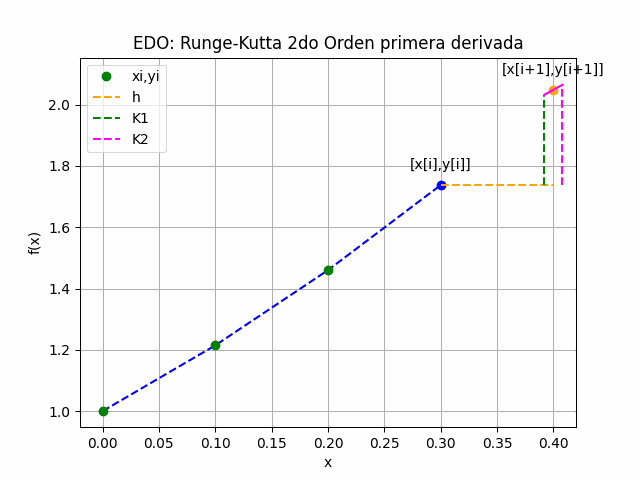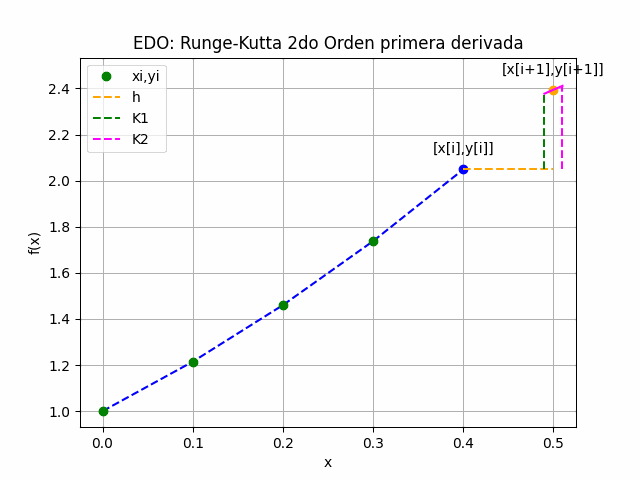
Para una ecuación diferencial ordinaria de primera derivada, el método Runge-Kutta de 2do Orden usa una corrección sobre la derivada a partir de los puntos xi y xi+h, es decir un tamaño de paso h hacia adelante, calculados como términos K1 y K2.
Considere una ecuación diferencial de primera derivada con una condición de inicio se reordena y se escribe como f(x,y) siguiendo los pasos:
Los términos K1 y K2 se calculan para predecir el próximo valor en y[i+1], observe que el término K1 es el mismo que el método de Edo con Taylor de dos términos.
K_1 = h f(x_i,y_i) K_2 = h f(x_i+h, y_i + K_1) y_{i+1} = y_i + \frac{K_1+K_2}{2} x_{i+1} = x_i + h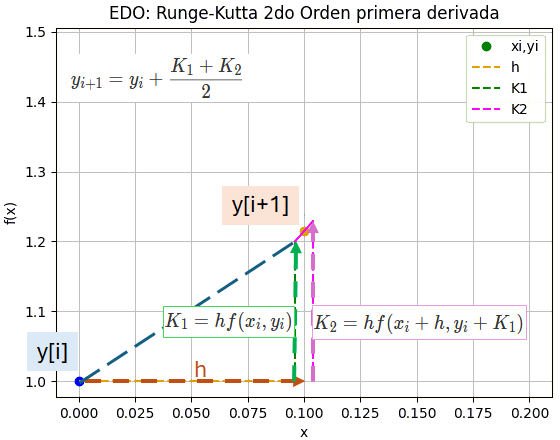
Runge-Kutta 2do Orden tiene error de truncamiento O(h3)
Las iteraciones se repiten para encontrar el siguiente punto en x[i+1] como se muestra en el gráfico animado.
Los métodos de Runge-Kutta mejoran la aproximación a la respuesta de la ecuación diferencial ordinaria sin requerir determinar las expresiones de las derivadas de orden superior, como fue necesario en EDO con Taylor.
Para observar al idea básica, considere observar un combate aéreo simulado en la década de 1940, donde las armas se encuentras fijas en las alas del avión. Observe dos minutos del video sugerido a partir de donde se encuentra marcado el enlace.
Video Revisar:
Luego de observar el video de introducción conteste las siguientes preguntas:
¿ Que trayectoria siguen los proyectiles al salir del cañón?
¿ Que trayectoria siguen los aviones, el perseguido y el que caza?
¿ Cuál es la relación entre las trayectorias de los dos aviones?
[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
2. Ejercicio
Referencia: Rodríguez 9.1.1 ejemplo p335. Chapra 25.1.3 p731
Se pide encontrar puntos de la solución en la ecuación diferencial usando los tres primeros términos de la serie de Taylor con h=0.1 y punto inicial x0=0, y0=1
\frac{dy}{dx}-y -x +x^2 -1 = 0 y'-y -x +x^2 -1 = 0[ Runge Kutta dy/dx] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
3. Desarrollo Analítico
Se reordena la expresión haciendo que la derivada se encuentre en el lado izquierdo:
f(x,y) = y' = y -x^2 +x +1Se usa las expresiones de Runge-Kutta en orden, K1 corresponde a una corrección de EDO con Taylor de dos términos (método de Euler). K2 considera el cálculo a un tamaño de paso más adelante. iteración:
K_1 = h f(x_i,y_i) = 0.1 (y_i -x_i^2 +x_i +1) K_2 = h f(x_i+h, y_i + K_1) K_2 = 0.1 \Big((y_i+K_1) -(x_i+h)^2 +(x_i+h) +1 \Big) y_{i+1} = y_i + \frac{K_1+K_2}{2} x_{i+1} = x_i + hRunge-Kutta 2do Orden tiene error de truncamiento O(h3)
para el ejercicio, el tamaño de paso h=0.1, se realizan tres iteraciones en las actividades del curso con lápiz y papel,
itera = 0 , x0 = 0, y0 = 1
K_1 = 0.1 f(0,1) = 0.1 \Big( 1 -0^2 +0 +1 \Big) = 0.2 K_2 = 0.1 f(0+0.1, 1+ 0.2) K_2 = 0.1 \Big( (1+ 0.2) - (0+0.1) ^2 +(0+0.1) +1\Big) = 0.229 y_1 = 1 + \frac{0.2+0.229}{2} = 1.2145 x_1 = 0 + 0.1 = 0.1itera = 1 , x1 = 0.1, y1 = 1.2145
K_1 = 0.1 f(0.1,1.2145) = 0.1( 1.2145 -0.1^2 +0.1 +1) K_1 = 0.2304 K_2 = 0.1 f(0.1+0.1, 1.2145 + 0.2304) =0.1 \Big((1.2145 + 0.2304) -(0.1+0.1)^2 +(0.1+0.1) +1\Big) K_2 = 0.2604 y_2 = 1.2145 + \frac{0.2304+0.2604}{2} = 1.4599 x_2 = 0.1 +0.1 = 0.2itera = 2 , x2 = 0.2, y2 = 1.4599
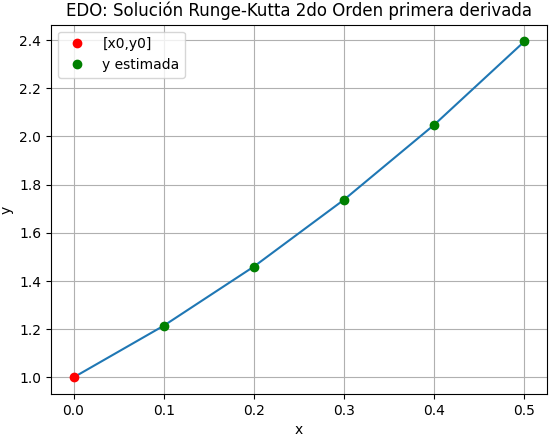
K_1 = 0.1 f(0.2,1.4599) = 0.1( 1.4599 -0.2^2 +0.2 +1) K_1 = 0.2619 K_2 = 0.1 f(0.2+0.1, 1.4599 + 0.2619) =0.1 \Big((1.4599 + 0.2619) -(0.2+0.1)^2 +(0.2+0.1) +1\Big) K_2 = 0.2931 y_2 = 1.4599 + \frac{0.2619+0.2931}{2} = 1.7375 x_2 = 0.2 +0.1 = 0.3luego de las 3 iteraciones en papel, se completan los demás puntos con el algoritmo obteniendo la gráfica resultante para y(x) correspondiente.
EDO dy/dx con Runge-Kutta 2 Orden i, [xi, yi, K1, K2] 0 [0. 1. 0. 0.] 1 [0.1 1.2145 0.2 0.229 ] 2 [0.2 1.459973 0.23045 0.260495] 3 [0.3 1.73757 0.261997 0.293197] 4 [0.4 2.048564 0.294757 0.327233] 5 [0.5 2.394364 0.328856 0.362742] >>>
Compare los resultados con Taylor de 2 y 3 términos.
Runge-Kutta 2do Orden tiene error de truncamiento O(h3)
[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
4. Algoritmo en Python
Para el ejercicio anterior, se adjunta el programa de prueba que usa la función rungekutta2(d1y,x0,y0,h,muestras) .
Las iteraciones y sus valores se pueden observar usando vertabla=true
# EDO dy/dx. M todo de RungeKutta 2do Orden # estima la solucion para muestras espaciadas h en eje x # valores iniciales x0,y0, entrega tabla[xi,yi,K1,K2] import numpy as np def rungekutta2(d1y,x0,y0,h,muestras, vertabla=False,precision=6): '''solucion a EDO dy/dx, con Runge Kutta de 2do orden d1y es la expresi n dy/dx, tambien planteada como f(x,y), valores iniciales: x0,y0, tama o de paso h. muestras es la cantidad de puntos a calcular. ''' tamano = muestras + 1 tabla = np.zeros(shape=(tamano,2+2),dtype=float) tabla[0] = [x0,y0,0,0] # incluye el punto [x0,y0] xi = x0 # valores iniciales yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (K1+K2)/2 xi = xi + h tabla[i] = [xi,yi,K1,K2] if vertabla==True: np.set_printoptions(precision) print( 'EDO dy/dx con Runge-Kutta 2 Orden') print('i, [xi, yi, K1, K2]') for i in range(0,tamano,1): print(i,tabla[i]) return(tabla) # PROGRAMA PRUEBA ------------------- # INGRESO # d1y = y' = f d1y = lambda x,y: y -x**2 + x + 1 x0 = 0 y0 = 1 h = 0.1 muestras = 5 # PROCEDIMIENTO tabla = rungekutta2(d1y,x0,y0,h,muestras, vertabla=True) xi = tabla[:,0] yiRK2 = tabla[:,1] # SALIDA #print(' [xi, yi, K1, K2]') #print(tabla) # GRAFICA import matplotlib.pyplot as plt plt.plot(xi,yiRK2) plt.plot(xi[0],yiRK2[0], 'o',color='r', label ='[x0,y0]') plt.plot(xi[1:],yiRK2[1:], 'o',color='m', label ='[xi,yi] Runge-Kutta') plt.title('EDO dy/dx: Runge-Kutta 2do Orden') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid() plt.show()
[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
5. Cálculo de Error con la solución conocida
La ecuación diferencial ordinaria del ejercicio tiene una solución conocida, lo que permite encontrar el error real en cada punto respecto a la aproximación estimada.
y = e^x + x + x^2
Note que el error crece al distanciarse del punto inicial.
Error máximo estimado: 0.004357584597315167 entre puntos: [0. 0.00067092 0.00143026 0.0022892 0.00326028 0.00435758] >>>
Para las siguientes instrucciones, comente la última línea #plt.show() antes de continuar con:
# ERROR vs solución conocida ----------------- y_sol = lambda x: ((np.e)**x) + x + x**2 yi_psol = y_sol(xi) errores = yi_psol - yiRK2 errormax = np.max(np.abs(errores)) # SALIDA print('Error máximo estimado: ',errormax) print('entre puntos: ') print(errores) # GRAFICA [a,b+2*h] a = x0 b = h*muestras+2*h muestreo = 10*muestras+2 xis = np.linspace(a,b,muestreo) yis = y_sol(xis) plt.plot(xis,yis, label='y solución conocida', linestyle='dashed') plt.legend() plt.show()
[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
6. Ejercicio de Evaluación
2Eva_IT2018_T1 EDO Paracaidista wingsuit
Solución Propuesta: s2Eva_IT2018_T1 EDO Paracaidista wingsuit , Runge-Rutta para primera derivada.