1ra Evaluación I Término 2010-2011. 6/Julio/2010. ICM02188. Métodos Numéricos
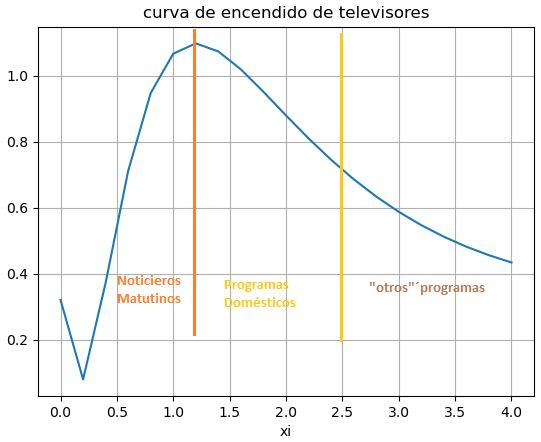
Tema 2. La curva de encendido de televisores en la ciudad de Guayaquil está en función de la hora del día y del día de la semana.

Suponga que en un intervalo de 4 horas, un determinado día , el porcentaje de televisores encendidos está dado por la función:
p(x) =\frac{1}{2.5} \left(-10 \sin \left(\frac{12x}{7} \right) e^{-\frac{24x}{7}} + \frac{48x}{7}e^{-\frac{8x}{7}} + 0.8 \right)0≤x≤4
x: Tiempo en horas
p: porcentaje en horas de televisores encendidos
a. Encuentre un intervalo en que se encuentre el máximo de la función p
b. Utilice el método de Newton-Raphson para encontrar el máximo de la función p. Calcule la respuesta con un error máximo de 0.0001
c. Encuentre el mínimo de la función p en el mismo intervalo de cuatro horas con el mismo método y con la misma precisión anteriores.
Gráfica de referencia