4.2 Diferencias finitas, tabla con Python

1. Diferencias finitas

Referencia: Rodríguez 6.5 p211, Chapra 18.1.3 p509

Establece relaciones simples entre los puntos dados que describen la función f(x). Las tabla de diferencias finitas es un elemento base para varios métodos de interpolación, por lo que se trata como un tema inicial.

2. Ejercicio

Los datos provienen del ejercicio para el polinomio de interpolación con Vandermonde. Se modifica el primer par ordenado a [0.1, 1.45].

xi = [0.1, 0.2, 0.3, 0.4] 
fi = [1.45, 1.6, 1.7, 2.0]

x_i	0.1	0.2	0.3	0.4
f_i	1.45	1.6	1.7	2.0

3. Desarrollo analítico

La tabla de diferencias finitas se construye tomando los datos y sus índices como parte de las primeras columnas.

i	x_i	f_i	Δ¹f_i	Δ²f_i	Δ³f_i	Δ⁴f_i
0	0.1	1.45	0.15	-0.05	0.25	0.
1	0.2	1.6	0.1	0.2	0.	0.
2	0.3	1.7	0.3	0.	0.	0.
3	0.4	2.0	0.	0.	0.	0.

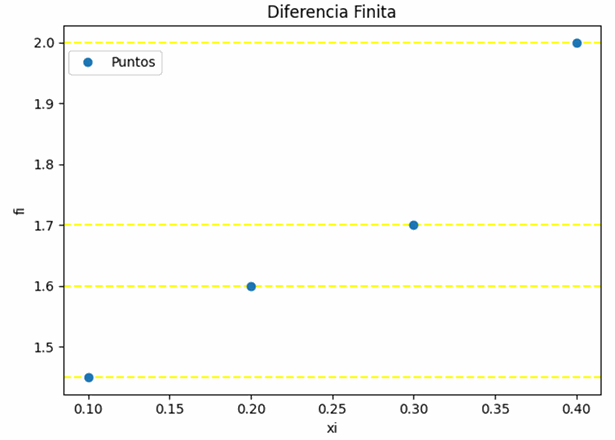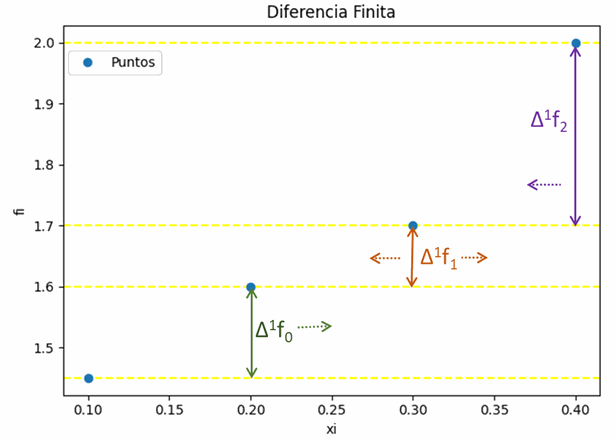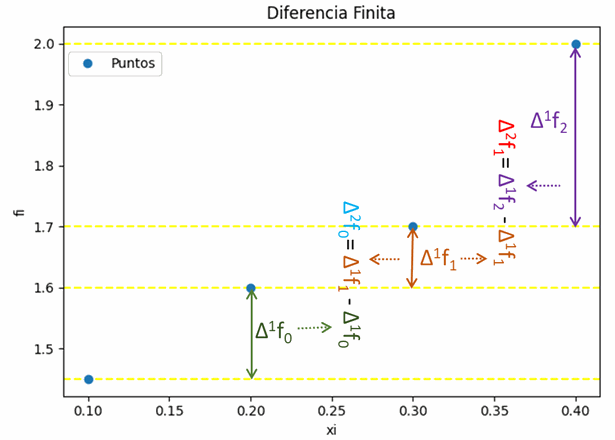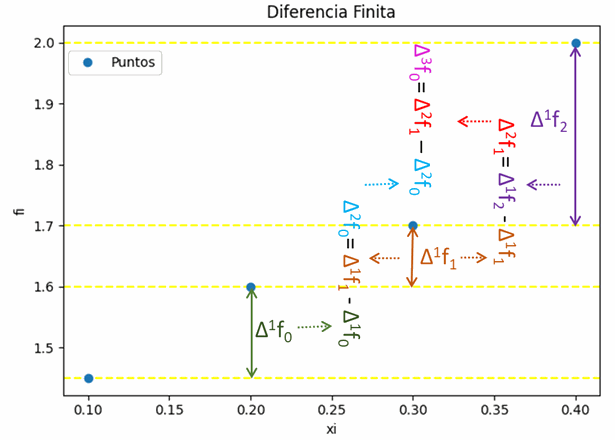
Cada casilla de diferencia finita Δ^jf_i se obtiene restando los dos valores consecutivos de la columna anterior. Por ejemplo, para la primera columna:

\Delta ^1 f_0 = 1.6-1.45 = 0.15

\Delta ^1 f_1 = 1.7-1.6 = 0.1

\Delta ^1 f_2 = 2.0-1.7 = 0.3

y la siguiente Δ¹f₃ no es posible calcular.

Siguiendo el mismo procedimiento se calculan los valores de la siguiente columna Δ²f_i como las diferencias de la columna anterior.

\Delta ^2 f_0 = 0.1-0.15 = -0.05

\Delta ^2 f_1 = 0.3-0.1 = 0.2

finalmente Δ³f_i

\Delta ^3 f_0 = 0.2-(-0.05) = 0.25

Si la función f(x) de donde provienen los datos es un polinomio de grado n, entonces la n-ésima diferencia finita será una constante, y las siguientes diferencias se anularán.

4. Algoritmo en Python

Para crear la tabla de diferencias finitas, las primeras columnas requieren concatenar los valores de los índices i, xi y fi.

xi = [0.10, 0.2, 0.3, 0.4]
fi = [1.45, 1.6, 1.7, 2.0]

Los índices i se crean en un vector ki, pues la variable i es usada como fila en matrices, por lo que evitamos confundirlas al usar la variable.

A la matriz con las tres columnas descritas, se le añade a la derecha una matriz de nxn para calcular las diferencias.

Se calculan las diferencias para cada columna, realizando la operación entre los valores de cada fila. Considere que no se realizan cálculos desde la diagonal hacia abajo en la tabla, los valores quedan como cero.

Al final se muestra el título y el resultado de la tabla.

# Diferencias finitas: [tabla_etiq,tabla]
# Tarea: verificar tamaño de vectores
import numpy as np

# INGRESO, Datos de prueba
xi = [0.10, 0.2, 0.3, 0.4]
fi = [1.45, 1.6, 1.7, 2.0]

# PROCEDIMIENTO
casicero = 1e-15  # redondear a cero
# Matrices como arreglo, numeros reales
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
n = len(xi)

# Tabla de Diferencias Finitas
tabla_etiq = ['i','xi','fi']
ki = np.arange(0,n,1) # filas
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)
n,m = np.shape(tabla)
# Calular tabla de Diferencias Finitas
diagonal = n-1 # derecha a izquierda
j = 3  # inicia en columna 3
while (j < m): # columna
    tabla_etiq.append('d'+str(j-2)+'f') 
    i = 0 # fila
    while (i < diagonal): # antes de diagonal
        tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1]
        
        if abs(tabla[i,j])<casicero: # casicero revisa
                tabla[i,j]=0
        i = i + 1
    diagonal = diagonal - 1
    j = j + 1

# SALIDA
print('Tabla Diferencia Finita: ')
print([tabla_etiq])
print(tabla)

el resultado de aplicar el algoritmo es:

Tabla Diferencia Finita: 
[['i', 'xi', 'fi', 'd1f', 'd2f', 'd3f', 'd4f']]
[[ 0.    0.1   1.45  0.15 -0.05  0.25  0.  ]
 [ 1.    0.2   1.6   0.1   0.2   0.    0.  ]
 [ 2.    0.3   1.7   0.3   0.    0.    0.  ]
 [ 3.    0.4   2.    0.    0.    0.    0.  ]]
>>>

5. Gráfica de puntos con líneas horizontales

Para tener una referencia visual sobre las primeras diferencias finitas, en una gráfica se trazan las líneas horizontales que pasan por cada punto. Para las segundas diferencias se debe incluir en la gráfica las primeras diferencias finitas vs xi repitiendo el proceso. Las líneas de distancia se añadieron con un editor de imágenes.

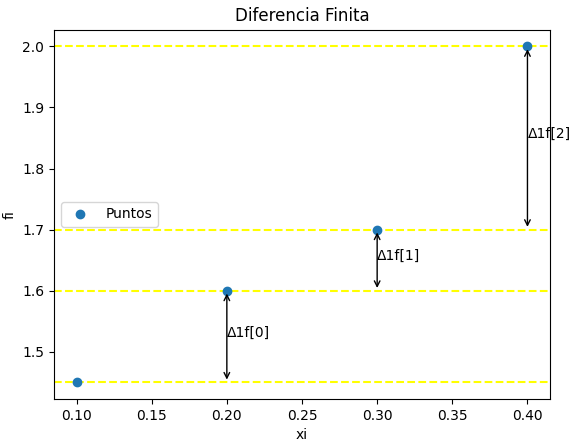
Las instrucciones adicionales al algoritmo anterior para añadir la gráfica son:

# Gráfica --------------
import matplotlib.pyplot as plt

titulo = 'Diferencia Finita'

for i in range(0,n,1):
    plt.axhline(fi[i],ls='--', color='yellow')
    if i<(n-1):
        plt.annotate("", xytext=(xi[i+1], fi[i]),
                     xy=(xi[i+1], fi[i+1]),
                     arrowprops=dict(arrowstyle="<->"),
                     color='magenta')
        plt.annotate("Δ1f["+str(i)+"]",
                     xy=(xi[i+1], fi[i+1]),
                     xytext=(xi[i+1],(fi[i]+fi[i+1])/2))
                     
plt.plot(xi,fi,'o', label = 'Puntos')
plt.legend()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title(titulo)
plt.show()

6. Diferencias finitas en librería Numpy.diff

np.diff(vector,orden)calcula la diferencia de elementos consecutivos a lo largo de un eje específico de una matriz. Incluye un parámetro de orden para la n-esima diferencia finita. Ejemplo:

>>> import numpy as np
>>> xi = [0.10, 0.2, 0.3, 0.4]
>>> fi = [1.45, 1.6, 1.7, 2.0]
>>> d1f = np.diff(fi,1)
>>> d1f
array([0.15, 0.1 , 0.3 ])
>>> d2f = np.diff(fi,2)
>>> d2f
array([-0.05,  0.2 ])
>>> d1x = np.diff(xi,1)
>>> d1x
array([0.1, 0.1, 0.1])
>>> d2x = np.diff(xi,n=2)
>>> d2x
array([-2.77555756e-17,  5.55111512e-17])

Δ²x_i es un valor casicero que se debe incluir en el algoritmo para redondear a cero cuando sea por ejemplo 10^-15. Asunto que ya fue incluido desde Método de Gauss en la unidad de sistemas de ecuaciones

Referencia: https://numpy.org/doc/stable/reference/generated/numpy.diff.html