Ejercicio: 1Eva2019TII_T2 Proceso Termodinámico
la ecuación para el problema se describe como:
f(x)=e^{-0.5x}ecuación que se usa para describir los siguientes puntos:
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| f(x) | 1 | 0.60653065 | 0.36787944 | 0.22313016 | 0.13533528 |
Como el polinomio es de grado 2, se utilizan tres puntos. Para cubrir el intervalo los puntos seleccionados incluyen los extremos y el punto medio.
literal a
Con los puntos seleccionados se escriben las ecuaciones del polinomio:
p_2(x)= a_0 x^2 + a_1 x + a_2usando los valores de la tabla:
p_2(0)=a_0 (0)^2 + a_1 (0) + a_2 = 1 p_2(2)=a_0 (2)^2 + a_1 (2) + a_2 = 0.36787944 p_2(4)=a_0 (4)^2 + a_1 (4) + a_2 = 0.13533528con la que se escribe la matriz Vandermonde con la forma A.x=B
A= [[ 0., 0., 1.,]
[ 4., 2., 1.,]
[16., 4., 1.,]]
B= [[1. ],
[0.36787944],
[0.13533528]]) matriz aumentada
[[ 0., 0., 1., 1. ]
[ 4., 2., 1., 0.36787944]
[16., 4., 1., 0.13533528]]matriz pivoteada
[[16., 4., 1., 0.13533528]
[ 4., 2., 1., 0.36787944]
[ 0., 0., 1., 1. ]]Resolviendo por algún método directo, la solución proporciona los coeficientes del polinomio
Tarea: escribir la solución del método directo, semejante a la presentada en el tema 3
[ 0.04994705 -0.41595438 1. ]con lo que el polinomio de interpolación es:
p_2(x) = 0.04994705 x^2 - 0.41595438 x + 1.0en el enunciado se requiere la evaluación en x=2.4
p_2(2.4) = 0.04994705 (2.4)^2 - 0.41595438 (2.4) + 1.0 f(2.4)=e^{-0.5(2.4)} error = |f(2.4)-p_2(2.4)|Evaluando en X1: 2.4
Evaluando p(x1): 0.2894044975129779
Error en x1: 0.011789714399224216
Error relativo: 0.039143230291095066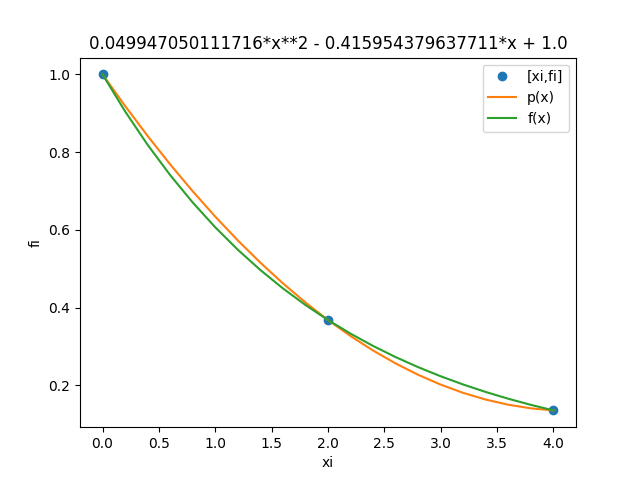
La diferencia entre la función y el polinomio de interpolación se puede observar en la gráfica:
literal b
Tarea: Encontrar la cota de error con f(1.7)
Algoritmo en Python
Resultado con el algoritmo
Matriz Vandermonde:
[[ 0. 0. 1.]
[ 4. 2. 1.]
[16. 4. 1.]]
los coeficientes del polinomio:
[ 0.04994705 -0.41595438 1. ]
Polinomio de interpolación:
0.049947050111716*x**2 - 0.415954379637711*x + 1.0
formato pprint
2
0.049947050111716*x - 0.415954379637711*x + 1.0
Evaluando en X1: 2.4
Evaluando p(x1): 0.2894044975129779
Error en x1: 0.011789714399224216
Error relativo: 0.039143230291095066
Evaluando en X2: 1.7
Evaluando p(x2): 0.2894044975129779
Error en x2: 0.011789714399224216
Error relativo: 0.039143230291095066
Presentado por secciones, semejante a lo desarrollado en clases
# 1Eva_IIT2019_T2 Proceso Termodinámico
# El polinomio de interpolación
import numpy as np
import sympy as sym
# INGRESO
fx = lambda x: np.exp(-0.5*x)
xi =np.array([0,2,4],dtype=float)
# determina vector
fi= fx(xi)
# PROCEDIMIENTO
# Convierte a arreglos numpy
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
B = fi
n = len(xi)
# Matriz Vandermonde D
D = np.zeros(shape=(n,n),dtype=float)
for i in range(0,n,1):
for j in range(0,n,1):
potencia = (n-1)-j # Derecha a izquierda
D[i,j] = xi[i]**potencia
# Aplicar métodos Unidad03. Tarea
# Resuelve sistema de ecuaciones A.X=B
coeficiente = np.linalg.solve(D,B)
# Polinomio en forma simbólica
x = sym.Symbol('x')
polinomio = 0
for i in range(0,n,1):
potencia = (n-1)-i # Derecha a izquierda
termino = coeficiente[i]*(x**potencia)
polinomio = polinomio + termino
# Polinomio a forma Lambda x:
# para evaluación con vectores de datos xin
muestras = 21
px = sym.lambdify(x,polinomio)
# SALIDA
print('Matriz Vandermonde: ')
print(D)
print('los coeficientes del polinomio: ')
print(coeficiente)
print('Polinomio de interpolación: ')
print(polinomio)
print('\n formato pprint')
sym.pprint(polinomio)
# literal b
x1 = 2.4
px1 = px(x1)
fx1 = fx(x1)
errorx1 = np.abs(px1-fx1)
errorx1rel = errorx1/fx1
x2 = 1.7
px2 = px(x1)
fx2 = fx(x1)
errorx2 = np.abs(px1-fx1)
errorx2rel = errorx1/fx1
print()
print('Evaluando en X1: ',x1)
print('Evaluando p(x1): ',px1)
print('Error en x1: ',errorx1)
print(' Error relativo: ', errorx1rel)
print()
print('Evaluando en X2: ',x2)
print('Evaluando p(x2): ',px2)
print('Error en x2: ',errorx2)
print(' Error relativo: ', errorx2rel)
# GRAFICA
import matplotlib.pyplot as plt
a = np.min(xi)
b = np.max(xi)
xin = np.linspace(a,b,muestras)
yin = px(xin)
# Usando evaluación simbólica
##yin = np.zeros(muestras,dtype=float)
##for j in range(0,muestras,1):
## yin[j] = polinomio.subs(x,xin[j])
plt.plot(xi,fi,'o', label='[xi,fi]')
plt.plot(xin,yin, label='p(x)')
plt.plot(xin,fx(xin), label='f(x)')
plt.xlabel('xi')
plt.ylabel('fi')
plt.legend()
plt.title(polinomio)
plt.show()