Ejercicio: 1Eva_2025PAOI_T1 Recargar combustible en órbita

literal a. Planteamiento

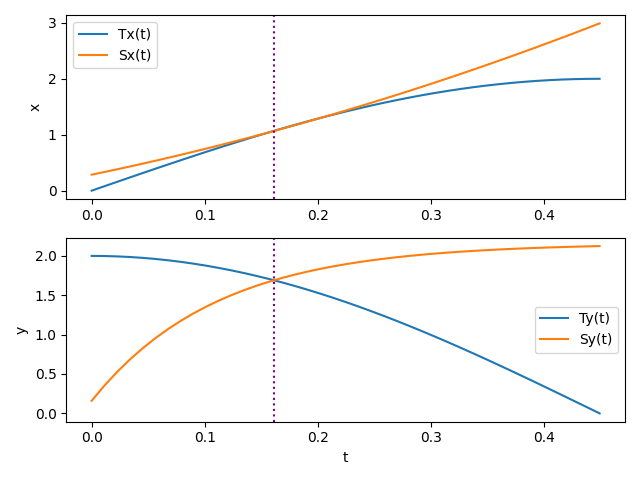
Según el enunciado, se plantea el ejercicio primero para el eje y. Cuando las coordenadas de ambos son iguales en el eje y.

T_y (t) = 2\cos(3.5t) S_y (t) = 2 - 2e^{(-9t)} T_y (t) = S_y (t) 2\cos(3.5t) =2 - 2e^{(-9t)} 2 - 2e^{(-9t)} -2\cos(3.5t) = 0 f(t) = 2 - 2e^{(-9t)} -2\cos(3.5t)

literal b. Intervalo [a,b]

Las gráficas presentadas en el enunciado, confirman que existe una raíz en el intervalo 0 ≤ t ≤ (π/7). Se verifica revisando el signo de f(t) en los extremos del intervalo:

f(0) = 2 - 2e^{(-9(0))} -2\cos(3.5(0)) =-2 f(π/7) = 2 - 2e^{(-9(π/7))} -2\cos(3.5(π/7))=1.9647

Los resultados tienen signos opuestos, lo que confirma que existe al menos una raíz en el intervalo.

literal c. Método de Newton-Raphson

En éste método se requiere de la derivada f'(t)

f(t) = 2 - 2e^{(-9t)} -2\cos(3.5t) f'(t) = 18e^{(-9t)} +2(3.5)\sin(3.5t)

import sympy as sym
t = sym.Symbol('t')
f = 2-2*sym.exp(-9*t)-2*sym.cos(3.5*t)
df = sym.diff(f,t,1)
print(df)

resultado:

7.0*sin(3.5*t) + 18*exp(-9*t)

itera = 0

el punto inicial de búsqueda puede ser x₀=0.1, que se encuentra dentro del intervalo

f(0.1) = 2 - 2e^{(-9(0.1))} -2\cos(3.5(0.1)) = -0.6918 f'(0.1) = 18e^{(-9(0.1))} +2(3.5)\sin(3.5(0.1)) = 9.7185 x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 0.1 - \frac{-0.6918}{9.7185} =0.1711 tramo = |0.1711-0.1| = 0.0711

itera = 1

x₁= 0.1711

f(0.1711) = 2 -2e^{(-9(0.1711))} -2\cos(3.5(0.1711)) =-0.08005 f'(0.1711) = 18e^{(-9(0.1711))} + 2(3.5)\sin(3.5(0.1711))=7.8037 x_1 = 0.1711 - \frac{-0.08005}{7.8037} =0.1814 tramo = |0.1814-0.1711| = 0.0102

itera = 2
x₂= 0.1814

f(0.1814) = 2 -2e^{(-9(0.1814))} -2\cos(3.5(0.1814)) =-0.0003660 f'(0.1814) = 18e^{(-9(0.1814))} + 2(3.5)\sin(3.5(0.1814)) =7.9654 x_1 = 0.1814 - \frac{-0.0003660}{7.9654} = 0.1815 tramo = |0.1815-0.1814| = 0.0001

literal d y e. Errores por iteración

En el desarrollo se muestran los errores como tramos. Se observa que los errores disminuyen en cada iteración, por lo que se considera que el método converge.  El error de la última iteración es del orden de 10^-4, lo que es menor que la  tolerancia 10^-3. por lo que la raíz será: 0.1815

Nota: el algoritmo lo obtiene del blog y lo modifica para el ejercicio, obteniendo los datos de las operaciones

Resultados con el algoritmo:

i: 1 fi: -0.691884745175956 dfi: 9.718538527518945
   xnuevo: 0.171192262418554 tramo: 0.071192262418554
i: 2 fi: -0.08005384152091866 dfi: 7.803760114465353
   xnuevo: 0.18145063022416194 tramo: 0.010258367805607932
i: 3 fi: -0.0007153774553945169 dfi: 7.668649926460424
   xnuevo: 0.18154391619525917 tramo: 9.328597109722891e-05
raiz en:  0.18154391619525917
con error de:  9.328597109722891e-05

Gráfica f(t) = Sy(t) - Ty(t)

---

literal f. Encontrar k en Sx(t) = Tx(t)

Se usan las ecuaciones en eje x con el valor encontrado t=0.1815.

No se indica desarrollar el ejercicio en papel y lápiz, por lo que la respuesta es solo con el algoritmo, por ejemplo, bisección.

T_x (t) = 2\sin(3.5t) S_x (t) = 3.2(t+k)+4.1(t+k)^2 T_x (t) = S_x (t) 2\sin(3.5t) = 3.2(t+k)+4.1(t+k)^2 3.2(t+k)+4.1(t+k)^2-2\sin(3.5t) =0 3.2(0.1815+k)+4.1(0.1815+k)^2 -2\sin(3.5(0.1815))=0 f(k) = 3.2(0.1815+k)+4.1(0.1815+k)^2 - 2\sin(3.5(0.1815))

que da una función dependiente de k, usando el método de la bisección, para el intervalo [0,π/7] y tolerancia del ejercicio anterior, siempre que exista cambio de signo se prueba:

i: 0 a: 0 c: 0.2243994752564138 b: 0.4487989505128276
  fa: -0.4709358324617918 fc: 0.7876530469374095 fb: 2.459153947198512 tramo: 0.2243994752564138
i: 1 a: 0 c: 0.1121997376282069 b: 0.2243994752564138
  fa: -0.4709358324617918 fc: 0.10674460463007107 fb: 0.7876530469374095 tramo: 0.1121997376282069
i: 2 a: 0 c: 0.05609986881410345 b: 0.1121997376282069
  fa: -0.4709358324617918 fc: -0.19499911456779484 fb: 0.10674460463007107 tramo: 0.05609986881410345
i: 3 a: 0.05609986881410345 c: 0.08414980322115517 b: 0.1121997376282069
  fa: -0.19499911456779484 fc: -0.0473531301318455 fb: 0.10674460463007107 tramo: 0.028049934407051724
i: 4 a: 0.08414980322115517 c: 0.09817477042468103 b: 0.1121997376282069
  fa: -0.0473531301318455 fc: 0.028889268458366812 fb: 0.10674460463007107 tramo: 0.014024967203525862
i: 5 a: 0.08414980322115517 c: 0.0911622868229181 b: 0.09817477042468103
  fa: -0.0473531301318455 fc: -0.009433548034425865 fb: 0.028889268458366812 tramo: 0.007012483601762931
i: 6 a: 0.0911622868229181 c: 0.09466852862379957 b: 0.09817477042468103
  fa: -0.009433548034425865 fc: 0.00967745591254876 fb: 0.028889268458366812 tramo: 0.0035062418008814655
i: 7 a: 0.0911622868229181 c: 0.09291540772335884 b: 0.09466852862379957
  fa: -0.009433548034425865 fc: 0.00010935286420599155 fb: 0.00967745591254876 tramo: 0.0017531209004407328
i: 8 a: 0.0911622868229181 c: 0.09203884727313846 b: 0.09291540772335884
  fa: -0.009433548034425865 fc: -0.0046652478538238285 fb: 0.00010935286420599155 tramo: 0.0008765604502203733
       raiz en:  0.09203884727313846
error en tramo:  0.0008765604502203733

se encuentra k = 0.09203