Ejercicio: 1Eva2025PAOII_T1 Trayectoria cometa y planeta

literal a

Plantear el ejercicio para la intersección de trayectorias.

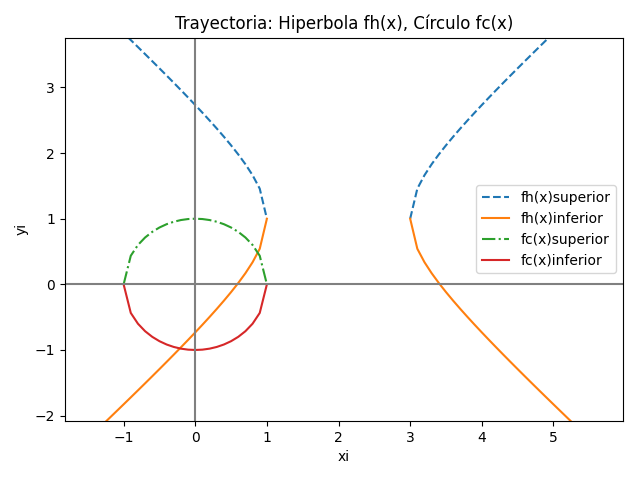
Trayectoria hipérbola / cometa

\dfrac{(x-x_h )^2}{a_h^2}-\dfrac{(y-y_h )^2}{b_h^2}=1

x_h = 2, y_h = 1, a_h = 1, b_h = 1

sustituyendo los valores conocidos,

\dfrac{(x-2 )^2}{1^2} -\dfrac{(y-1)^2}{1^2} =1 (x-2 )^2 - (y-1)^2 =1

despejar la variable y,

(x-2 )^2 - 1 =(y-1)^2 \sqrt{(x-2 )^2 - 1} =\sqrt{(y-1)^2} \sqrt{(x-2 )^2 - 1} =y-1 y = \pm \sqrt{(x-2 )^2 - 1} +1

Trayectoria del círculo / planeta

(x-x_c )^2+(y-y_c )^2=1

x_c = 0, y_c = 0

sustituye valores conocidos

(x-0 )^2+(y-0 )^2=1 x^2+y^2=1 y^2 = 1 - x^2 \sqrt{y^2} =\sqrt{ 1 - x^2} y =\pm \sqrt{ 1 - x^2}

La expresión tiene una parte positiva y otra negativa en ambos casos.

literal b

Indique y verifique el intervalo [a,b] de la intersección.

Según la gráfica presentada en el enunciado, para la hipérbola se toma la parte inferior:

y = -\sqrt{(x-2 )^2 - 1} +1

En el caso del círculo si es la parte superior, el intervalo x estaría entre [0,1]

y =\sqrt{ 1 - x^2}

En el caso del círculo si es la parte inferior, el intervalo x estaría entre [-1,0]

y =- \sqrt{ 1 - x^2}

tomando la parte superior del círculo, se igualan y de cada ecuación.

-\sqrt{(x-2 )^2 - 1} +1 = + \sqrt{ 1 - x^2} \sqrt{ 1 - x^2}+\sqrt{(x-2 )^2 - 1} -1 = 0 f(x) = \sqrt{ 1 - x^2}+\sqrt{(x-2 )^2 - 1} -1

literal c y d

Desarrolle con el método de la bisección

itera = 0, a = 0, b=1

f(0) = \sqrt{ 1 - 0^2}+\sqrt{(0-2 )^2 - 1} -1 = 1.7321 f(1) = \sqrt{ 1 - 1^2}+\sqrt{(1-2 )^2 - 1} -1 =-1

hay cambio de signo, el intervalo es válido

c=\frac{a+b}{2}=\frac{0+1}{2} = 0.5 f(0.5) = \sqrt{ 1 - 0.5^2}+\sqrt{(0.5-2 )^2 - 1} -1 = 0.9841

Hay cambio de signo del lado derecho,

a= 0.5, b=1

errado = |b-a| =|1-0.5| =0.5

itera = 1

c=\frac{0.5+1}{2}=0.75 f(0.75) = \sqrt{ 1 - 0.75^2}+\sqrt{(0.75-2 )^2 - 1} -1 = 0.4114

Hay cambio de signo del lado derecho,

a= 0.75, b=1

errado = |b-a| =|1-0.75| =0.25

itera = 2

c=\frac{0.75+1}{2}=0.875 f(0.875) = \sqrt{ 1 - 0.875^2}+\sqrt{(0.875-2 )^2 - 1} -1 = -0.0004888

Hay cambio de signo del lado izquierdo,

a= 0.75, b=0.875

errado = |b-a| =|0.875-0.75| =0.125

literal e

El error disminuye en cada iteración, por lo que se estima que el método converge. Se comprueba con los resultados del algoritmo.

literal f

método de Bisección
i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)']
   tramo
0 [0.  0.5 1. ] [ 1.7321  0.9841 -1.    ]
   0.5
1 [0.5  0.75 1.  ] [ 0.9841  0.4114 -1.    ]
   0.25
2 [0.75  0.875 1.   ] [ 4.1144e-01 -4.8888e-04 -1.0000e+00]
   0.125
3 [0.75   0.8125 0.875 ] [ 0.4114  0.2234 -0.0005]
   0.0625
4 [0.8125 0.8438 0.875 ] [ 0.2234  0.1172 -0.0005]
   0.03125
5 [0.8438 0.8594 0.875 ] [ 0.1172  0.06   -0.0005]
   0.015625
6 [0.8594 0.8672 0.875 ] [ 0.06    0.0302 -0.0005]
   0.0078125
7 [0.8672 0.8711 0.875 ] [ 0.0302  0.015  -0.0005]
   0.00390625
8 [0.8711 0.873  0.875 ] [ 0.015   0.0073 -0.0005]
   0.001953125
9 [0.873 0.874 0.875] [ 0.0073  0.0034 -0.0005]
   0.0009765625
raíz en:  0.8740234375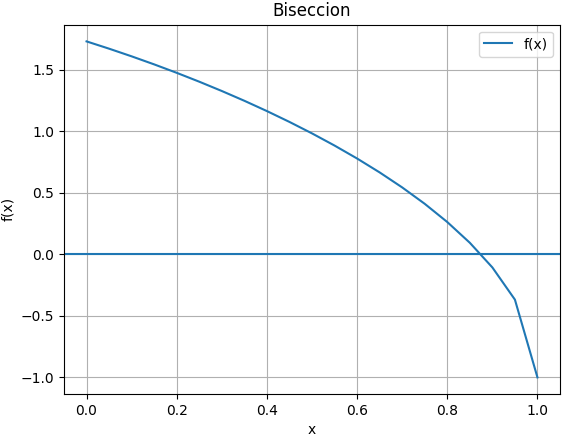

instrucciones en Python

# 1Eva2025PAOII_T1 Trayectoria cometa y planeta
# Algoritmo de Bisección
# [a,b] se escogen de la gráfica de la función
# error = tolera
import numpy as np
 
def biseccion(fx,a,b,tolera,iteramax = 50, vertabla=False, precision=4):
    '''
    Algoritmo de Bisección
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    error = tolera
    '''
    fa = fx(a)
    fb = fx(b)
    tramo = np.abs(b-a)
    itera = 0
    cambia = np.sign(fa)*np.sign(fb)
    if cambia<0: # existe cambio de signo f(a) vs f(b)
        if vertabla==True:
            print('método de Bisección')
            print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
            print('  ','tramo')
            np.set_printoptions(precision)
 
        while (tramo>=tolera and itera<=iteramax):
            c = (a+b)/2
            fc = fx(c)
            cambia = np.sign(fa)*np.sign(fc)
            if vertabla==True:
                print(itera,np.array([a,c,b]),
                      np.array([fa,fc,fb]))
            if (cambia<0):
                b = c
                fb = fc
            else:
                a = c
                fa = fc
            tramo = np.abs(b-a)
            if vertabla==True:
                print('  ',tramo)
            itera = itera + 1
        respuesta = c
        # Valida respuesta
        if (itera>=iteramax):
            respuesta = np.nan
 
    else: 
        print(' No existe cambio de signo entre f(a) y f(b)')
        print(' f(a) =',fa,',  f(b) =',fb) 
        respuesta=np.nan
    return(respuesta)
 
# PROGRAMA ----------------------
# INGRESO
fx = lambda x: np.sqrt(1-x**2)+np.sqrt((x-2)**2-1)- 1
a = 0
b = 1
tolera = 0.001
 
# PROCEDIMIENTO
respuesta = biseccion(fx,a,b,tolera,vertabla=True)
# SALIDA
print('raíz en: ', respuesta)

# GRAFICA
import matplotlib.pyplot as plt
muestras = 21
 
xi = np.linspace(a,b,muestras)
fi = fx(xi)
plt.plot(xi,fi, label='f(x)')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Biseccion')
plt.grid()
plt.legend()
plt.show()