Ejercicio: 2Eva2012TI_T2 EDO Modelo de clima x,y,z
Se deja de tarea realizar las tres primeras iteraciones en papel.
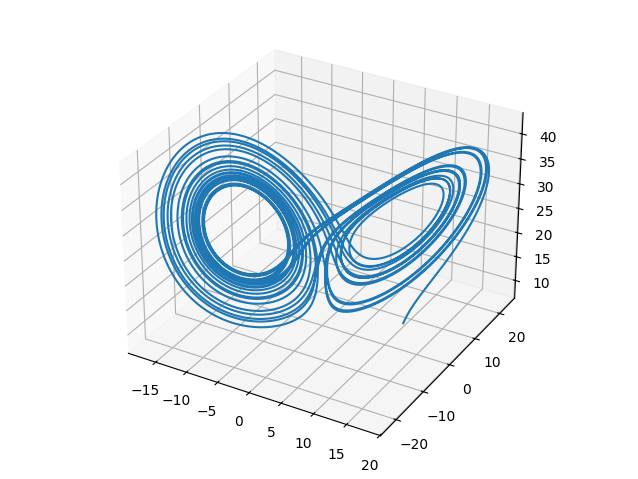
Se presenta el resultado usando el algoritmo de segundo grado como una variante a la respuesta usada como ejemplo.
[ ti, xi, yi, zi]
[[ 0.0000e+00 1.0000e+01 7.0000e+00 7.0000e+00]
[ 2.5000e-03 9.9323e+00 7.5033e+00 7.1335e+00]
[ 5.0000e-03 9.8786e+00 7.9988e+00 7.2774e+00]
...
[ 2.4995e+01 -8.4276e+00 -2.7491e+00 3.3021e+01]
[ 2.4998e+01 -8.2860e+00 -2.6392e+00 3.2858e+01]
[ 2.5000e+01 -8.1453e+00 -2.5346e+00 3.2692e+01]]Algoritmo en Python
# 2Eva_IT2012_T2 Modelo de clima
# MATG1013 Análisis Numérico
import numpy as np
import matplotlib.pyplot as plt
def rungekutta2_fg(f,g,j,t0,x0,y0,z0,h,muestras):
tamano = muestras + 1
estimado = np.zeros(shape=(tamano,4),dtype=float)
# incluye el punto [t0,x0,y0,z0]
estimado[0] = [t0,x0,y0,z0]
ti = t0
xi = x0
yi = y0
zi = z0
for i in range(1,tamano,1):
K1x = h * f(ti,xi,yi,zi)
K1y = h * g(ti,xi,yi,zi)
K1z = h * j(ti,xi,yi,zi)
K2x = h * f(ti+h,xi + K1x, yi + K1y, zi + K1z)
K2y = h * g(ti+h,xi + K1x, yi + K1y, zi + K1z)
K2z = h * j(ti+h,xi + K1x, yi + K1y, zi + K1z)
xi = xi + (K1x+K2x)/2
yi = yi + (K1y+K2y)/2
zi = zi + (K1z+K2z)/2
ti = ti + h
estimado[i] = [ti,xi,yi,zi]
return(estimado)
#INGRESO
to = 0
xo = 10
yo = 7
zo = 7
f = lambda t,x,y,z: 10*(y-x)
g = lambda t,x,y,z: x*(28-z) - y
j = lambda t,x,y,z: -(8/3)*z + (x*y)
h = 0.0025
muestras = 10000
#PROCEDIMIENTO
#Rugen-Kutta 2_orden
tabla = rungekutta2_fg(f,g,j,to,xo,yo,zo,h,muestras)
#SALIDA
np.set_printoptions(precision=4)
print(' [ ti, xi, yi, zi]')
print(tabla)
# Gráfica 3D
fig = plt.figure()
graf3D = fig.add_subplot(111, projection = '3d')
graf3D.plot(tabla[:,1], tabla[:,2], tabla[:,3])
plt.tight_layout()
plt.show()