Ejercicio: 2Eva2023PAOI_T1 Material para medalla de academia
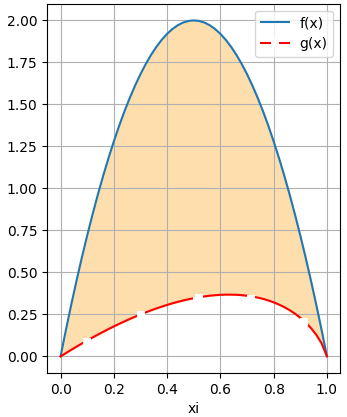
Para f(x) se usará Simpson de 1/3 que requiere al menos dos tramos para aplicar:
a. Realice el planteamiento de las ecuaciones para el ejercicio.
I\cong \frac{h}{3}[f(x_0)+4f(x_1) + f(x_2)]b. Describa el criterio usado para determinar el número de tramos usado en cada caso.
h = \frac{b-a}{2} = \frac{1-0}{2} = 0.5c. Desarrolle las expresiones completas del ejercicio para cada función.
I_{fx}\cong \frac{0.5}{3}[f(0)+4f(0.5) + f(1)] f(0) = 2-8\Big( \frac{1}{2} - (0) \Big)^2 = 0 f(0.5) = 2-8\Big( \frac{1}{2} - (0.5) \Big)^2 = 2 f(1) = 2-8\Big( \frac{1}{2} - (1) \Big)^2 = 0 I_{fx} = \frac{1}{6}[0+4(2) + 0] = \frac{8}{6} = \frac{4}{3} = 1.3333cota de error O(h5) = O(0.55)= O(0.03125)
Para g(x) se usará Simpson de 3/8 que requiere al menos tres tramos para aplicar:
I\cong \frac{3h}{8}[f(x_0)+3f(x_1) +3 f(x_2)+f(x_3)] h = \frac{b-a}{3} = \frac{1-0}{3} = 0.3333 I_{gx}\cong \frac{3(0.3333)}{8}[f(0)+3f(0.3333) +3 f(0.6666)+f(1)] g(0) = -\Big( 1-0\Big)\ln \Big( 1- 0 \Big) = 0 g(0.3333) = -\Big( 1-0.3333\Big)\ln \Big( 1- 0.3333 \Big) = 0.2703 g(0.6666) = -\Big( 1-0.6666\Big)\ln \Big( 1- 0.6666 \Big) = 0.3662 g(0.9999) = -\Big( 1-0.9999\Big)\ln \Big( 1- 0.9999 \Big) = 0para la evaluación numérica de 1 se usa un valor muy cercano desplazado con la tolerancia aplicada.
I_{gx}\cong \frac{3(0.3333)}{8}[0+3(0.2703) + 3(0.3662)+0] = 0.2387d. Indique el resultado obtenido para el área requerida y la cota de error
Area = I_{fx} - I_{gx} = 1.3333 - 0.2387 = 1.0945
cota de error = O(0.03125) + O(0.00411) = 0.03536
e. Encuentre el valor del tamaño de paso si se requiere una cota de error de 0.00032
Si el factor de mayor error es de Simpson 1/3, se considera como primera aproximación que:
cota de error O(h5) = O(0.00032), h = (0.00032)(1/5) = 0.2
es decir el número de tramos es de al menos (b-a)/tramos = 0.2 , tramos = 5.
El número de tramos debe ser par en Simpson de 1/3, por lo que se toma el entero mayor tramos=6 y el tamaño de paso recomendado es al menos 1/6. EL error al aplicar 3 veces la formula es 3(O((1/6)5)) = 0.0003858.
Lo que podría indicar que es necesario al menos dos tramos adicionales con h=1/8 y error O(0,00012) que cumple con el requerimiento.
Se puede aplicar el mismo criterio para Simpson 3/8 y se combinan los errores para verificar que cumplen con el requerimiento.
Algoritmo con Python
Resultados
Ifx: 1.3333332933359998
Igx: 0.238779092876627
Area: 1.094554200459373
Instrucciones en Python usando las funciones
# 2Eva_2023PAOI_T1 Material para medalla de academia
import numpy as np
import matplotlib.pyplot as plt
def integrasimpson13_fi(xi,fi,tolera = 1e-10):
''' sobre muestras de fi para cada xi
integral con método de Simpson 1/3
respuesta es np.nan para tramos desiguales,
no hay suficientes puntos.
'''
n = len(xi)
i = 0
suma = 0
while not(i>=(n-2)):
h = xi[i+1]-xi[i]
dh = abs(h - (xi[i+2]-xi[i+1]))
if dh<tolera:# tramos iguales
unS13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2])
suma = suma + unS13
else: # tramos desiguales
suma = 'tramos desiguales'
i = i + 2
if i<(n-1): # incompleto, faltan tramos por calcular
suma = 'tramos incompletos, faltan '
suma = suma ++str((n-1)-i)+' tramos'
return(suma)
def integrasimpson38_fi(xi,fi,tolera = 1e-10):
''' sobre muestras de fi para cada xi
integral con método de Simpson 3/8
respuesta es np.nan para tramos desiguales,
no hay suficientes puntos.
'''
n = len(xi)
i = 0
suma = 0
while not(i>=(n-3)):
h = xi[i+1]-xi[i]
h1 = (xi[i+2]-xi[i+1])
h2 = (xi[i+3]-xi[i+2])
dh = abs(h-h1)+abs(h-h2)
if dh<tolera:# tramos iguales
unS38 = fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]
unS38 = (3/8)*h*unS38
suma = suma + unS38
else: # tramos desiguales
suma = 'tramos desiguales'
i = i + 3
if (i+1)<n: # incompleto, tramos por calcular
suma = 'tramos incompletos, faltan '
suma = suma +str(n-(i+1))+' tramos'
return(suma)
# INGRESO
fx = lambda x: 2-8*(0.5-x)**2
gx = lambda x: -(1-x)*np.log(1-x)
a = 0
b = 1-1e-4
muestras1 = 2+1
muestras2 = 3+1
# PROCEDIMIENTO
xi1 = np.linspace(a,b,muestras1)
xi2 = np.linspace(a,b,muestras2)
fi = fx(xi1)
gi = gx(xi2)
Ifx = integrasimpson13_fi(xi1,fi)
Igx = integrasimpson38_fi(xi2,gi)
Area = Ifx - Igx
# SALIDA
print('Ifx: ', Ifx)
print('Igx: ', Igx)
print('Area: ', Area)
plt.plot(xi1,fi,'ob',label='f(x)')
plt.plot(xi2,gi,'or', label='g(x)')
plt.grid()
plt.legend()
plt.xlabel('xi')
# curvas suave con mas muestras (no en evaluación)
xi = np.linspace(a,b,51)
fxi = fx(xi)
gxi = gx(xi)
plt.fill_between(xi,fxi,gxi,color='navajowhite')
plt.plot(xi,fxi,color='blue',linestyle='dotted')
plt.plot(xi,gxi,color='red',linestyle='dotted')
plt.show()