2da Evaluación I Término 2017-2018. 28/Agosto/2017. MATG1013

Tema 1. (30 puntos) El movimiento de un sistema acoplado masa-resorte está descrito por la ecuación diferencial ordinaria que sigue:

m\frac{\delta ^2x}{\delta t^2} + c\frac{\delta x}{\delta t} + kx =0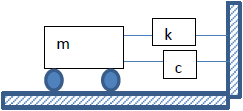

Donde:

x = el desplazamiento desde la posición de equilibrio (m)

t = tiempo (s)

m = 20 kg masa

c = 5 (N s/m) coeficiente de amortiguamiento(sub_amortiguado)

k = 20 (N/m) constante del resorte

La velocidad inicial es cero y el desplazamiento inicial es 1 m.

a) Resuelva esta ecuación con un método numérico para 0≤ t ≤15 s, (solo planteo)

b) Realice 3 iteraciones con h=0.1 s

c) Estime el error acumulado en la tercera iteración.

Rúbrica: Plantear el sistema 5 hasta puntos, Plantear el modelo del método numérico hasta 10 puntos, Realizar 3 iteraciones hasta 10 puntos y estimar el error hasta 5 puntos.