1. Método de Newton-Raphson - Concepto
Referencia: Burden 2.3 p49, Chapra 6.2 p148, Rodríguez 3.3 p52
Se deduce a partir de la interpretación gráfica o por medio del uso de la serie de Taylor de dos términos.
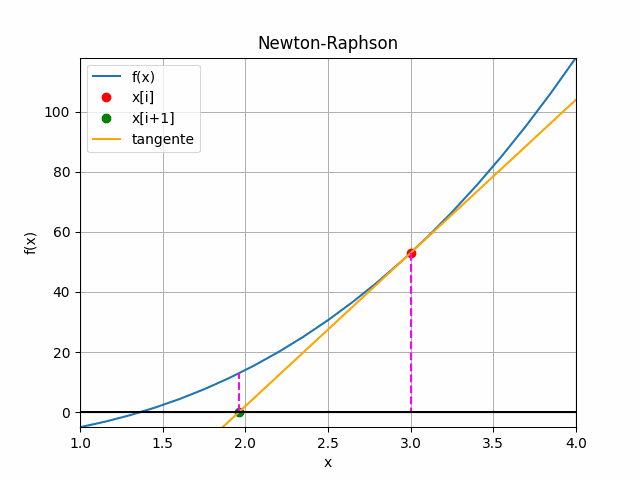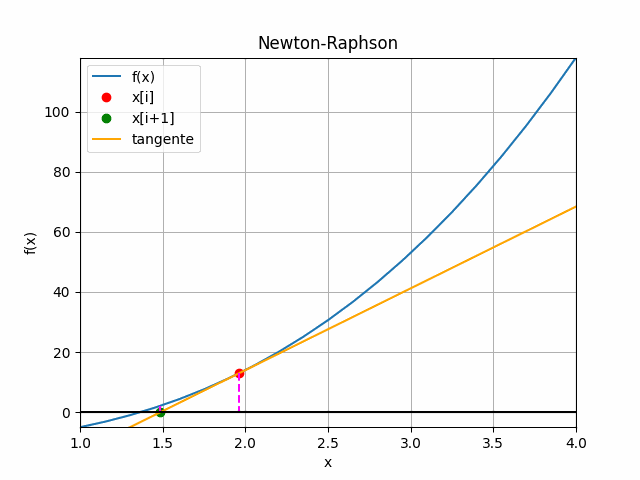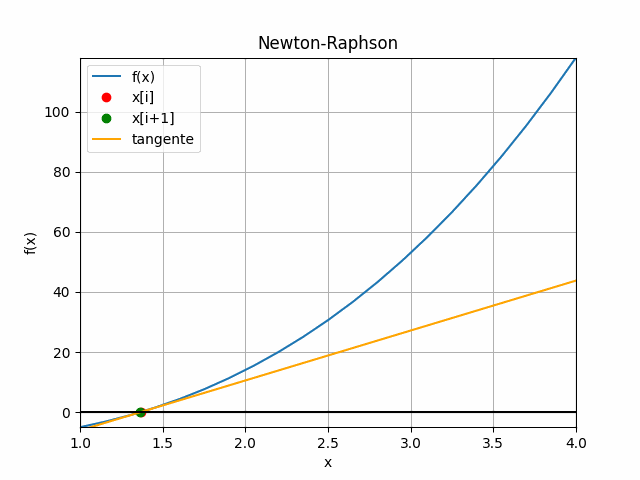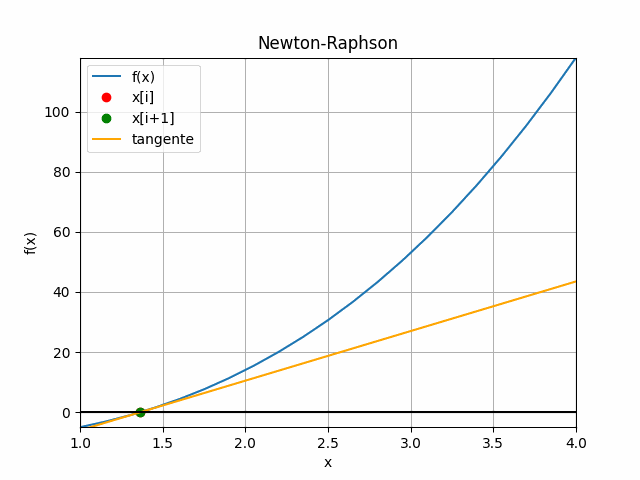
De la gráfica, se usa el triángulo formado por la recta tangente que pasa por f(xi), con pendiente f'(xi) y el eje x.
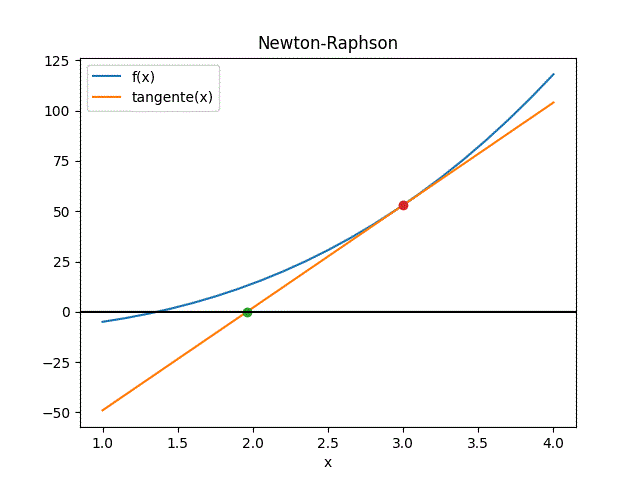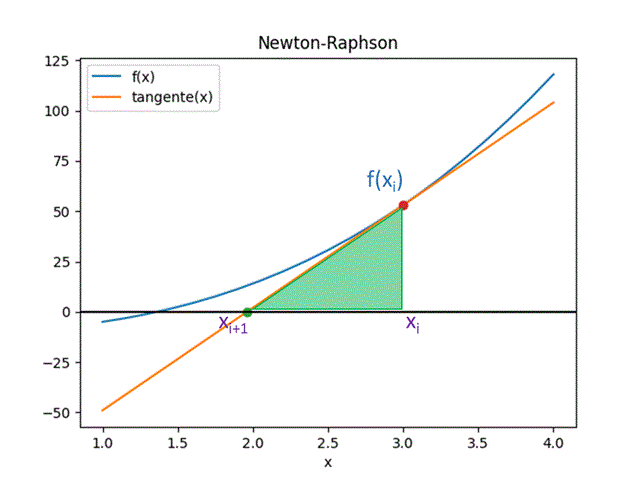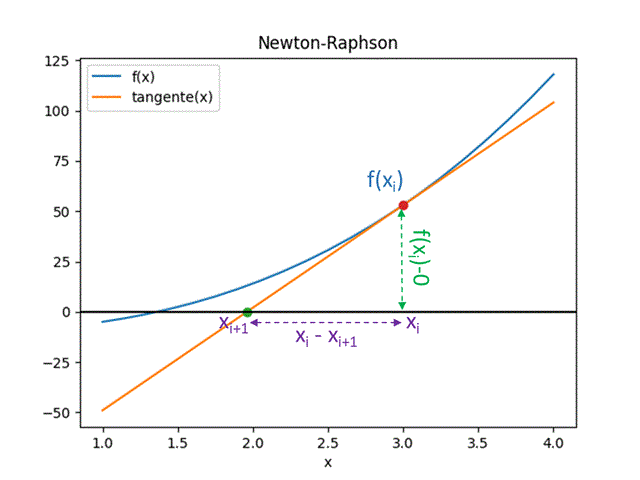
El punto xi+1 es la intersección de la recta tangente con el eje x, que es más cercano a la raíz de f(x), valor que es usado para la próxima iteración.
Reordenando la ecuación de determina la fórmula para el siguiente punto:
x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}El error se determina como la diferencia entre los valores sucesivos encontrados |xi+1 - xi|
La gráfica animada muestra el proceso aplicado varias veces sobre f(x) para encontrar la raíz.
1.1 Recta Tangente para la gráfica
Si se quiere dibujar la recta tangente en el punto inicial, la ecuación de la recta se obtiene usando: el valor de la pendiente con la derivada f'(x) y cambiando la constante b por b0 para no confundirla con la b del intervalo [a,b]
Es necesario disponer de un punto conocido de la recta (x0,f(x0)) y la pendiente en ese punto f'(x0), quedando solo el término de la constante como incógnita .
f(x_0) = f'(x_0) x_0 + b_0 f(x_0) - f'(x_0) x_0 = b_0La función recta tangente se expresa para la gráfica como:
b_0 = f(x_0) - f'(x_0) x_0 rtg(x)= f'(x_0) x + b_0Tarea
Use la serie de Taylor hasta la primera derivada para encontrar el siguiente punto de aproximación xi+1
2. Ejercicio
Referencia: Burden 2.1 ejemplo 1 p38
La ecuación mostrada tiene una raíz en [1,2], ya que f(1)=-5 y f(2)=14.
Muestre los resultados parciales del algoritmo de Newton-Raphson con una tolerancia de 0.0001
f(x) = x^3 + 4x^2 -10 =0
3. Desarrollo Analítico
El método requiere obtener la derivada f'(x) de la ecuación para el factor del denominador.
f(x) = x^3 + 4x^2 -10 f'(x) = 3x^2 + 8x x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}Para el desarrollo se inicia la búsqueda desde un punto en el intervalo [1,2], por ejemplo el extremo derecho, x1=2.
iteración 1
f(2) = (2)^3 + 4(2)^2 -10 = 14 f'(2) = 3(2)^2 + 8(2) = 28 x_{2} = 2 -\frac{14}{28} = 1.5 tramo = |2 -1.5| = 0.5iteración 2
f(1.5) = (1.5)^3 + 4(1.5)^2 -10 = 2.375 f'(1.5) = 3(1.5)^2 + 8(1.5) = 18.75 x_{3} = 1.5 -\frac{2.375}{18.75} = 1.3733 tramo = |1.5 -1.3733| = 0.1267iteración 3
f(1.3733) = (1.3733)^3 + 4(1.3733)^2 -10 = 0.1337 f'(1.3733) = 3(1.3733)^2 + 8(1.3733) = 16.6442 x_{4} = 1.3733 -\frac{0.1337}{16.6442} =1.3652 tramo = |1.3733 -1.3652| = 0.0081La tabla resume los valores de las iteraciones
| iteración | xi | xnuevo | tramo |
|---|---|---|---|
| 1 | 2 | 1.5 | 0.5 |
| 2 | 1.5 | 1.3733 | 0.1267 |
| 3 | 1.3733 | 1.3653 | 0.0081 |
| 4 | ... |
Observe que el error representado por el tramo se va reduciendo entre cada iteración. Se debe repetir las iteraciones hasta que el error sea menor al valor tolerado.
Las demás iteraciones se dejan como tarea
4. Algoritmo con Python
El método de Newton-Raphson se implementa como algoritmo básico en Python
Se muestra el resultado del algoritmo luego de que el tramo alcance un valor menor que tolera.
raiz en: 1.3652300139161466
con error de: 3.200095847999407e-05
A lo expuesto en el video, se añade el control de iteraciones iteramax por si se da el caso que el algoritmo no es convergente.
# Método de Newton-Raphson
import numpy as np
# INGRESO
fx = lambda x: x**3 + 4*(x**2) - 10
dfx = lambda x: 3*(x**2) + 8*x
x0 = 2
tolera = 0.001
iteramax = 100
# PROCEDIMIENTO
itera = 0
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera and itera<iteramax):
fi = fx(xi)
dfi = dfx(xi)
xnuevo = xi - fi/dfi
tramo = abs(xnuevo-xi)
xi = xnuevo
itera = itera + 1
if itera>=iteramax:
xi = np.nan
# SALIDA
print('raiz en: ', xi)
print('con error de: ',tramo)
5. Gráfica en Python
La gráfica presentada para revisar f(x) se realiza con las instrucciones:
# GRAFICA
import matplotlib.pyplot as plt
a = 1
b = 2
muestras = 21
xj = np.linspace(a,b,muestras)
fj = fx(xj)
plt.plot(xj,fj, label='f(x)')
plt.plot(xi,0, 'o')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()
6. Algoritmo en Python como Función
Se convierte el algoritmo a una función, con partes para ver la tabla, y se obtienen los siguientes resultados:
i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo']
0 [ 2. 14. 28. 1.5 0.5]
1 [ 1.5 2.375 18.75 1.3733 0.1267]
2 [1.3733e+00 1.3435e-01 1.6645e+01 1.3653e+00 8.0713e-03]
3 [1.3653e+00 5.2846e-04 1.6514e+01 1.3652e+00 3.2001e-05]
raíz en: 1.3652300139161466
Instrucciones en Python
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)
import numpy as np
import matplotlib.pyplot as plt
def newton_raphson(fx,dfx,xi, tolera, iteramax=100,
vertabla=False, precision=4):
'''fx y dfx en forma numérica lambda
xi es el punto inicial de búsqueda
'''
itera=0
tramo = abs(2*tolera)
if vertabla==True:
print('método de Newton-Raphson')
print('i', ['xi','fi','dfi', 'xnuevo', 'tramo'])
np.set_printoptions(precision)
while (tramo>=tolera):
fi = fx(xi)
dfi = dfx(xi)
xnuevo = xi - fi/dfi
tramo = abs(xnuevo-xi)
if vertabla==True:
print(itera,np.array([xi,fi,dfi,xnuevo,tramo]))
xi = xnuevo
itera = itera + 1
if itera>=iteramax:
xi = np.nan
print('itera: ',itera,
'No converge,se alcanzó el máximo de iteraciones')
return(xi)
# INGRESO
fx = lambda x: x**3 + 4*(x**2) - 10
dfx = lambda x: 3*(x**2) + 8*x
x0 = 2
tolera = 0.001
# PROCEDIMIENTO
respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True)
# SALIDA
print('raíz en: ', respuesta)
La gráfica se la puede añadir usando las instrucciones dadas en el algoritmo básico realizado al inicio par ala comprensión del método.
7. Función en librería scipy.optimize.newton
El método de Newton-Raphson se encuentra implementado en la librería Scipy, que también puede ser usado de la forma:
>>> import scipy as sp
>>> sp.optimize.newton(fx,x0, fprime=dfx, tol = tolera)
1.3652300139161466
>>>
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html
Tarea
Calcule la raíz de f(x) = e-x - x, empleando como valor inicial x0 = 0
- Revisar las modificaciones si se quiere usar la forma simbólica de la función y obtener la derivada con Sympy.