2.3 Método del Punto fijo

Punto fijo

Ejercicio

Analítico

Algoritmo

función

gráfica

librería

1. Método del Punto fijo - Concepto

Referencia: Burden 2.2 p41, Chapra 6.1 p143, Rodríguez 3.2 p44

El método del punto fijo es un método abierto, también llamado de iteración de un punto o sustitución sucesiva, que reordena la ecuación planteada para raíces de ecuaciones

f(x) = 0

separando una x al lado izquierdo de la igualdad.

x = g(x)

Esto permite buscar la intersección entre la recta Identidad y=x y la curva g(x), que es lo que quedó del lado derecho de la igualdad.
Una representación gráfica del proceso de muestra en la gráfica.

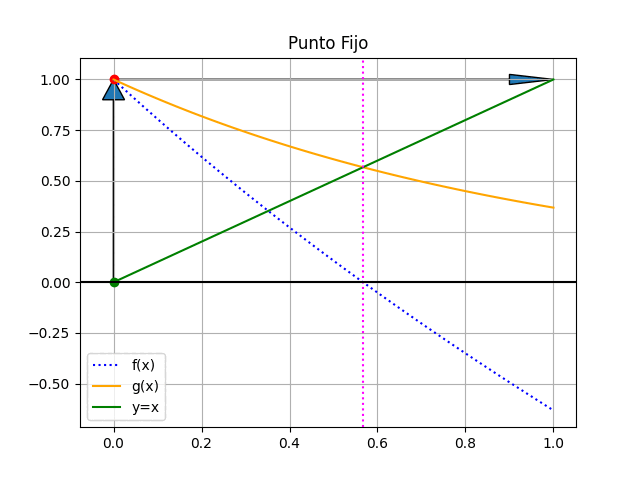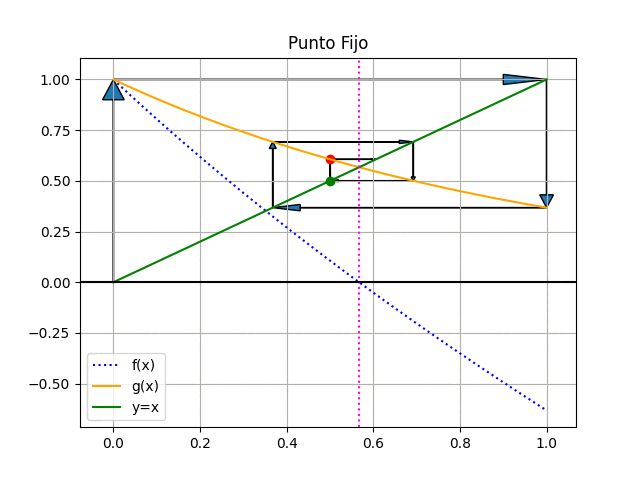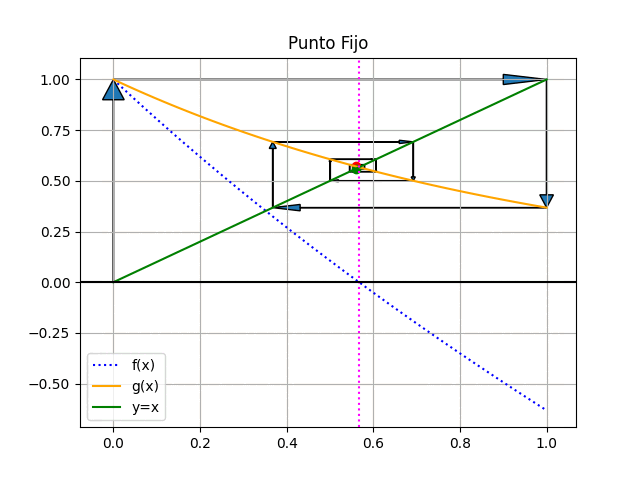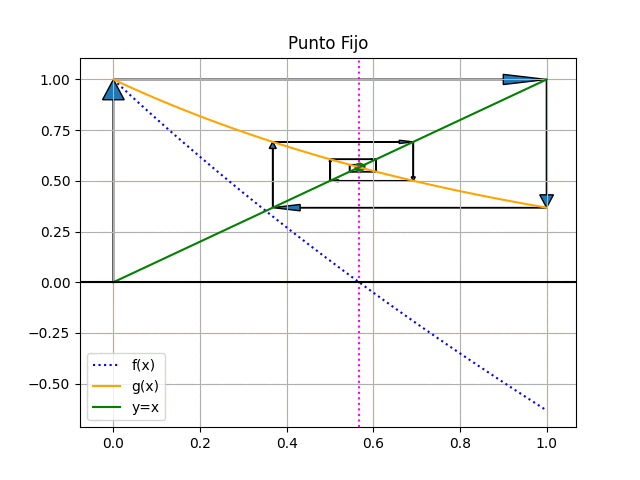
Observe que la raíz de f(x) se encuentra en el mismo valor de x donde ocurre la intersección entre la recta identidad y=x , en color verde, y la función g(x), en color naranja. Como referencia, se usa la linea vertical en x=raíz en color morado.

El método consiste en establecer un punto inicial x₀ para la búsqueda, a partir del cual se calcula el valor g(x₀). En la siguiente iteración el nuevo valor para x es g(x₀), que se refleja en la recta identidad y nuevamente se usa para calcular g(x).

El resultado iterativo se muestra en la figura animada, donde se observa que el resultado es convergente.

1.1 Ejemplos en gráficas

Se muestran algunos ejemplos para destacar lo indicado de forma gráfica.

Ejemplo 1

f(x):e^{-x} - x = 0

se reordena para tener:

x = e^{-x}

g(x) = e^{-x}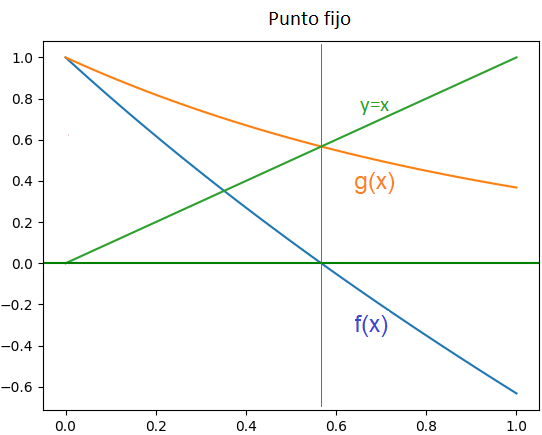

Ejemplo 2

f(x): x^2 - 2x -3 = 0

se reordena para tener:

x = \frac {x^2 - 3}{2}

g(x) = \frac {x^2 - 3}{2}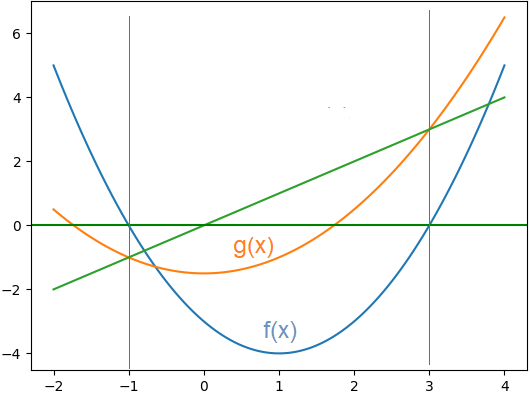

Ejemplo 3

f(x): \sin (x) = 0

puede ser complicado despejar x, por lo que se simplifica el proceso sumando x en ambos lados.

x = \sin (x) + x

g(x) = \sin (x) + x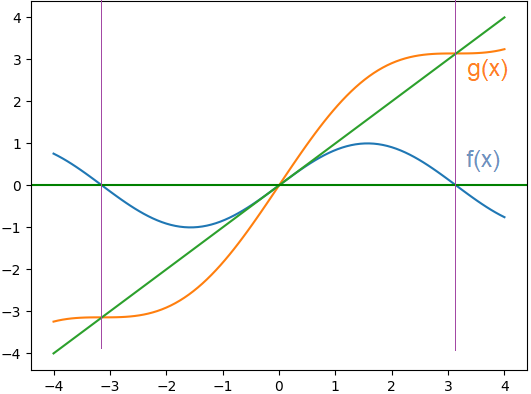

El método proporciona una fórmula para predecir un valor nuevo de x en función del valor anterior:

x_{i+1} = g(x_i)

con error aproximado calculado como:

\epsilon_a = \left| \frac{x_{i+1} - x_i}{x_{i+1}} \right| 100\%

Tarea

Plantee como usar los siguientes conceptos:

¿cuál sería el valor de tolerancia?
¿parámetros de inicio?
compare con con otro método conocido
Revisar el resultado cuando no se cumple que |g'(x)|<1

2. Ejercicio

Referencia: Burden 2.2 p41, Chapra 6.1 p143, Rodríguez 3.2 p44

Encontrar la solución a la ecuación, usando el método del punto fijo, considerando tolerancia de 0.001

f(x): e^{-x} - x = 0

3. Desarrollo Analítico

Al igual que los métodos anteriores, es conveniente determinar el intervalo [a,b] donde es posible evaluar f(x). Se revisa si hay cambio de signo en el intervalo para buscar una raíz. Para el ejemplo, el rango de observación será [0,1], pues f(0)=1 es positivo y f(1)=-0.63 es negativo.

Para el punto fijo, se reordena la ecuación para para tener una ecuación con la variable independiente separada. Se obtiene por un lado la recta identidad y=x, por otro se tiene la función g(x).

f(x): e^{-x} - x = 0

x = e^{-x}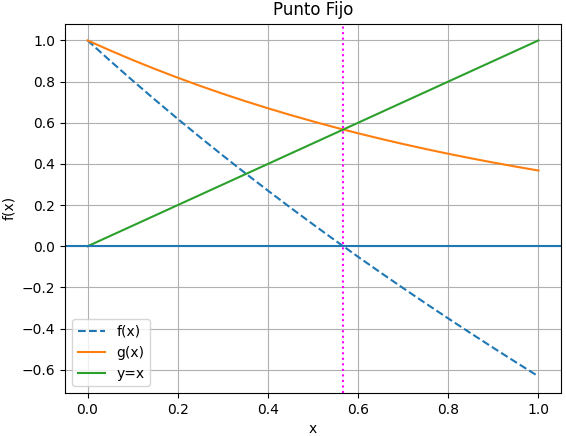

g(x) = e^{-x}

Se buscará la intersección entre las dos expresiones .

Se puede iniciar la búsqueda por uno de los extremos del rango [a,b].

iteración 1

- iniciando desde el extremo izquierdo c=a,

c = 0

- se determina el valor nuevo de gc=g(c) ,

gc = g(0) = e^{-0} = 1

- se determina la diferencia de la aproximación o error = |gc-c|

tramo = |1-0| = 1

- se proyecta en la recta identidad, como el nuevo punto de evaluación

c = gc

- se repite el proceso para el nuevo valor de c, hasta que el error sea menor al tolerado. En caso que el proceso no converge, se utiliza un contador de iteraciones máximo, para evitar tener un lazo infinito.

iteración 2

c = 1

gc = g(1) = e^{-1} = 0.3678

tramo =|0.3678 - 1|= 0.6322

iteración 3

c = 0.3678

gc = e^{-0.3678} = 0.6922

tramo =|0.6922-0.3678|= 0.3244

La tabla resume los valores de las iteraciones

iteración	c	gc= g(c)	\|tramo\|
1	0	1.0	1
2	1.0	*0.3678*	0.6322
3	*0.3678*	0.6922	0.3244
4	0.6922	...
5

El proceso realizado en la tabla se muestra en la gráfica, para una función que converge.

Ejemplo: Método Punto fijo No converge

Cuando la 'x' a separar en la expresión f(x) es otra, el resultado no siempre será convergente. Si para el ejercicio anterior se hubiese despejado la 'x' en el exponencial, la expresión g(x) se obtiene como:

f(x): e^{-x} - x = 0

e^{-x} = x

\ln\Big(e^{-x}\Big) = \ln(x)

-x= \ln(x)

x= -\ln(x)

Al revisar la gráfica del algoritmo se observa que también se cumple que la raíz de f(x) coincide en el valor x con la intersección entre la identidad y g(x).

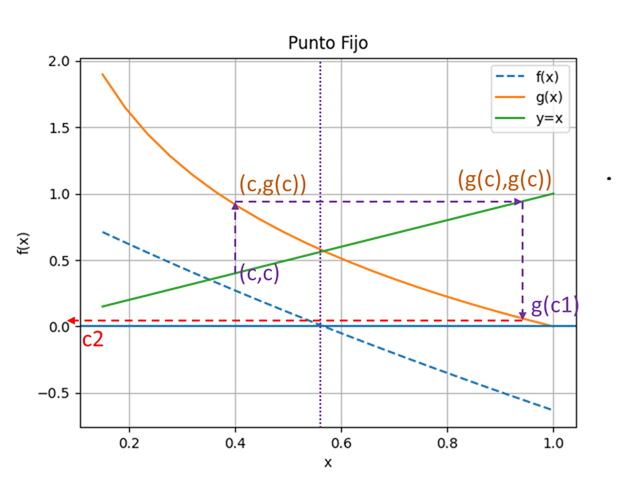
Sin embargo al realizar las iteraciones se tiene que:

iteración 1

c = 0.5
gc = -ln(0.5) = 0.6931
tramo = | 0.6931-0.5| =0.1931

iteración 2

c = 0.6931
gc = -ln(0.6931) = 0.3665
tramo = | 0.3665-0.6931| = 0.3266

iteración 3

c = 0.3665
gc = -ln(0.3665) = 1.0037
tramo = | 1.0037-0.3665| = 0.6372

Se observa que el tramo o error aumenta en cada iteración, con lo que se concluye que de esta forma, la aplicación del método no es convergente.

4. Algoritmo en Python

El algoritmo en Python del video se adjunta para seguimiento. Se requiere la función gx, el punto inicial y la tolerancia, la variable de número de iteraciones máxima, iteramax, permite controlar la convergencia de la función con el método.

El resultado del algoritmo se presenta como:

raíz en:  0.5669089119214953
errado :  0.0006477254067881466
itera  :  14

Instrucciones en Python

# Algoritmo de punto fijo
# error = tolera
import numpy as np

# INGRESO
fx = lambda x: np.exp(-x) - x
gx = lambda x: np.exp(-x)

c = 0  # valor inicial
tolera = 0.001
iteramax = 40

# PROCEDIMIENTO
tramo = 2*tolera # al menos una iteracion
i = 0  # iteración inicial
while tramo>=tolera and i<iteramax:
    gc = gx(c)
    tramo = abs(gc-c)
    c = gc
    i = i + 1

if (i>=iteramax): # Valida convergencia
    c = np.nan

# SALIDA
print('raíz en: ', c)
print('errado : ', tramo)
print('itera  : ', i)

Para obtener la gráfica básica se determinan los puntos para cada función fx y gx. Como los valores de c y gc cambiaron durante el algoritmo, para la siguiente sección es necesario volver a escribirlos u obtener una copia de los valores en otra variable para reutilizarlos en ésta sección.

5. Gráfica en Python

Se añaden las siguiente instrucciones al algoritmo anterior:

# GRAFICA
import matplotlib.pyplot as plt

a = 0  # intervalo de gráfica en [a,b]
b = 1
muestras = 21

# calcula los puntos para fx y gx
xi = np.linspace(a,b,muestras)
fi = fx(xi)
gi = gx(xi)
yi = xi

plt.plot(xi,fi, label='f(x)',
         linestyle='dashed')
plt.plot(xi,gi, label='g(x)')
plt.plot(xi,yi, label='y=x')

plt.axvline(c, color='magenta',
            linestyle='dotted')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Punto Fijo')
plt.grid()
plt.legend()
plt.show()

6. Algoritmo en Python como Función

El resultado del algoritmo como una función y mostrando la tabla de resultados por iteraciones es:

método del Punto Fijo
i ['xi', 'gi', 'tramo']
0 [0. 1. 1.]
1 [1.       0.367879 0.632121]
2 [0.367879 0.692201 0.324321]
3 [0.692201 0.500474 0.191727]
4 [0.500474 0.606244 0.10577 ]
5 [0.606244 0.545396 0.060848]
6 [0.545396 0.579612 0.034217]
7 [0.579612 0.560115 0.019497]
8 [0.560115 0.571143 0.011028]
9 [0.571143 0.564879 0.006264]
10 [0.564879 0.568429 0.003549]
11 [0.568429 0.566415 0.002014]
12 [0.566415 0.567557 0.001142]
13 [0.567557 0.566909 0.000648]
raíz en:  0.5669089119214953

Instrucciones en Python

# Algoritmo de punto fijo
# error = tolera
import numpy as np

def puntofijo(gx,c,tolera,iteramax=40,vertabla=True, precision=6):
    """
    g(x) se obtiene al despejar una x de f(x)
    máximo de iteraciones predeterminado: iteramax
    si no converge hasta iteramax iteraciones
    la respuesta es NaN (Not a Number)
    """
    itera = 0 # iteración inicial
    tramo = 2*tolera # al menos una iteracion
    if vertabla==True:
        print('método del Punto Fijo')
        print('i', ['xi','gi','tramo'])
        np.set_printoptions(precision)
    while (tramo>=tolera and itera<=iteramax):
        gc = gx(c)
        tramo = abs(gc-c)
        if vertabla==True:
            print(itera,np.array([c,gc,tramo]))
        c = gc
        itera = itera + 1
    respuesta = c
    # Valida respuesta
    if itera>=iteramax:
        respuesta = np.nan
        print('itera: ',itera,
              'No converge,se alcanzó el máximo de iteraciones')
    return(respuesta)

# PROGRAMA ----------------------
# INGRESO
fx = lambda x: np.exp(-x) - x
gx = lambda x: np.exp(-x)

c = 0  # valor inicial
tolera = 0.001
iteramax = 15

# PROCEDIMIENTO
respuesta = puntofijo(gx,c,tolera,iteramax,vertabla=True)

# SALIDA
print('raíz en: ', respuesta)

De añadirse la parte gráfica, el bloque requiere el intervalo de observación [a,b].

7. Función en librería Scipy.optimize.fixed_point

El método del punto fijo se encuentra implementado en Scipy, que también puede ser usado de la forma:

>>> import numpy as np
>>> import scipy as sp
>>> gx = lambda x: np.exp(-x)
>>> c = 0
>>> sp.optimize.fixed_point(gx,c,xtol=0.001,maxiter=15)
array(0.5671432948307147)

el valor predeterminado de iteraciones si no se escribe es 500 y la tolerancia predeterminada es xtol=1e-08
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fixed_point.html

Tarea

Revisar lo que sucede cuando el valor inicial a esta a la derecha de la raíz.
Validar que la función converge, revisando que |g'(x)|<1, o que la función g(x) tenga pendiente menor a pendiente de la recta identidad.