1. Método de Gauss
Referencia: Chapra 9.2 p254, Burden 6.1 p273, Rodríguez 4.3 p119
El método de Gauss opera sobre la matriz aumentada y pivoteada por filas, añadiendo los procesos:
\begin{cases} a_{0,0} x_0+a_{0,1}x_1+a_{0,2} x_2 = b_{0} \\ a_{1,0} x_0+a_{1,1}x_1+a_{1,2} x_2 = b_{1} \\ a_{2,0} x_0+a_{2,1}x_1+a_{2,2} x_2 = b_{2} \end{cases}1.1 Eliminación hacia adelante

Desde la primera fila i ,
sobre las filas inferiores
k = i+1, i+2, ...
a_{k} = a_{k} -a_{i}\frac{a_{ki}}{a_{ii}}1.2 Sustitución hacia atrás
Desde la última fila, para
i = n-1, n-2, ...
x_i = \Bigg( b_i-\sum_{j=i+1}^{n} a_{ij} x_{j} \Bigg) \frac{1}{a_{ii}}y las columnas j luego de la diagonal.
2. Ejercicio

Referencia: Rodríguez 4.0 p105, 1Eva2010TI_T3_MN Precio artículos
Para el sistema de ecuaciones mostrado, desarrolle usando el método de Gauss.
\begin{cases} 4x_1+2x_2+5x_3 = 60.70 \\ 2x_1+5x_2+8x_3 = 92.90 \\ 5x_1+4x_2+3x_3 = 56.30 \end{cases}Se aplica el pivoteo parcial por filas,

que tiene como resultado:
\left( \begin{array}{rrr|r} 5 & 4 & 3 & 56.3 \\ 2 & 5 & 8 & 92.9 \\ 4 & 2 & 5 & 60.7 \end{array} \right)
[[ 5. 4. 3. 56.3]
[ 2. 5. 8. 92.9]
[ 4. 2. 5. 60.7]]
3. Eliminación hacia adelante o eliminación Gaussiana
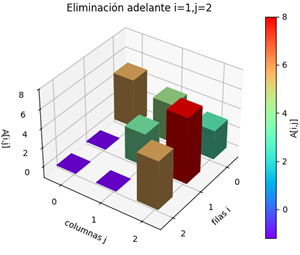
Consiste en simplificar la matriz a una triangular superior, con ceros debajo de la diagonal, usando operaciones entre filas, para obtener:
\left( \begin{array}{rrr|r} 5 & 4 & 3 & 56.3 \\ 0 & 3.4 & 6.8 & 70.38 \\ 0 & 0 & 5 & 40.5 \end{array} \right)Elimina hacia adelante
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]Los índices de fila y columna en la matriz A[i,j] se usan de forma semejante a la nomenclatura de los textos de Álgebra Lineal.
Progresivamente para cada fila, se toma como referencia o pivote el elemento de la diagonal (i=j).
Luego, se realizan operaciones con las filas inferiores para convertir los elementos por debajo de la diagonal en cero.
Las operaciones ya incluyen el vector B debido a que se trabaja sobre la matriz aumentada AB.
AB Matriz aumentada y pivoteada por filas:
[[ 5. 4. 3. 56.3]
[ 2. 5. 8. 92.9]
[ 4. 2. 5. 60.7]]iteración fila 1, operación fila 1 y 2
Para la fila 1, con posición i=0, se usa el elemento ai,i como pivote.
pivote = AB[i,i] = AB[0,0] = 5Para las filas que están después de la diagonal se referencian como k. Se obtiene el factor escalar de la operación entre filas de la fórmula.
k = i+1 = 0+1 = 1
factor = AB[1,0]/pivote = 2/5
y se realiza la operación entre fila k y la fila i para actualizar la fila k,
[ 2. 5. 8. 92.9]
-(2/5)*[ 5. 4. 3. 56.3]
__________________________
= [ 0. 3.4 6.8 70.38]con lo que la matriz aumentada AB se actualiza a:
AB =
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 4. 2. 5. 60.7 ]]
iteración fila 1, operación fila 1 y 3
Se continúa con la siguiente fila, quedando la matriz aumentada con la columna debajo de la primera diagonal en cero:
k = k+1 = 2
factor = 4/5 [ 4. 2. 5. 60.7]
- (4/5)*[ 5. 4. 3. 56.3]
_____________________________
= [ 0. -1.2 2.6 15.66]
AB =
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. -1.2 2.6 15.66]]Como ya se terminaron las operaciones con la primera posición de la diagonal, el siguiente paso es usar la segunda posición, i =1.
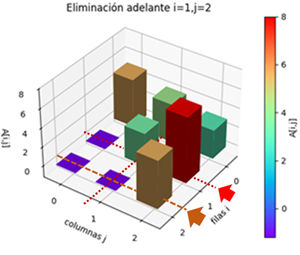
iteración fila 2
Para la fila 2, con posición i=1, se toma el elemento de la diagonal ai,i como pivote, la variable adelante indica la referencia de la tercera fila
pivote = A[i,i] = AB[1,1] = 3.4Para las filas ubicadas adelante de la diagonal se referencian como k. Para aplicar la fórmula por filas, se obtiene el factor .
k = i+1 = 1+1 = 2
factor = AB[2,1]/pivote = -1.2/3.4 = - 0,3529
[ 0. -1.2 2.6 15.66]
-(-1.2/3.4)*[ 0. 3.4 6.8 70.38]
________________________________
= [ 0. 0. 5. 40.5 ]
AB =
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]
Con lo que se completa el objetivo de tener ceros debajo de la diagonal.
Observe que no es necesario realizar operaciones para la última fila, por lo que k debe llegar solamente hasta la fila penúltima.
El resultado de la eliminación hacia adelante, a ser usado en el próximo paso es:
\left( \begin{array}{rrr|r} 5 & 4 & 3 & 56.3 \\ 0 & 3.4 & 6.8 & 70.38 \\ 0 & 0 & 5 & 40.5 \end{array} \right)4. Sustitución hacia atrás
La fórmula se interpreta para facilitar el algoritmo.
Desde la última fila, para i = n-1, n-2, ...
Y las columnas j luego de la diagonal
x_i = \Bigg( b_i-\sum_{j=i+1}^{n} a_{ij} x_{j} \Bigg) \frac{1}{a_{ii}}Para una fila i, el vector B[i] representa el valor de la constante en la fila i de la matriz aumentada, A[i,j] se refiere los valores de los coeficientes de la ecuación, de los que se encuentran a la derecha de la diagonal.
Las operaciones se realizan de abajo hacia arriba desde la última fila. Para el ejercicio presentado se tiene que:
ultfila = n-1 = 3-1 = 2
ultcolumna = m-1 = 4-1 = 3
la matriz a procesar es la resultante de eliminación hacia adelante:
\left( \begin{array}{rrr|r} 5 & 4 & 3 & 56.3 \\ 0 & 3.4 & 6.8 & 70.38 \\ 0 & 0 & 5 & 40.5 \end{array} \right)Elimina hacia adelante
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]iteración 1, fila 3, i=2
Empieza desde la última fila de la matriz,
[ 0. 0. 5. 40.5 ]El valor de la constante es B[i] = 40.5 y no existen elementos hacia la derecha de la diagonal. No se usa la ultima columna que es de las constantes:
5 x_3 = 40.5 x_3 = \frac{40.5}{5} = 8.1la respuesta se interpreta en el vector X como:
X= [ x_1 , x_2 , x_3] = [ 0 , 0 , 8.1 ]iteración 2, fila 2, i = 1
De la penúltima fila se obtiene la ecuación para encontrar x2
[ 0. 3.4 6.8 70.38]se observa que B[i] = 70.38 y a la derecha de a diagonal se tiene un solo valor de 6.8.
3.4 x_2 = 70.38 -6.8 x_3 3.4 x_2 = 70.38 -6.8 (8.1)Usa el valor de x3 encontrado en la iteración anterior. Muestra la ecuación para la segunda fila.
x_2 = \frac{70.38 -6.8 (8.1)}{3.4} = 4.5la respuesta se interpreta en el vector X como:
X= [ 0 , 4.5 , 8.1 ]iteración 3 fila 1, i=0
Se sigue el mismo proceso para la siguiente incógnita x1 que se interpreta como
[ 5. 4. 3. 56.3 ]Se encuentra que la solución al sistema de ecuaciones es:
X= [ 2.8, 4.5 , 8.1 ]
Método de Gauss
solución X:
[2.8 4.5 8.1]
Verificar respuesta
Para verificar que el resultado es correcto, se usa el producto punto entre la matriz a y el vector resultado X. La operación A.X = B debe dar el vector B.
>>> A
array([[4., 2., 5.],
[2., 5., 8.],
[5., 4., 3.]])
>>> X
array([2.8, 4.5, 8.1])
>>> np.dot(A,X)
array([60.7, 92.9, 56.3])
5. Algoritmo con Python
El algoritmo para el Método de Gauss, reutiliza las instrucciones para matriz aumentada y pivoteo parcial por filas.
Recordar: Asegurar que los arreglos sean de tipo número Real (float), para que no se considere el vector como entero y realice operaciones entre enteros, generando errores por truncamiento.
El resultado del algoritmo muestra los siguientes resultados:
Pivoteo parcial por filas AB: ----
[[ 5. 4. 3. 56.3]
[ 2. 5. 8. 92.9]
[ 4. 2. 5. 60.7]]
Eliminación hacia adelante: ------
i: 0 k: 1 factor: 0.4
i: 0 k: 2 factor: 0.8
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. -1.2 2.6 15.66]]
i: 1 k: 2 factor: -0.3529411764705883
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]
Método de Gauss
solución X:
[2.8 4.5 8.1]
La parte nueva a desarrollar corresponde al procedimiento de "eliminación hacia adelante" y el procedimiento de "sustitución hacia atrás".
# Método de Gauss
# Sistemas de Ecuaciones A.X=B
import numpy as np
# INGRESO
# NOTA: Para AB, se ha usado pivoteo parcial por filas
A = [[4,2,5],
[2,5,8],
[5,4,3]]
B = [60.70, 92.90, 56.30]
# PROCEDIMIENTO
# Matrices como arreglo, numeros reales
A = np.array(A,dtype=float)
B = np.array(B,dtype=float)
# Matriz aumentada AB
B_columna = np.transpose([B])
AB = np.concatenate((A,B_columna),axis=1)
# Pivoteo parcial por filas
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
# Para cada fila en AB
for i in range(0,n-1,1):
# columna desde diagonal i en adelante
columna = abs(AB[i:,i])
dondemax = np.argmax(columna)
if (dondemax !=0): # NO en diagonal
# intercambia filas
temporal = np.copy(AB[i,:])
AB[i,:] = AB[dondemax+i,:]
AB[dondemax+i,:] = temporal
print('Pivoteo parcial por filas AB: ----')
print(AB)
# Eliminación hacia adelante
print('Eliminación hacia adelante: ------')
for i in range(0,n-1,1): # una fila
pivote = AB[i,i]
adelante = i + 1
for k in range(adelante,n,1): # diagonal adelante
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - AB[i,:]*factor
print('i:',i,'k:',k, 'factor:',factor)
print(AB)
# Sustitución hacia atrás
ultfila = n-1
ultcolumna = m-1
X = np.zeros(n,dtype=float)
for i in range(ultfila,0-1,-1):
suma = AB[i,ultcolumna]
for j in range(i+1,ultcolumna,1):
suma = suma - AB[i,j]*X[j]
X[i] = suma/AB[i,i]
# SALIDA
print('Método de Gauss')
print('solución X: ')
print(X)
Tarea
Revisar cuando la matriz pivoteada por filas tienen en la diagonal un elemento cero o muy cercano a 0, la matriz sería singular. El valor considerado como casi cero podría ser 1x10-15
A estas alturas, por la cantidad de líneas de instrucción es recomendable reutilizar bloques de algoritmos usando funciones def-return. Por ejemplo: pivoteo por filas, eliminación hacia adelante, sustitución hacia atrás.
6. Algoritmo como función de Python
Se integra la función pivoteafila(), se crean las funciones para los procedimientos gauss_eliminaAdelante() y gauss_sustituyeAtras(), usando la variable vertabla para observar los resultados parciales.
# Método de Gauss
# Sistemas de Ecuaciones A.X=B
import numpy as np
def gauss_eliminaAdelante(AB,vertabla=False,casicero = 1e-15):
''' Gauss elimina hacia adelante
tarea: verificar términos cero
'''
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
if vertabla==True:
print('Elimina hacia adelante:')
for i in range(0,n,1):
pivote = AB[i,i]
adelante = i+1
if vertabla==True:
print(' fila i:',i,' pivote:', pivote)
for k in range(adelante,n,1):
if (np.abs(pivote)>=casicero):
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - factor*AB[i,:]
for j in range(0,m,1): # casicero revisa
if abs(AB[k,j])<casicero:
AB[k,j]=0
if vertabla==True:
print(' fila k:',k,
' factor:',factor)
else:
print(' pivote:', pivote,'en fila:',i,
'genera division para cero')
if vertabla==True:
print(AB)
return(AB)
def gauss_sustituyeAtras(AB,vertabla=False,casicero = 1e-15):
''' Gauss sustituye hacia atras
'''
n,m = np.shape(AB)
# Sustitución hacia atras
if vertabla==True:
print('Sustitute hacia atras:')
X = np.zeros(n,dtype=float)
ultfila = n-1
ultcolumna = m-1
for i in range(ultfila,0-1,-1):
suma = AB[i,ultcolumna] # B[i]
for j in range(i+1,ultcolumna,1):
suma = suma - AB[i,j]*X[j]
X[i] = suma/AB[i,i] # suma/pivote
if vertabla==True:
print(' fila i:',i,
' X['+str(i)+']:',X[i])
return(X)
def pivoteafila(A,B,vertabla=False):
'''
Pivoteo parcial por filas, entrega matriz aumentada AB
Si hay ceros en diagonal es matriz singular,
Tarea: Revisar si diagonal tiene ceros
'''
A = np.array(A,dtype=float)
B = np.array(B,dtype=float)
# Matriz aumentada
nB = len(np.shape(B))
if nB == 1:
B = np.transpose([B])
AB = np.concatenate((A,B),axis=1)
if vertabla==True:
print('Matriz aumentada')
print(AB)
print('Pivoteo parcial:')
# Pivoteo por filas AB
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
# Para cada fila en AB
pivoteado = 0
for i in range(0,n-1,1):
# columna desde diagonal i en adelante
columna = np.abs(AB[i:,i])
dondemax = np.argmax(columna)
# dondemax no es en diagonal
if (dondemax != 0):
# intercambia filas
temporal = np.copy(AB[i,:])
AB[i,:] = AB[dondemax+i,:]
AB[dondemax+i,:] = temporal
pivoteado = pivoteado + 1
if vertabla==True:
print(' ',pivoteado,
'intercambiar filas: ',i,
'con', dondemax+i)
if vertabla==True:
if pivoteado==0:
print(' Pivoteo por filas NO requerido')
else:
print('AB:')
print(AB)
return(AB)
# PROGRAMA Búsqueda de solucion --------
# INGRESO
A = [[4,2,5],
[2,5,8],
[5,4,3]]
B = [60.70,92.90,56.30]
# PROCEDIMIENTO
AB = pivoteafila(A,B,vertabla=True)
AB = gauss_eliminaAdelante(AB,vertabla=True)
X = gauss_sustituyeAtras(AB,vertabla=True)
# SALIDA
print('Método de Gauss')
print('solución X: ')
print(X)
El resultado para el ejercicio anterior es:
Matriz aumentada
[[ 4. 2. 5. 60.7]
[ 2. 5. 8. 92.9]
[ 5. 4. 3. 56.3]]
Pivoteo parcial:
1 intercambiar filas: 0 con 2
[[ 5. 4. 3. 56.3]
[ 2. 5. 8. 92.9]
[ 4. 2. 5. 60.7]]
Elimina hacia adelante:
fila i: 0 pivote: 5.0
fila k: 1 factor: 0.4
fila k: 2 factor: 0.8
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. -1.2 2.6 15.66]]
fila i: 1 pivote: 3.4
fila k: 2 factor: -0.3529411764705883
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]
fila i: 2 pivote: 5.0
[[ 5. 4. 3. 56.3 ]
[ 0. 3.4 6.8 70.38]
[ 0. 0. 5. 40.5 ]]
Sustitute hacia atras:
fila i: 2 X[2]: 8.100000000000003
fila i: 1 X[1]: 4.499999999999997
fila i: 0 X[0]: 2.8
Método de Gauss
solución X:
[2.8 4.5 8.1]