4.2.2 Interpolación por Diferencias divididas de Newton (Δx) con Python

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..

1. Diferencias divididas de Newton

Referencia: Chapra 18.1.3 p508, Rodríguez 6.7 p223, Burden 9Ed 3.3 p124.

El método se usa en el caso que los puntos en el "eje x" se encuentran espaciados de forma arbitraria y provienen de una función desconocida pero supuestamente diferenciable.

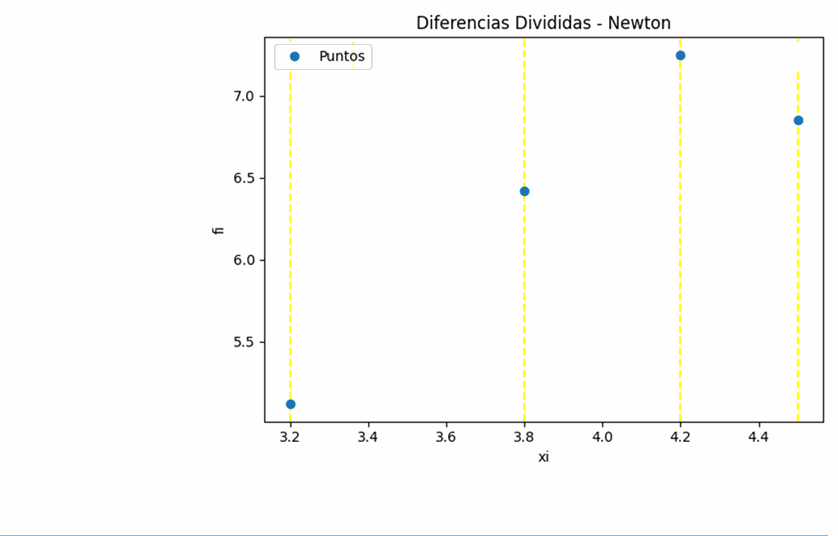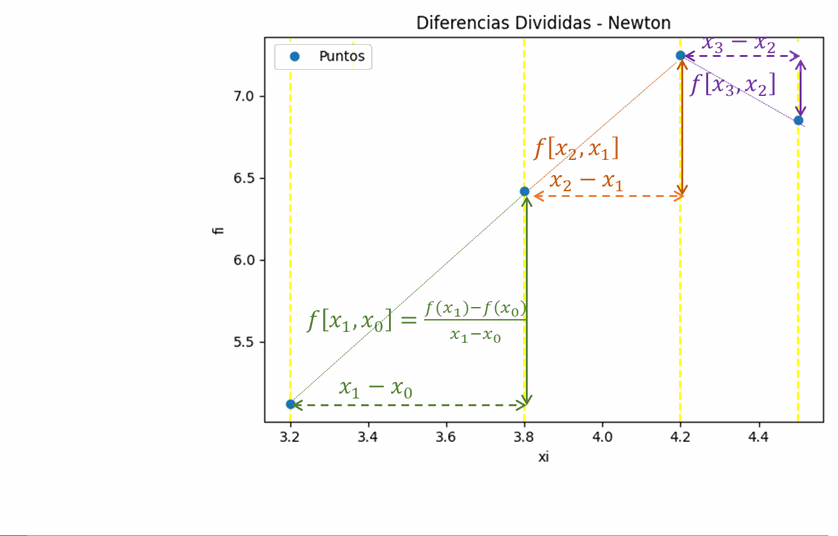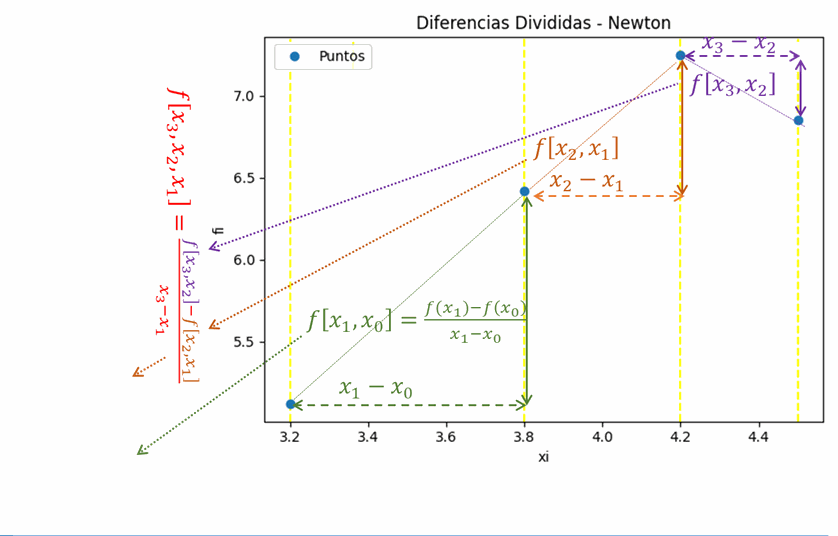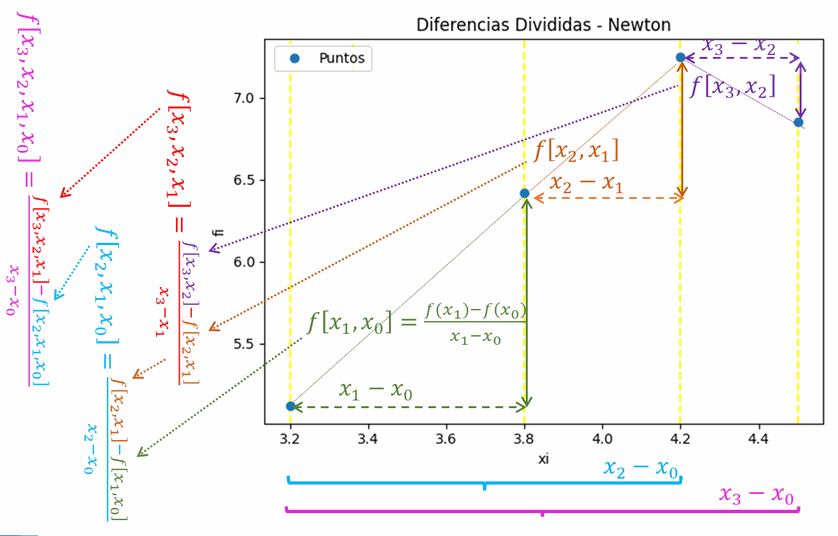
La n-ésima diferencia dividida finita es:

f[x_{n}, x_{n-1}, \text{...}, x_{1}, x_{0}] = \frac{f[x_{n}, x_{n-1}, \text{...}, x_{1}]- f[x_{n-1}, x_{n-2}, \text{...}, x_{0}]}{x_{n}-x_{0}}

Para lo cual se debe interpretar la tabla de diferencias divididas, también como una aproximación a una derivada:

i	x_i	f[x_i]	Primero	Segundo	Tercero
0	x₀	f[x₀]	f[x₁,x₀]	f[x₂,x₁,x₀]	f[x₃,x₂,x₁,x₀]
1	x₁	f[x₁]	f[x₂,x₁]	f[x₃,x₂,x₁]
2	x₂	f[x₂]	f[x₃,x₂]
3	x₂	f[x₃]

En la fórmula del polinomio, las diferencias divididas sirven para evaluar los coeficientes de cada término adicional para aumentar el grado. Semejante al proceso realizado para "diferencias finitas divididas":

f_n(x) = f(x_0)+(x-x_0)f[x_1,x_0] +

+ (x-x_0)(x-x_1)f[x_2,x_1,x_0] + \text{...}+

+ (x-x_0)(x-x_1)\text{...}(x-x_{n-1})f[x_n,x_{n-1},\text{...},x_0]

Este polinomio de interpolación se conoce como de Newton en diferencias divididas.

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..

2. Ejercicio

Referencia: 1Eva_IIT2008_T3_MN Ganancia en inversión

Se dispone de los datos (x, f(x)), en donde x es un valor de inversión y f(x) es un valor de ganancia, ambos en miles de dólares:

inversión	ganancia
3.2	5.12
3.8	6.42
4.2	7.25
4.5	6.85

Considere que los valores invertidos en materia prima para producción, dependen de la demanda de del producto en el mercado, motivo por el que los valores de inversión no guardan distancias equidistantes entre si.

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]

3. Desarrollo analítico

Se toman los datos de la tabla como arreglos para el algoritmo

xi = [3.2 , 3.8 , 4.2 , 4.5 ]
fi = [5.12, 6.42, 7.25, 6.85]

Con los datos se llena la tabla de diferencias divididas, donde por simplicidad, se escriben las operaciones en cada casilla. La última columna o cuarta diferencia dividida es cero por no disponer de datos para hacer el cálculo.

i	x_i	f[x_i]	Primero	Segundo	Tercero
0	3.2	5.12	$\frac{6.42-5.12}{3.8-3.2} =2.1667$	$\frac{2.075-2.1667}{4.2-3.2} =-0.0917$	$\frac{-4.869-(-0.0917)}{4.5-3.2} =-3.6749$
1	3.8	6.42	$\frac{7.25-6.42}{4.2-3.8} =2.075$	$\frac{-1.3333-2.075}{4.5-3.8} =-4.869$
2	4.2	7.25	$\frac{6.85-7.25}{4.5-4.2} =-1.3333$
3	4.5	6.85

Las diferencias divididas de la primera fila son los valores usados para la expresión del polinomio de interpolación:

ddividida = tabla[0,3:] 
          = [ 2.1667, -0.0917, -3.6749, 0. ]

La expresión del polinomio inicia con el primer valor de la función f(x0).

p_3(x) = f_0 = 5.12

se calcula el primer término usando el factor de la primera diferencia dividida y se añade a la expresión del polinomio.

término = (x-x_0)f[x1,x0] = (x-3.2)2.1667

p_3(x) = 5.12 + 2.1667(x-3.2)

con el siguiente valor de ddividida[] se procede de manera semejante:

término = (x-x_0)(x-x_1)f[x1,x0] =

= (x-3.2)(x-3.8)(-0.0917)

p_3(x) = 5.12 + 2.1667(x-3.2)+

+ (-0.0917)(x-3.2)(x-3.8)

Realizando el cálculo del tercer y último termino con diferencias divididas, el polinomio obtenido es:

p_3(x) = 5.12 + 2.1667(x-3.2) +

+ (-0.0917)(x-3.2)(x-3.8) +

+ (-3.6749)(x - 3.2)(x - 3.8)(x - 4.2)

que simplificando al multiplicar entre los términos (x-xi):

p_3(x) = 184.7569 - 149.9208 x + 41.0673 x^2 - 3.6749 x^3

El polinomio en el intervalo de xi, en la gráfica muestra que pasa por todos los puntos.

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..

4. Algoritmo en Python

El algoritmo para interpolación de Diferencias Divididas o Newton, considera reutilizar el procedimiento de cálculo de diferencias finitas incorporando la parte del denominador.

La creación de la expresión del polinomio también es semejante a la usada para diferencias finitas avanzadas.

Se incorpora la parte gráfica para observar los resultados en el intervalo xi, con el número de muestras = 101 para tener una buena resolución de la línea del polinomio.

# Diferencias Divididas de Newton -Interpolación
# Tarea: Verificar tamaño de vectores,
import numpy as np
import sympy as sym

# INGRESO
xi = [3.2 , 3.8 , 4.2 , 4.5 ]
fi = [5.12, 6.42, 7.25, 6.85]

# PROCEDIMIENTO
casicero = 1e-15  # redondear a cero
# Matrices como arreglo, numeros reales
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
n = len(xi)

# Tabla de Diferencias Divididas
tabla_etiq = ['i   ','xi  ','fi  ']
ki = np.arange(0,n,1) # filas
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)
n,m = np.shape(tabla)
# Calcula tabla de Diferencias Divididas
diagonal = n-1 # derecha a izquierda
j = 3  # inicia en columna 3
while (j < m): # columna
    tabla_etiq.append('F['+str(j-2)+']') # título columna
    i = 0 # cada fila de columna
    paso = j-2 # inicia en 1
    while (i < diagonal): # antes de diagonal
        tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1]

        denominador = (xi[i+paso]-xi[i])
        tabla[i,j] = tabla[i,j]/denominador

        if abs(tabla[i,j])<casicero: # casicero revisa
            tabla[i,j]=0
        i = i + 1
    diagonal = diagonal - 1
    j = j + 1
    
dDividida = tabla[0,3:] # diferencias Divididas

# polinomio con diferencias Divididas de Newton
x = sym.Symbol('x')
polinomio = fi[0] +0*x # en Sympy
for i in range(1,n,1):
    factor = dDividida[i-1]
    termino = 1
    for j in range(0,i,1):
        termino = termino*(x-xi[j])
    polinomio = polinomio + termino*factor

polisimple = polinomio.expand() # simplifica los (x-xi)
px = sym.lambdify(x,polisimple) # evaluación numérica

# SALIDA
np.set_printoptions(precision = 4)
print('Tabla Diferencia Dividida-Newton')
print([tabla_etiq])
print(tabla)
print('dDividida: ')
print(dDividida)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)

El resultado del algoritmo se muestra a continuación:

Tabla Diferencia Dividida-Newton
[['i   ', 'xi  ', 'fi  ', 'F[1]', 'F[2]', 'F[3]', 'F[4]']]
[[ 0.      3.2     5.12    2.1667 -0.0917 -3.6749  0.    ]
 [ 1.      3.8     6.42    2.075  -4.869   0.      0.    ]
 [ 2.      4.2     7.25   -1.3333  0.      0.      0.    ]
 [ 3.      4.5     6.85    0.      0.      0.      0.    ]]
dDividida: 
[ 2.1667 -0.0917 -3.6749  0.    ]
polinomio: 
2.16666666666667*x - 3.67490842490842*(x-4.2)*(x-3.8)*(x-3.2)
 - 0.0916666666666694*(x - 3.8)*(x - 3.2) - 1.81333333333334
polinomio simplificado: 
-3.67490842490842*x**3 + 41.0673076923077*x**2 
- 149.920860805861*x + 184.756923076923
>>>

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..

5. Gráfica de polinomio de interpolación

# GRAFICA  --------------
import matplotlib.pyplot as plt

titulo = 'Interpolación: Diferencias Divididas - Newton'
muestras = 21  # resolución gráfica

a = np.min(xi) # intervalo [a,b]
b = np.max(xi)
xk = np.linspace(a,b,muestras)
yk = px(xk)

plt.plot(xi,fi,'o', label='[xi,fi]')
plt.plot(xk,yk, label='p(x)')

try: # existen mensajes de error
    msj_existe = len(msj)
except NameError:
    msj = []
if len(msj)>0: # tramos con error
    untipo = msj[0][0]
    donde = msj[0][1] # indice error
    plt.plot(xi[donde:donde+2],fi[donde:donde+2],
             'ro',label=untipo)
    plt.plot(xi[donde:donde+2],fi[donde:donde+2],
             'r--')

plt.xlabel('xi')
plt.ylabel('fi')
plt.legend()
plt.title(titulo)
plt.show()

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]
..

6. Algoritmo como función

Se reordena el algoritmo para usar funciones, la gráfica es la misma que para el algoritmo sin funciones anterior

El bloque de salida es semejante al resultado anterior.

# Diferencias Divididas de Newton - Interpolación
# funciones diferencias_tabla
# Tarea: Verificar tamaño de vectores
import numpy as np
import math
import sympy as sym

def diferencias_tabla(xi,fi,tipo='finitas', vertabla=False,
                casicero = 1e-15, precision=4):
    '''Genera la tabla de diferencias finitas o divididas
      tipo = 'finitas, tipo = 'divididas'
    resultado en: tabla, titulo
    Tarea: verificar tamaño de vectores
    '''
    # revisa tipo de tabla
    tipolist = ['finitas','divididas']
    if not(tipo in tipolist):
        print('error de tipo, seleccione:',tipolist)
        return()
    
    prefijo = ['d','f']
    if tipo=='divididas':
        prefijo = ['F[',']']
    
    # Matrices como arreglo, numeros reales
    xi = np.array(xi,dtype=float)
    fi = np.array(fi,dtype=float)
    n = len(xi)

    # Tabla de Diferencias Finitas/Divididas
    tabla_etiq = ['i','xi','fi']
    ki = np.arange(0,n,1) # filas
    tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
    tabla = np.transpose(tabla)
    dfinita = np.zeros(shape=(n,n),dtype=float)
    tabla = np.concatenate((tabla,dfinita), axis=1)
    n,m = np.shape(tabla)
    # Calular tabla de Diferencias Finitas/Divididas
    diagonal = n-1 # derecha a izquierda
    j = 3  # inicia en columna 3
    while (j < m): # columna
        tabla_etiq.append(prefijo[0]+str(j-2)+prefijo[1])
        # paso = j-2 # inicia en 1
        i = 0 # fila
        while (i < diagonal): # antes de diagonal
            tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1]

            if tipo=='divididas':
                # denominador = xi[i+paso]-xi[i]
                denominador = xi[i+j-2]-xi[i]
                tabla[i,j] = tabla[i,j]/denominador
                
            if abs(tabla[i,j])<casicero: # casicero revisa
                    tabla[i,j]=0
            i = i + 1
        diagonal = diagonal - 1
        j = j + 1
            
    if vertabla==True:
        np.set_printoptions(precision)
        print('Tabla de Diferencias',tipo)
        print([tabla_etiq])
        print(tabla)
    return([tabla, tabla_etiq])

# PROGRAMA ---------------------

# INGRESO
xi = [3.2, 3.8, 4.2, 4.5]
fi = [5.12, 6.42, 7.25, 6.85]

tipo_tabla = 'divididas'

# PROCEDIMIENTO
casicero = 1e-12
# Vectores como arreglo, numeros reales
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
n = len(xi)

tabla,tabla_etiq = diferencias_tabla(xi,fi,
                        tipo=tipo_tabla,
                        vertabla=True,casicero = casicero)

dfinita = tabla[0,3:] # diferencias divididas
h = xi[1] - xi[0]     # suponer tramos equidistantes

# polinomio con diferencias Finitas Avanzadas/ divididas
x = sym.Symbol('x')
polinomio = fi[0] +0*x # sym.S.Zero en Sympy
for i in range(1,n,1):
    factor = dfinita[i-1] # diferencias divididas
    if tipo_tabla=='finitas': # diferencias Finitas Avanzadas
        denominador = math.factorial(i)*(h**i)
        factor = factor/denominador
    termino = 1
    for j in range(0,i,1):
        termino = termino*(x-xi[j])
    polinomio = polinomio + termino*factor

polisimple = polinomio.expand() # simplifica los (x-xi)
px = sym.lambdify(x,polisimple) # evaluacion numerica

# SALIDA
print('d'+tipo_tabla+': ')
print(dfinita)
print('Tramo h:',h)
print('polinomio: ')
#print(polinomio)
terminos = sym.Add.make_args(polinomio)
n_term = len(terminos)
for i in range(0,n_term,1):
    if i<(n_term-1):
        print(terminos[i],'+')
    else:
        print(terminos[i])
print()
print('polinomio simplificado: ' )
print(polisimple)

La gráfica se realiza con el bloque de la sección anterior

[ Dif_Divididas_Newton] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ gráfica ]
[ función ]