[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
1. Cuadratura de Gauss
Referencia: Chapra 22.3 p655, Rodríguez 7.3 p294, Burden 4.7 p168
La cuadratura de Gauss aproxima el integral de una función en un intervalo [a,b] centrado en cero mediante un cálculo numérico con menos operaciones y evaluaciones de la función. Se representa como una suma ponderada:
I \cong \Big( \frac{b-a}{2} \Big)\Big(c_0f(x_a) + c_1f(x_b)\Big)para la fórmula de dos puntos con referencia a una función centrada en cero y ancho unitario a cada lado, se tiene:
c_0 = c_1 = 1, x_0 = -\frac{1}{\sqrt{3}}, x_1 = \frac{1}{\sqrt{3}}Para un intervalo de evaluación desplazado en el eje x se requiere convertir los puntos al nuevo intervalo. Se desplaza el punto cero al centro del intervalo [a,b] y se corrige el desplazamiento hacia la izquierda y derecha del centro con x0 y x1.
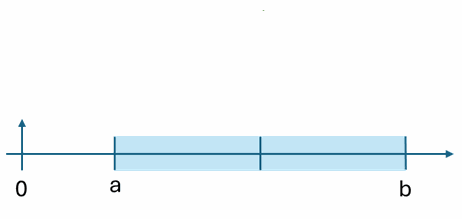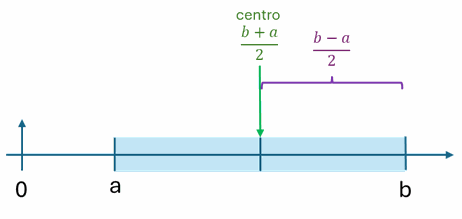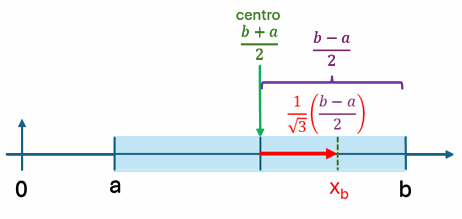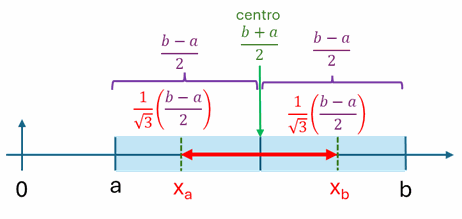
x_a = \frac{b+a}{2} - \frac{b-a}{2}\Big(\frac{1}{\sqrt{3}} \Big) x_b = \frac{b+a}{2} + \frac{b-a}{2}\Big(\frac{1}{\sqrt{3}} \Big)con lo que el resultado aproximado del integral se convierte en:
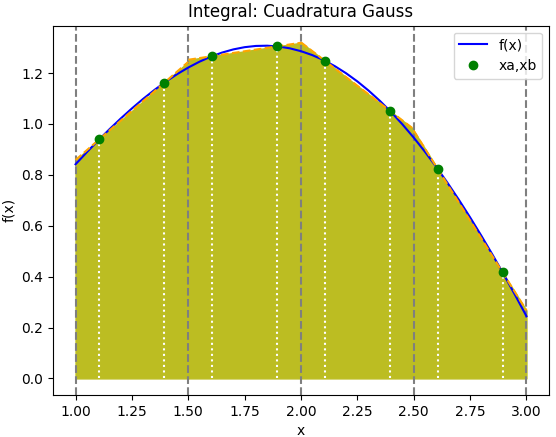
I \cong \frac{b-a}{2}(f(x_a) + f(x_b))cuya fórmula es semejante a una mejor aproximación de un trapecio, cuyos promedios de alturas son puntos internos de [a,b], concepto mostrado en la gráfica.
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
2. Ejercicio
Para el ejercicio y comparación de resultado con los otros métodos, se realiza el cálculo para un tramo en el intervalo [a,b].
\int_1^3 \sqrt{x} \sin(x) dx x_a = \frac{3+1}{2} - \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}}\Big)= 1.4226 x_b = \frac{3+1}{2} + \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}} \Big) = 2.5773 f(1.4226) = \sqrt{1.4226} \sin(1.4226) = 1.1796 f(2.5773) = \sqrt{2.5773} \sin(2.5773) = 0.8585con lo que el resultado aproximado del integral se convierte en:
I \cong \frac{3-1}{2}(1.1796 + 0.8585) = 2.0382que usando instrucciones de Python para obtener los valores:
>>> import numpy as np >>> (3+1)/2-(3-1)/2*(1/np.sqrt(3)) 1.4226497308103743 >>> (3+1)/2+(3-1)/2*(1/np.sqrt(3)) 2.5773502691896257 >>> fx = lambda x: np.sqrt(x)*np.sin(x) >>> fx(1.4226) 1.1796544827404145 >>> fx(2.5773) 0.8585957175067221 >>> ((3-1)/2)*(fx(1.4226)+fx(2.5773)) 2.0382
el resultado se puede mejorar aumentando el número de tramos en el intervalo [a,b]. Por ejemplo, el resultado usando 4 tramos el resultado es semejante al usar el método del trapecio con 128 tramos, lo que muestra el ahorro en cálculos entre los métodos
Integral: 2.05357719003 >>>
Concepto:
Ejercicio:
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
3. Algoritmo con Python
Para el ejercicio anterior, usando al 4 segmentos y en cada uno aplicando Cuadratura de Gauss, el integral resultante es:
Factores Gauss-Legendre puntos: 2 xgl: [-0.5773502691896258, 0.5773502691896258] cgl: [1.0, 1.0] tabla por intervalos [a,b] [a,b] : [1. 1.5] xi : [1.10566 1.39434] fi : [0.93979 1.16248] area : 0.5255697290782242 [a,b] : [1.5 2. ] xi : [1.60566 1.89434] fi : [1.26638 1.30494] area : 0.642828854689653 [a,b] : [2. 2.5] xi : [2.10566 2.39434] fi : [1.24843 1.05163] area : 0.5750145898962924 [a,b] : [2.5 3. ] xi : [2.60566 2.89434] fi : [0.82428 0.41638] area : 0.31016401636449004 Integral: 2.0535771900286597
Instrucciones en Python usando la Cuadratura de Gauss de dos puntos para una función f(x):
# Integración: Cuadratura de Gauss de 2 puntos # modelo con varios tramos entre [a,b] import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) a = 1 # intervalo de integración b = 3 tramos = 4 # subintervalos a integrar precision = 5 # decimales en tabla # PROCEDIMIENTO # cuadratura de 2 puntos n_puntos = 2 xgl = [-1/np.sqrt(3),1/np.sqrt(3)] cgl = [1.,1.] # cuadratura de n_puntos, fórmulas Gauss-Legendre #xgl, cgl = np.polynomial.legendre.leggauss(2) x_h = np.linspace(a,b,tramos+1) tabla = {} suma = 0 for k in range(0,tramos,1): a = x_h[k] b = x_h[k+1] centro = (a+b)/2 mitad = (b-a)/2 xa = centro + xgl[0]*mitad xb = centro + xgl[1]*mitad area = ((b-a)/2)*(cgl[0]*fx(xa) + cgl[1]*fx(xb)) tabla[k]= {'[a,b]': np.array([a,b]), 'xi': np.array([xa,xb]), 'fi': np.array([fx(xa),fx(xb)]), 'area':area } suma = suma + area # SALIDA np.set_printoptions(precision) print('Factores Gauss-Legendre puntos:',n_puntos) print('xgl:',xgl) print('cgl:',cgl) print('tabla por intervalos [a,b]') for k in range(0,tramos,1): for entrada in tabla[k]: print(entrada,':',tabla[k][entrada]) print('Integral: ', suma)
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
4. Gráfica por tramos
La gráfica que complementa el resultado anterior, se realiza añadiendo las instrucciones presentadas a continuación.
Considere que la gráfica es útil con pocos tramos en el intervalo[a,b]
# GRAFICA ------------- # concepto con 'pocos' tramos/segmentos import matplotlib.pyplot as plt titulo = 'Cuadratura Gauss-Legendre puntos:'+str(n_puntos) a = np.min(x_h); b = np.max(x_h) muestras_k = tramos*10+1 # fx suave en grafico xk = np.linspace(a,b,muestras_k) fk = fx(xk) # tramos marcas de división for i in range(0,tramos+1,1): plt.axvline(x_h[i],linestyle='dashed', color='tab:gray') for k in range(0,tramos,1): xi = tabla[k]['xi'] fi = tabla[k]['fi'] for i in range(0,n_puntos,1): plt.vlines(xi[i],0,fi[i], linestyle='dotted', color='gray') plt.plot(xi[i],fi[i],'o',color='gray') if n_puntos>2: plt.fill_between(xk,0,fk,color='tab:olive') if n_puntos==2: # recta trapecio for k in range(0,tramos,1): xi = tabla[k]['xi'] fi = tabla[k]['fi'] df = (fi[1]-fi[0])/(xi[1]-xi[0]) # pendiente f0 = fi[0] + df*(x_h[k]-xi[0]) # en xi[i] f1 = fi[0] + df*(x_h[k+1]-xi[0]) # en xi[i+1] plt.fill_between([x_h[k],x_h[k+1]], 0,[f0,f1], color='tab:olive') plt.plot([x_h[k],x_h[k+1]],[f0,f1], linestyle='dashed',color='orange') # linea fx plt.plot(xk,fk, label='f(x)', color = 'blue') plt.title(titulo) plt.xlabel('x') plt.ylabel('f(x)') plt.legend() plt.tight_layout() plt.show()
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
5. Tabla Cuadratura de Gauss-Legendre para n puntos
Referencia: Chapra Tabla 22.1 p661, Burden 10Ed Tabla 4.12 p172
Para un integral con intervalo centrado en el origen.
I \cong c_0 f(x_0) + c_1f(x_1) + … + c_{n-1}f(x_{n-1})| Puntos | Factor de ponderación | Argumentos de la función | Error de truncamiento |
| 2 | c0 = 1.0000000 c1 = 1.0000000 |
x0 = - 0.577350269 x1 = 0.577350269 |
≅ f(4)(x ) |
| 3 | c0 = 0.5555556 c1 = 0.8888889 c2 = 0.5555556 |
x0 = - 0.774596669 x1 = 0.0 x2 = 0.774596669 |
≅ f(6)(x ) |
| 4 | c0 = 0.3478548 c1 = 0.6521452 c2 = 0.6521452 c3 = 0.3478548 |
x0 = - 0.861136312 x1 = - 0.339981044 x2 = 0.339981044 x3 = 0.861136312 |
≅f (8)(x ) |
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
6. Función en librería np.polynomial.legendre.leggauss para n_puntos
Referencia: np.polynomial.legendre.leggauss
Para obtener los valores de la tabla, se puede usar la librería Numpy.
import numpy as np # n_puntos Gauss-Legendre n_puntos = 2 xg, cg = np.polynomial.legendre.leggauss(n_puntos) print("xg",xg) print("cg",cg)
que presenta como resultado:
xg [-0.57735027 0.57735027] cg [1. 1.]
donde se puede obtener los valores de la tabla con mas puntos.
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
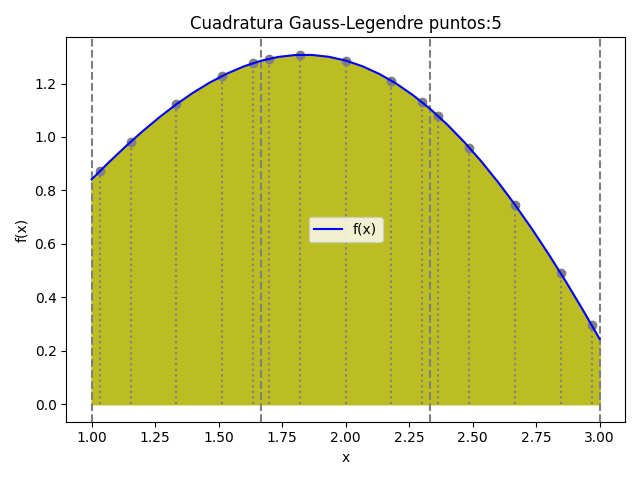
7. Algoritmo de Gauss-Legendre n_puntos
La gráfica se realiza con la sección gráfica anterior.
# Integración: Cuadratura de Gauss de n_puntos # modelo con varios tramos entre [a,b] import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) a = 1 # intervalo de integración b = 3 n_puntos = 5 # n_puntos>=2 tramos = 3 # subintervalos a integrar precision = 5 # decimales en tabla # PROCEDIMIENTO # cuadratura de n_puntos, fórmulas Gauss-Legendre xgl, cgl = np.polynomial.legendre.leggauss(n_puntos) x_h = np.linspace(a,b,tramos+1) # tramos tabla = {} suma = 0 for k in range(0,tramos,1): a = x_h[k] # intervalo[a,b] b = x_h[k+1] centro = (a+b)/2 mitad = (b-a)/2 xi=[]; fi=[]; suma_gl=0 for j in range(0,n_puntos,1): xj = centro + xgl[j]*mitad fj = fx(xj) suma_gl = suma_gl + cgl[j]*fj xi.append(xj) fi.append(fj) area = ((b-a)/2)*suma_gl tabla[k]= {'[a,b]': np.array([a,b]), 'xi': np.array(xi), 'fi': np.array(fi), 'area':area } suma = suma + area # SALIDA np.set_printoptions(precision) print('Factores Gauss-Legendre puntos:',n_puntos) print('xgl:',xgl) print('cgl:',cgl) print('tabla por intervalos [a,b]') for k in range(0,tramos,1): for entrada in tabla[k]: print(entrada,':',tabla[k][entrada]) print('Integral: ', suma)
resultado del algoritmo:
Factores Gauss-Legendre puntos: 5 xgl: [-0.90618 -0.53847 0. 0.53847 0.90618] cgl: [0.23693 0.47863 0.56889 0.47863 0.23693] tabla por intervalos [a,b] [a,b] : [1. 1.66667] xi : [1.03127 1.15384 1.33333 1.51282 1.63539] fi : [0.87127 0.98214 1.1223 1.2279 1.27616] area : 0.7350121364546989 [a,b] : [1.66667 2.33333] xi : [1.69794 1.82051 2. 2.17949 2.30206] fi : [1.29253 1.30741 1.28594 1.21116 1.12934] area : 0.8369414195585647 [a,b] : [2.33333 3. ] xi : [2.36461 2.48718 2.66667 2.84616 2.96873] fi : [1.07815 0.95996 0.74672 0.4912 0.29637] area : 0.4816765248057005 Integral: 2.053630080818964
La gráfica se realiza con la sección gráfica anterior.
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]