1. Tramos desiguales
Referencia: Chapra 21.3 p640
En la práctica, existen muchas situaciones con segmentos o tramos de tamaños desiguales. Por ejemplo, los datos obtenidos en experimentos frecuentemente son de este tipo. Para integración numérica, se busca identificar los segmentos de igual tamaño y aplicar: Simpson 3/8, Simpson 1/3 o trapecio.
El algoritmo se desarrolla al incorporar cada método como integral numérico de "fórmulas compuestas".
2. Ejercicio
Los datos de ejemplo son:
xi = [1. , 1.22222222, 1.44444444, 1.66666667,
1.88888889, 2.11111111, 2+1/3, 2+1/3+0.2,
2+1/3+0.4, 3. ]
fi = [0.84147098, 1.03905509, 1.19226953, 1.28506615,
1.30542157, 1.24598661, 1.10453193, 0.90952929,
0.65637234, 0.24442702]3. Algoritmo como función en Python
Los resultados del algoritmo muestran los detalles parciales al aplicar cada método acorde a los requisitos de cada uno en el siguiente orden: Tres tramos iguales permiten aplicar Simpson de 3/8, Dos tramos iguales permiten aplicar Simpson de 1/3, Un tramo desigual le aplica trapecio.
Los métodos usados de identifican por el arreglo de tramos iguales:
Fórmulas compuestas, tramos: 9
métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado
tramos iguales en xi: [3 0 0 3 0 0 2 0 1 0]
Simpson 3/8 : 0.7350425751495739
Simpson 3/8 : 0.8369852099634817
Simpson 1/3 : 0.3599347620000003
trapecio : 0.1201065813333333
tramos iguales en xi: [3 0 0 3 0 0 2 0 1 0]
Integral: 2.0520691284463894
Instrucciones en Python
# Integración Simpson 3/8, Simpson 1/3 y trapecio
# tramos no iguales, formulas compuestas
import numpy as np
# INGRESO
xi = [1. , 1.22222222, 1.44444444,
1.66666667, 1.88888889, 2.11111111,
2+1/3, 2+1/3+0.2, 2+1/3+0.4, 3. ]
fi = [0.84147098, 1.03905509, 1.19226953,
1.28506615, 1.30542157, 1.24598661,
1.10453193, 0.90952929, 0.65637234,
0.24442702]
# PROCEDIMIENTO
def simpson_compuesto(xi,fi,vertabla=False,
casicero=1e-7):
'''Método compuesto Simpson 3/8, Simpson 1/3 y trapecio
salida: integral,cuenta_h
'''
# vectores como arreglo, numeros reales
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
n = len(xi)
# Método compuesto Simpson 3/8, Simpson 1/3 y trapecio
cuenta_h = (-1)*np.ones(n,dtype=int) # sin usar
suma = 0 # integral total
suma_parcial =[] # integral por cada método
i = 0
while i<(n-1): # i<tramos, al menos un tramo
tramo_usado = False
h = xi[i+1]-xi[i] # tamaño de paso, supone constante
# tres tramos iguales
if (tramo_usado==False) and (i+3)<n:
d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos
errado = np.max(np.abs(d2x))
if errado<casicero: # Simpson 3/8
S38 = (3/8)*h*(fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3])
suma = suma + S38
cuenta_h[i:i+3] = [3,0,0] # Simpson 3/8
suma_parcial.append(['Simpson 3/8',S38])
i = i+3
tramo_usado = True
# dos tramos iguales
if (tramo_usado==False) and (i+2)<n:
d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos
errado = np.max(np.abs(d2x))
if errado<casicero: # Simpson 1/3
S13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2])
suma = suma + S13
cuenta_h[i:i+2] = [2,0]
suma_parcial.append(['Simpson 1/3',S13])
i = i+2
tramo_usado = True
# un tramo igual
if (tramo_usado == False) and (i+1)<n:
trapecio = (h/2)*(fi[i]+fi[i+1])
suma = suma + trapecio
cuenta_h[i:i+1] = [1] # usar trapecio
suma_parcial.append(['trapecio',trapecio])
i = i+1
tramo_usado = True
cuenta_h[n-1] = 0 # ultima casilla
if vertabla==True: #mostrar datos parciales
print('Fórmulas compuestas, tramos:',n-1)
print('métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado')
print('tramos iguales en xi:',cuenta_h)
for unparcial in suma_parcial:
print('',unparcial[0],':',unparcial[1])
return(suma,cuenta_h)
# usa función
area,cuenta_h = simpson_compuesto(xi,fi,vertabla=True)
# SALIDA
print('tramos iguales en xi:',cuenta_h)
print('Integral:',area)
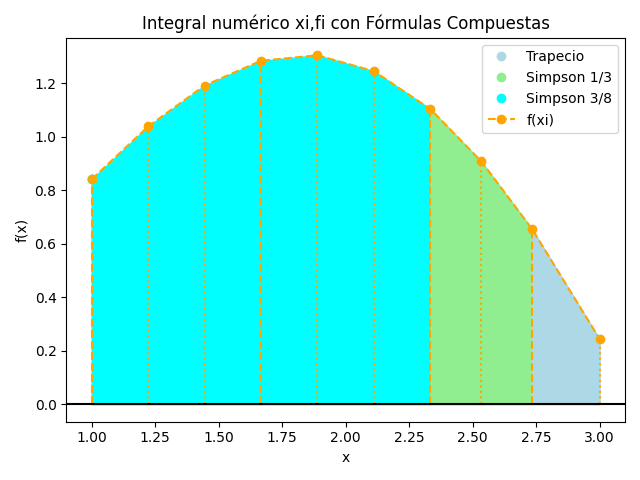
4. Gráfica de segmentos desiguales
En la gráfica se diferencian los métodos aplicados por colores.
Se añaden al algoritmo anterior las siguientes instrucciones,
# GRAFICA ---------------------
import matplotlib.pyplot as plt
n = len(xi) # muestras
tramos = n-1
metodotipo = [['na','grey'],
['Trapecio','lightblue'],
['Simpson 1/3','lightgreen'],
['Simpson 3/8','cyan']]
# etiquetas linea
plt.plot(xi[0],fi[0],'o', label=metodotipo[1][0],
color=metodotipo[1][1])
plt.plot(xi[0],fi[0],'o', label=metodotipo[2][0],
color=metodotipo[2][1])
plt.plot(xi[0],fi[0],'o', label=metodotipo[3][0],
color=metodotipo[3][1])
# relleno y bordes
tipo = 0
for i in range(0,tramos,1):
if cuenta_h[i]>0:
tipo = cuenta_h[i]
plt.fill_between([xi[i],xi[i+1]],
[fi[i],fi[i+1]],[0,0],
color=metodotipo[tipo][1])
# Divisiones entre tramos
for i in range(0,n,1):
tipolinea = 'dashed' # inicia un método
if cuenta_h[i]==0:
tipolinea = 'dotted' # dentro de un método
plt.vlines(xi[i],0,fi[i],linestyle=tipolinea,
color='orange')
# puntos de xi,fi
plt.plot(xi,fi,marker='o',linestyle='dashed',
color='orange',label='f(xi)')
plt.axhline(0,color='black') # eje x
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Integral numérico xi,fi con Fórmulas Compuestas')
plt.legend()
plt.tight_layout()
plt.show()
5. Diferencias entre tramos xi
Las diferencias entre tramos pueden ser analizadas con una gráfica, usando operaciones de diferencias finitas.
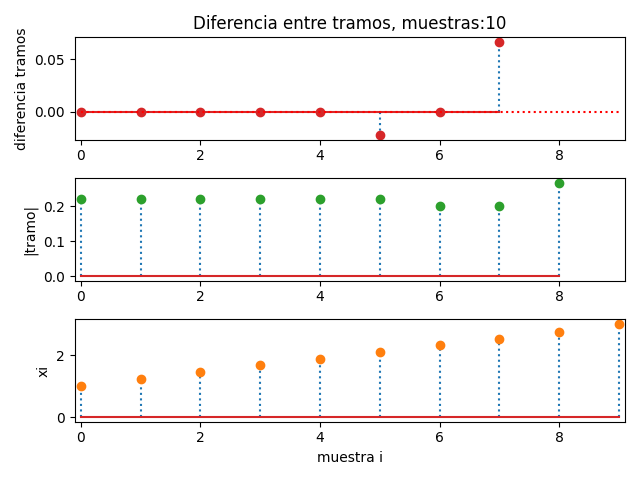
Resultado del algoritmo:
d1xi: [0.22222222 0.22222222 0.22222223 0.22222222
0.22222222 0.22222222 0.2 0.2
0.26666667]
d2xi: [ 2.22044605e-16 9.99999972e-09 -9.99999972e-09
-2.22044605e-16 3.33333361e-09 -2.22222233e-02
-4.44089210e-16 6.66666667e-02]
diferencia máxima: 4.440892098500626e-16 en i: 7
tramos iguales en xi: [3 0 0 2 0 1 2 0 1 0]Instrucciones en Python
# revisa xi por
# tramos equidistantes y no iguales
import numpy as np
# INGRESO
xi = [1. , 1.22222222, 1.44444444, 1.66666667,
1.88888889, 2.11111111, 2+1/3, 2+1/3+0.2,
2+1/3+0.4, 3. ]
# PROCEDIMIENTO
casicero=1e-7
# vectores como arreglo, números reales
xi = np.array(xi,dtype=float)
n = len(xi)
# diferencias finitas en xi
d1xi = np.diff(xi,1) # magnitud de tramos
d2xi = np.diff(xi,2) # diferencia entre tramos
errado = np.max(np.abs(d2xi)) # error mayor
donde = np.argmax(np.abs(d2xi)) # donde es error mayor
# revisa tramos iguales
cuenta_h = -1*np.ones(n,dtype=int)
i = 0
while i<(n-1): # i<tramos, al menos un tramo
tramo_usado = False
# tres tramos iguales
if (tramo_usado==False) and (i+3)<n:
d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos
errado = np.max(np.abs(d2x))
if errado<casicero: # Simpson 3/8
cuenta_h[i:i+3] = [3,0,0]
i = i+3
tramo_usado==True
# dos tramos iguales
if (tramo_usado==False) and (i+2)<n:
d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos
errado = np.max(np.abs(d2x))
if errado<casicero: # Simpson 1/3
cuenta_h[i:i+2] = [2,0]
i = i+2
tramo_usado = True
# un tramo igual
if (tramo_usado == False) and (i+1)<n:
cuenta_h[i:i+1] = [1] # usar trapecio
i = i+1
tramo_usado = True
cuenta_h[n-1] = 0 # ultima casilla
# SALIDA
print('d1xi:',d1xi)
print('d2xi:',d2xi)
print('diferencia máxima:',errado,' en i:',donde)
print('tramos iguales en xi:',cuenta_h)
# GRAFICA
import matplotlib.pyplot as plt
m = len(xi)-1
plt.subplot(311) # diferencia entre tramos
plt.stem(d2xi,linefmt=':',markerfmt ='C03')
plt.plot(np.ones(n)*casicero,color='red',linestyle='dotted')
plt.xlim(-0.1,m+0.1)
plt.ylabel('diferencia tramos')
plt.title('Diferencia entre tramos, muestras:'+str(n))
plt.subplot(312) # tramos
plt.stem(d1xi,linefmt=':',markerfmt ='C02')
plt.xlim(-0.1,m+0.1)
plt.ylabel('|tramo|')
plt.subplot(313) # muestras
plt.stem(xi,linefmt=':',markerfmt ='C01')
plt.xlim(-0.1,m+0.1)
plt.ylabel('xi')
plt.xlabel('muestra i')
plt.tight_layout()
plt.show()