1. EDO \frac{\delta y}{\delta x} Runge-Kutta 4to Orden
Referencia: Chapra 25.3.3 p746, Rodríguez 9.1.8 p358
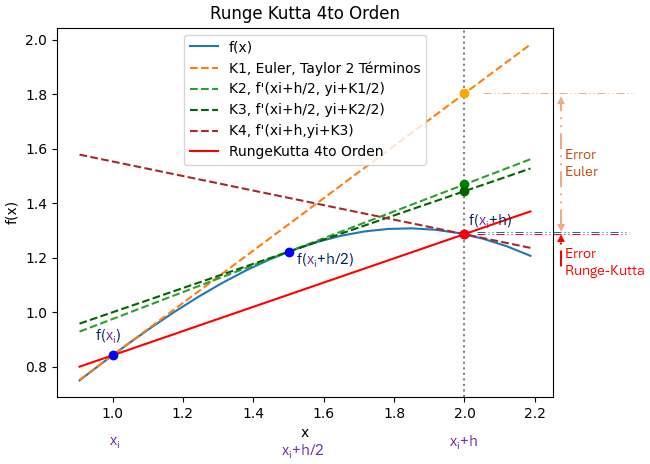
Para una ecuación diferencial de primera derivada (primer orden) con una condición de inicio:
\frac{\delta y}{\delta x} + etc =0 y'(x) = f(x_i,y_i) y(x_0) = y_0La fórmula de Runge-Kutta de 4to orden realiza una corrección con 4 valores de K:
y_{i+1} = y_i + \frac{K_1 + 2K_2 + 2K_3 + K_4}{6}debe ser equivalente a la serie de Taylor de 5 términos:
y_{i+1} = y_i + h f(x_i,y_i) + + \frac{h^2}{2!} f'(x_i,y_i) + \frac{h^3}{3!} f''(x_i,y_i) + +\frac{h^4}{4!} f'''(x_i,y_i) + O(h^5) x_{i+1} = x_i + hRunge-Kutta 4do Orden tiene error de truncamiento O(h5)
2. Ejercicio
Para el desarrollo analítico se tienen las siguientes expresiones para el ejercicio usado en Runge-Kutta de orden 2, que ahora será con orden 4:
f(x,y) = y' = y -x^2 +x +1Se usa las expresiones de Runge-Kutta en orden, K1 corresponde a una corrección de EDO con Taylor de dos términos (método de Euler). K2 considera el cálculo a medio tamaño de paso más adelante.
iteración:
K_1 = h f(x_i,y_i) = 0.1 (y_i -x_i^2 +x_i +1) K_2 = h f\Big(x_i+\frac{h}{2}, y_i + \frac{K_1}{2} \Big) K_2 = 0.1 \Big(\big(y_i+\frac{K_1}{2}\big) -\big(x_i+\frac{h}{2}\big)^2 +\big(x_i+\frac{h}{2}\big) +1 \Big) K_3 = h f\Big(x_i+\frac{h}{2}, y_i + \frac{K_2}{2} \Big) K_3 = 0.1 \Big(\big(y_i+\frac{K_2}{2}\big) -\big(x_i+\frac{h}{2}\big)^2 +\big(x_i+\frac{h}{2}\big) +1 \Big) K_4 = h f(x_i+h, y_i + K_3 ) K_4 = 0.1 \Big((y_i+K_3) -(x_i+h)^2 +(x_i+h) +1 \Big) y_{i+1} = y_i + \frac{K_1+2K_2+2K_3+K_4}{6} x_{i+1} = x_i + hLas iteraciones se dejan como tarea
3. Algoritmo en Python como Función
def rungekutta4(d1y,x0,y0,h,muestras, vertabla=False, precision=6):
''' solucion a EDO con Runge-Kutta 4do Orden primera derivada,
x0,y0 son valores iniciales, tamaño de paso h.
muestras es la cantidad de puntos a calcular.
'''
# Runge Kutta de 4do orden
tamano = muestras + 1
tabla = np.zeros(shape=(tamano,2+4),dtype=float)
# incluye el punto [x0,y0,K1,K2,K3,K4]
tabla[0] = [x0,y0,0,0,0,0]
xi = x0
yi = y0
for i in range(1,tamano,1):
K1 = h * d1y(xi,yi)
K2 = h * d1y(xi+h/2, yi + K1/2)
K3 = h * d1y(xi+h/2, yi + K2/2)
K4 = h * d1y(xi+h, yi + K3)
yi = yi + (1/6)*(K1+2*K2+2*K3 +K4)
xi = xi + h
tabla[i] = [xi,yi,K1,K2,K3,K4]
if vertabla==True:
np.set_printoptions(precision)
titulo = ' [xi, yi, K1, K2, K3, K4 ]'
print(' EDO con Runge-Kutta 4do Orden primera derivada')
print(titulo)
print(tabla)
return(tabla)
Note que el método de Runge-Kutta de 4to orden es similar a la regla de Simpson 1/3. La ecuación representa un promedio ponderado para establecer la mejor pendiente.
4. Ejercicio en video
2Eva2018TI_T1 Paracaidista wingsuit
Solución Propuesta: s2Eva2018TI_T1 Paracaidista wingsuit
https://youtu.be/c1_vQRhl8Rg
La segunda parte corresponde a Runge-Kutta de 4to Orden